Magneto Static: solved equations (scalar model)
Introduction
The scalar model is a general model proposed for 3D applications.
This model is used by default (automatically) by the 3D solver of Flux 3D to solve 3D applications.
Equation solved in the scalar model (3D)
The equation ![]() allows
introducing different magnetic scalar potentials ϕ, such as:
allows
introducing different magnetic scalar potentials ϕ, such as: ![]() . The term
. The term ![]() is the non-rotational part
of the field
is the non-rotational part
of the field ![]() (
( ![]() ), while the term
), while the term ![]() can be rotational or
null.
can be rotational or
null.
![]() can be chosen in
different ways and a different choice of
can be chosen in
different ways and a different choice of ![]() leads to
a different scalar potentials. Flux 3D has different magnetic
formulations that use different scalar potentials. To each region
of the problem a formulation is associated and, consequently, an
equation.
leads to
a different scalar potentials. Flux 3D has different magnetic
formulations that use different scalar potentials. To each region
of the problem a formulation is associated and, consequently, an
equation.
The general form of the equation solved in scalar model by the finite elements method in a magnetostatic application is written:
![]()
where:
- [μr] is the tensor of the relative permeability of the medium
- μ0 is the permeability of the vacuum; μ0 = 4 π 10-7 (in H/m)
- ϕ is a magnetic scalar potential (in A); there are two potentials written ϕtot and ϕred
-
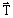 is a term
corresponding to sources
is a term
corresponding to sources(field source or electric vector potential (in A/m)
-
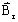 is the remanent
magnetic flux (permanent magnets) (in T)
is the remanent
magnetic flux (permanent magnets) (in T)
The proposed formulations…
The three formulations proposed in the scalar model correspond schematically to the following three situations:
- there are no current sources
- the current sources are of non-meshed type
- the current sources are of meshed type
The solved equations in these three situations are presented below.
Separately used, each of these formulations has significant limitations; used in a coupled manner, they form an efficient general model.
The scalar total potential (3D)
The total magnetic scalar potential , ϕtot, is used when there are no current
sources. The current density ![]() is null. This case corresponds to
is null. This case corresponds to ![]() in the general equation of
the scalar model.
in the general equation of
the scalar model.
The intensity of the magnetic field ![]() has the expression:
has the expression: ![]()
and the solved equation is: ![]()
The state variable is the total magnetic scalar potential: ϕtot
This variable is written V1 in Flux.
The reduced scalar potential with respect to Hj (3D)
The reduced magnetic scalar potential with respect to Hj,
ϕredHj, is used when the current sources are of the non-meshed
type. This case corresponds to ![]() in the general equation of the scalar model, with Hj
analytically computed by the Biot and Savart formula (see § Magneto Static: non-meshed sources (3D specific) ).
in the general equation of the scalar model, with Hj
analytically computed by the Biot and Savart formula (see § Magneto Static: non-meshed sources (3D specific) ).
The magnetic field strength ![]() has the
expression:
has the
expression: ![]()
and the solved equation: ![]()
The state variable is the total magnetic scalar potential with respect to Hj: ϕredHj
This variable is written V1R in Flux.
The reduced scalar potential with respect to T0 (3D)
The reduced magnetic scalar potential with respect to T0,
ϕredTo, is used when the current sources are of the meshed type.
This case corresponds to ![]() in the general equation of the scalar model. The quantity
in the general equation of the scalar model. The quantity ![]() satisfies the relation
satisfies the relation
![]() , where
, where ![]() is the current density in
the meshed region of field sources.
is the current density in
the meshed region of field sources.
The magnetic field strength ![]() has the
expression:
has the
expression: ![]()
and the solved equation is: ![]()
Thus, the state variables are:
-
the reduced magnetic scalar potential with respect to T0: ϕredTo
This variable is also written V1R in Flux
- the electric vector potential
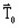 , variable non directly accessible in Flux
, variable non directly accessible in Flux