Viscous Heating Inside a Rotating Annulus

In this application, AcuSolve is used to simulate fluid flow and viscous heating in an annulus formed by concentric cylinders. AcuSolve results are compared with analytical results adapted from Bird and others (1960). The close agreement of AcuSolve results with analytical results validates the ability of AcuSolve to model cases with viscous heating.

Problem Description

The problem consists of a viscous fluid filling the annulus between two concentric cylinders, as shown in the following image, which is not drawn to scale. The inner cylinder has a radius of 1.0 m and is fixed in place. The outer cylinder has a radius of 2.0 m and rotates with a constant angular velocity of 0.5 rad/s. The inner cylinder is held at a constant temperature of 273 K and the outer cylinder is held at 274 K.

The rotation of the outer cylinder causes the fluid to rotate due to the viscous shearing near the wall. As the inner cylinder is fixed, a velocity gradient is generated as a function of distance from the inner cylinder center. Viscous stresses within the domain generate significant amounts of heat, leading to a substantial increase in the fluid temperature in regions of high shear.


Figure 1. Critical Dimensions and Parameters for Simulating Viscous Heating Inside a Rotating Annulus
The simulation was performed as a two-dimensional problem by constructing a volume mesh that contains a single layer of elements in the extruded direction, normal to the flow plane, and by imposing symmetry boundary conditions on the extruded planes.


Figure 2. Mesh used for Simulating Viscous Heating Inside a Rotating Annulus

AcuSolve Results

The AcuSolve solution converged to a steady state and the results reflect the mean flow conditions. Flow is induced by the viscous shearing near the outer wall, creating a velocity gradient with the highest velocity near the moving wall.


Figure 3. Contours of Velocity Magnitude (m/s)
The velocity gradient causes viscous heating, causing the fluid temperature to increase. The resulting temperature profile is nonlinear with the highest temperatures occurring in the space between the cylinders.


Figure 4. Contours of Temperature (K)
AcuSolve results were compared to analytical results for velocity and for temperature across a range of radial locations.


Figure 5. Velocity Magnitude Plotted Against Radial Location from the Center of the Inner Cylinder


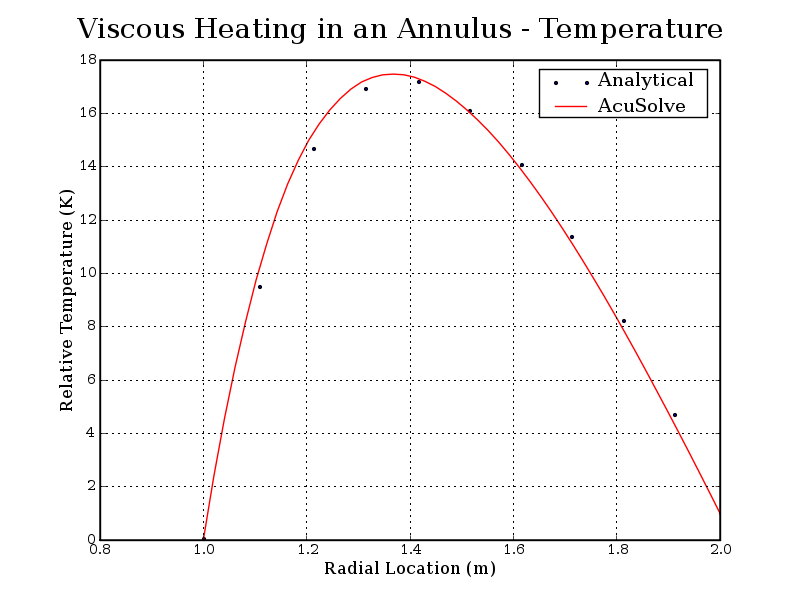
Figure 6. Temperature (Relative to the Inner Cylinder Wall Temperature) Plotted Against Radial Location from the Center of the Inner Pipe

Summary

The AcuSolve results compare well with the analytical results for both the flow field and the temperature across the annulus. In this application, flow is induced due to the viscous stresses generated by the rotation of the exterior cylinder. Velocity gradients between the cylinders give rise to shear stresses that induce frictional heating of the fluid. Due to the high viscosity of the fluid, the viscous heating is significant and leads to large increases in the temperature between the cylinders. This application validates the ability of AcuSolve to simulate flows where the viscous heating contribution is significant.

Simulation Settings for Viscous Heating Inside a Rotating Annulus

SimLab database file: <your working directory>\annulus_rotating_heat\annulus_rotating_heat.slb

Global

  • Problem Description
    • Analysis type - Steady State
    • Temperature equation - Advective Diffusive
    • Turbulence equation - Laminar
  • Auto Solution Strategy
    • Relaxation factor - 0.2
  • Material Model
    • Fluid
      • Density - 1.0 kg/m3
      • Viscosity - 300 kg/m-sec
      • Conductivity - 1.0 W/m-K
  • Reference Frame
    • Outer_Rotation
      • Angular Velocity
        • X-component - 0.0 rad/sec
        • Y-component - 0.0 rad/sec
        • Z-component - 0.5 rad/sec

    Model

  • Volumes
    • Fluid
      • Element Set
        • Material model - Fluid
        • Viscous heating - On
  • Surfaces
    • Inner_Cylinder
      • Simple Boundary Condition
        • Type - Wall
        • Temperature BC type - Value
        • Temperature - 273.0 K
    • Outer_Cylinder
      • Simple Boundary Condition
        • Type - Wall
        • Reference frame - Outer_Rotation
        • Temperature BC type - Value
        • Temperature - 274.0 K
    • Symm_MaxZ
      • Simple Boundary Condition
        • Type - Symmetry
    • Symm_MinZ
      • Simple Boundary Condition
        • Type - Symmetry
  • Nodes
    • Node 1
      • Pressure
        • Type - Zero

References

R. B. Bird, W. E. Stewart, and E. N. Lightfoot. "Transport phenomena". New York, John Wiley and Sons, 1960