ACU-T: 5403 Piezoelectric Flow Energy Harvester: A Fluid-Structure Interaction

This tutorial provides the instructions for setting up, solving and viewing results for a simulation of a piezoelectric fluid harvester. In this simulation, a piezoelectric flow harvester is placed in a fluid flow channel. The harvester is attached to a cylinder mount which also acts as a bluff body causing vortices in the fluid flow. The interaction between the pressure fields generated by the vortices and the flow harvester structure is simulated in this tutorial. AcuSolve is used in conjunction with a structural solver to compute the structural displacement of the harvester using a direct-coupled fluid structure interaction (DC-FSI) approach. Arbitrary Lagrangian Eulerian (ALE) approach is used to compute the mesh deformation in the fluid domain as it interacts with the deforming structure.

The basic steps in any CFD simulation are shown in ACU-T: 2000 Turbulent Flow in a Mixing Elbow. The PFSI approach for a fluid-structure multiphysics problem has been discussed in the Piezoelectric Flow Energy Harvester PFSI tutorial. The following additional capabilities of AcuSolve are introduced in this tutorial:
  • Set up a Direct Coupled FSI simulation (DC-FSI)
  • AcuSolve/OptiStruct multiphysics coupling
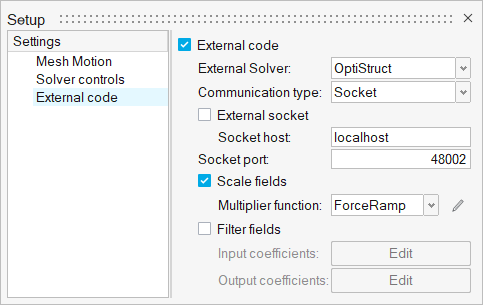
  • Setting up external code parameters to support coupling
  • Assigning external code parameters to surfaces
In this tutorial you will do the following:
  • Analyze the problem
  • Start HyperMesh CFD and create a simulation database
  • Import the mesh for the simulation.
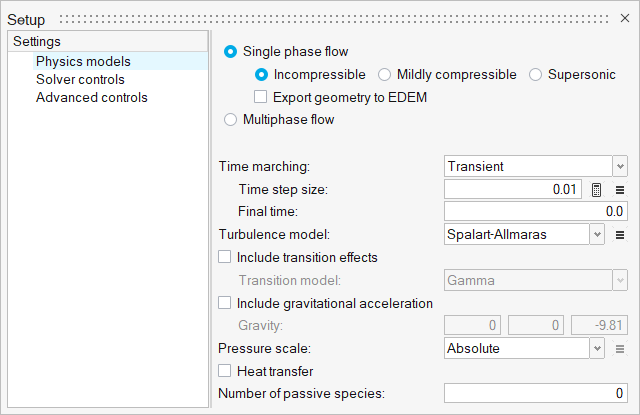
  • Set general problem parameters
  • Set the appropriate boundary conditions for the coupling surfaces
  • Run OptiStruct
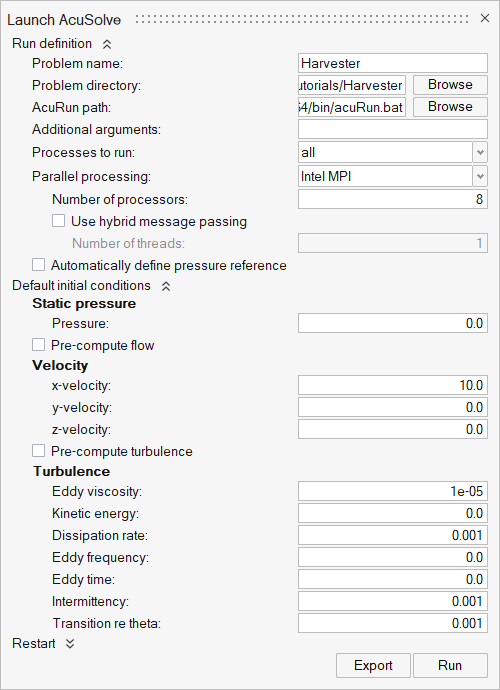
  • Run AcuSolve
  • Monitor the solution with HyperMesh CFD
  • Post-process the nodal output with HyperMesh CFD
  • Create an animation for the transient simulation with HyperMesh CFD Post

Prerequisites

You should have already run through the introductory tutorial, ACU-T: 2000 Turbulent Flow in a Mixing Elbow. It is assumed that you have some familiarity with HyperMesh CFD and AcuSolve. You will also need access to a licensed version of AcuSolve.

The coupled structural solver used for this tutorial is another product, OptiStruct. Thus, to follow this tutorial you will also need access to a licensed version of OptiStruct. The corresponding OptiStruct setup for this tutorial is available in the OptiStruct tutorial manual.

Before you begin, copy the file(s) used in this tutorial to your working directory.

The file ACU-T5403_Harvester_DCFSI.hm stores the geometry information for the fluid portion of the model for this problem, and the file slab_dcfsi.fem is the OptiStruct input deck for this problem.

The color of objects shown in the modeling window in this tutorial and those displayed on your screen may differ. The default color scheme in HyperMesh CFD is "random," in which colors are randomly assigned to groups as they are created. In addition, this tutorial was developed on Windows. If you are running this tutorial on a different operating system, you may notice a slight difference between the images displayed on your screen and the images shown in the tutorial.

Note: This tutorial does not cover the steps related to geometry cleanup and meshing.

Analyze the Problem

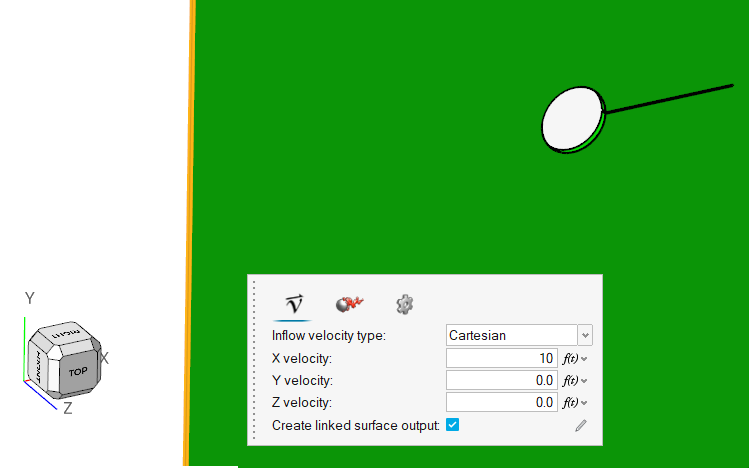
An important step in any CFD simulation is to examine the engineering problem at hand and determine the important parameters that need to be provided to AcuSolve. Parameters can be based on geometrical elements, such as inlets, outlets, or walls, and on flow conditions , such as fluid properties, velocity.

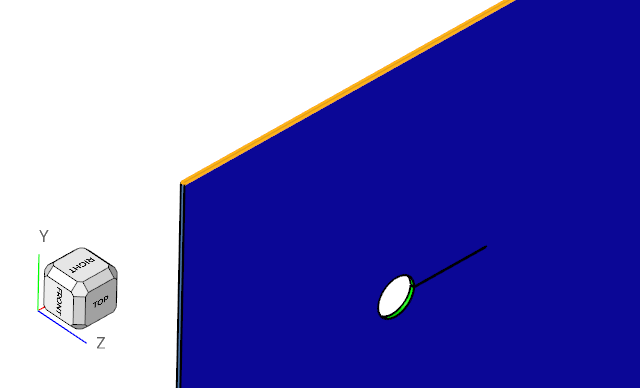
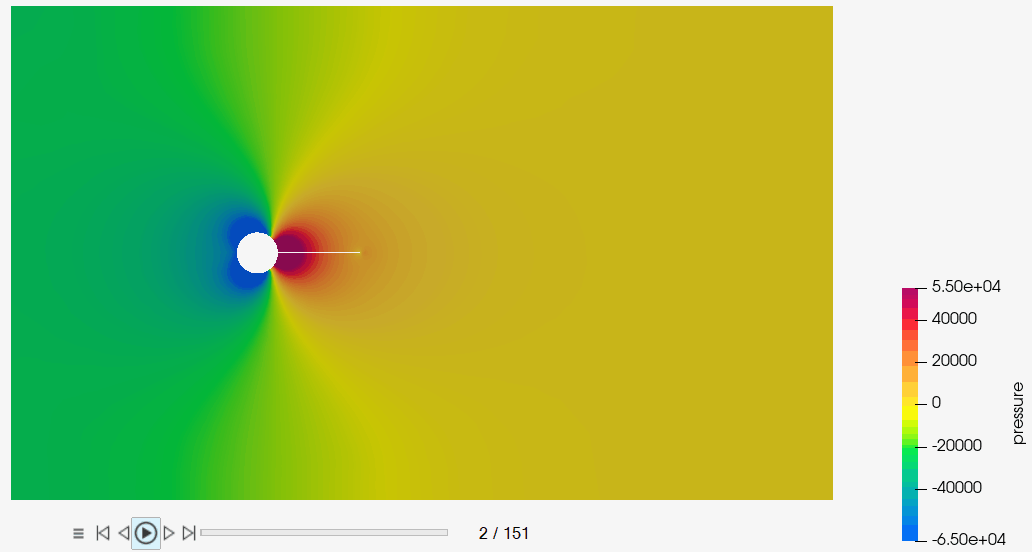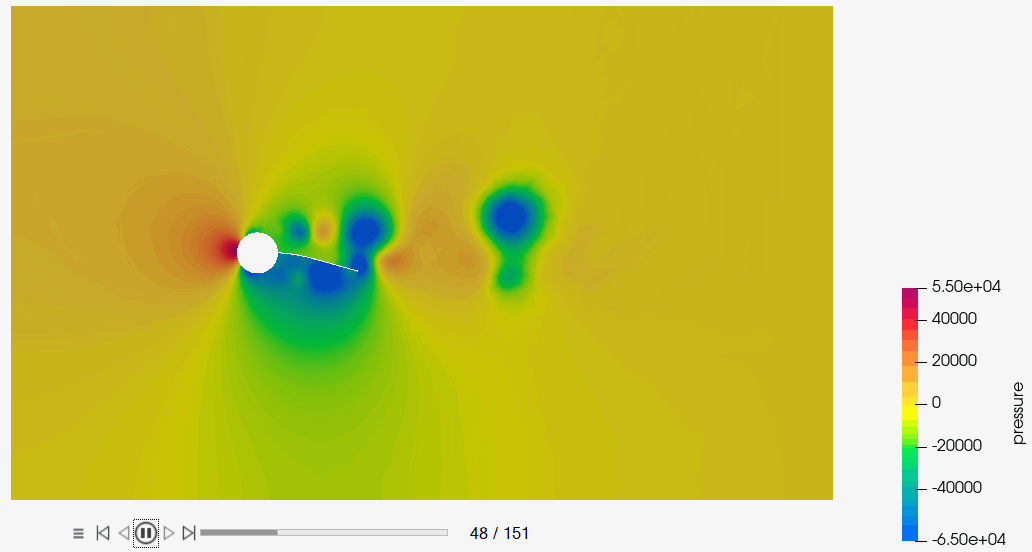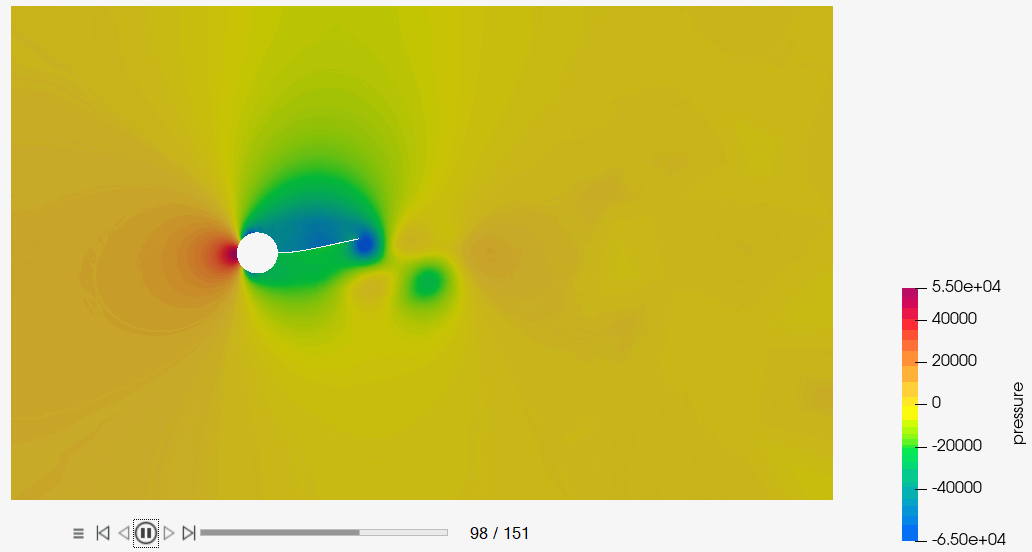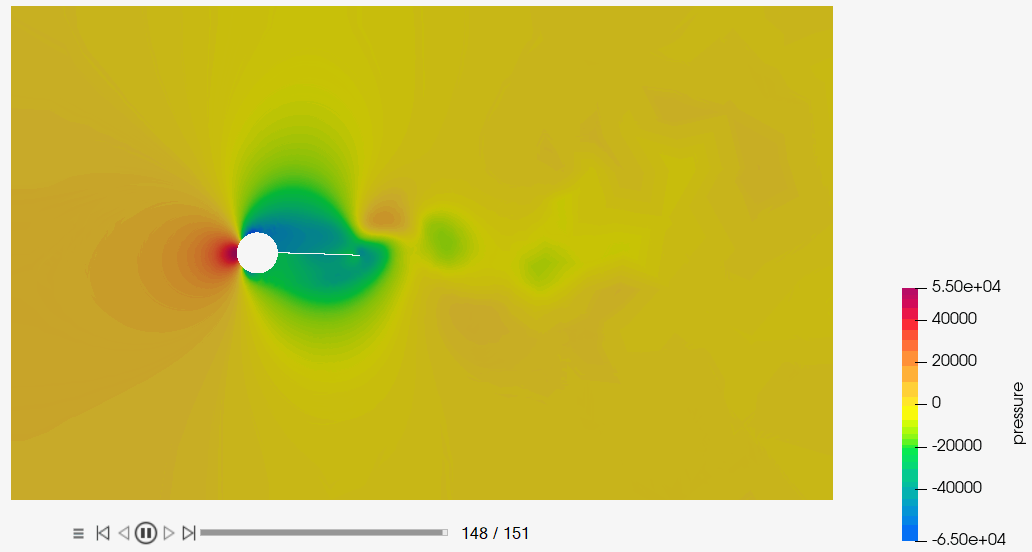
The schematics of the problem is shown in Figure 1. The CFD model consists of a cylindrical body and a cantilever beam. This cylindrical body generates vortex shedding. This vortex shedding creates a zone of alternating asymmetric pressure distribution on either side of the beam. Such an alternating pressure distribution exerts an oscillating force on the beam, creating a sustainable oscillating vibration in the beam.

The fluid solver does not require the solid body to be modeled. However, the structural solver will solve for the structural deformation using the fluid flow and pressure field which will be acting on the surface of the structure. The information required by the structural solver for structure displacement calculation will be passed on to it by the fluid solver. The structural solver on the other hand, will pass on the displacement information to the fluid solver. The fluid solver will then use this displacement information to calculate the flow field at the next time step, which will then be used by the structural solver to update the displacement information. This back and forth exchange of information between the fluid and structural solver will take place at each time step, and continue until one of the solvers signals the end of simulation. Figure 2 shows the arrangement of the beam with its various layers.



Figure 1. Schematic of the Problem


Figure 2. The Beam with its Various Layers

Fluid Structure Interaction

Fluid Structure Interaction is the interaction between a fluid flow and a deformable solid structure in contact with this flow. An FSI problem can be an external or an internal flow problem. The fluid flow can be external with the solid body immersed in the flow, for example, a windmill blade in open atmosphere. The fluid flow can also be internal with the solid body enclosing the flow, for example, fluid flow inside a deformable pipe. In both cases, the principle behind solving the problem remains the same. When a fluid flow encounters a structure, fluid pressure exerts a stress on the solid body that can lead to deformations in the structure. The magnitude of the deformation depends on the stiffness of the structure material and the magnitude of pressure force exerted by the fluid. The deformation in the structure shape then leads to altering of the flow characteristics in vicinity of the structure.

An FSI problem is thus a multiphysics problem, with the coupled laws of structural and fluid mechanics affecting the solution. There are two widely used approaches with which this coupling is achieved:
  1. Practical-FSI (P-FSI): The structure is reduced in the modal space and coupled to the fluid domain through interface nodes. The coupling between the solvers happens in a single pass itself. Structural behavior is limited to be linear in a P-FSI simulation.
  2. Direct coupling (DC-FSI): The coupling is a co-simulation between the structural and the fluid solver, with each solver stepping through time simultaneously and iterating to equilibrium in each time step.

In case the deformations in the structure are large enough to alter the fluid flow significantly, the DC-FSI co-simulation approach should be used. With this approach, as the fluid flow and pressure fields affect the structural deformations, and the structural deformations affect the flow and pressure, the information about these effects is exchanged between the solvers in real time.

Given the difference in coupling methodology, it is likely that slightly different results will be observed when a same problem is solved using P-FSI and DC-FSI approaches. The choice of the approach that should be used shall depend on the problem and the available resources. As mentioned above, the P-FSI approach should be limited to the cases when displacements in the structure are small, and the structural behavior can be approximated to be linear. For all other cases, DC-FSI should be preferred. However, DC-FSI simulations incur a higher computational resources cost. With this consideration, P-FSI simulation can also be used as a preliminary test simulation before a DC-FSI simulation is carried out.

FSI can be stable or oscillatory. In a stable FSI, the deformed shape of the structure will not change with time, unless the flow changes as well. In an oscillatory FSI, once the structure is deformed, it will try to return to its non-deformed state and then the whole deformation process repeats itself.

Mesh Motion Approaches in AcuSolve

Many simulations require deformation of the domain with time. AcuSolve provides two approaches for handling dynamic meshes:
  1. Arbitrary Lagrangian Eulerian (ALE)
  2. Interpolated Mesh Motion.

Arbitrary Lagrangian Eulerian (ALE)

ALE is an approach for mesh motion in which the computational nodes are moved arbitrarily with the aim of optimizing the element quality. An additional Partial Differential Equation (PDE) is solved to arrive at the appropriate mesh position. ALE is capable of handling complex arbitrary motions and is therefore the most general approach in simulating moving mesh problems. Generality comes with additional computational cost because of the extra PDE to be solved. For simpler motions like 1D or 2D motions faster approaches are available which include interpolated mesh motion, general specified motions, nodal boundary conditions based approaches.

Start HyperMesh CFD and Open the HyperMesh Database

  1. Start HyperMesh CFD from the Windows Start menu by clicking Start > Altair <version> > HyperMesh CFD.
  2. From the Home tools, Files tool group, click the Open Model tool.


    Figure 3.
    The Open File dialog opens.
  3. Browse to the directory where you saved the model file. Select the HyperMesh file ACU-T5403_Harvester_DCFSI.hm and click Open.
  4. Click File > Save As.
  5. Create a new directory named Harvester and navigate into this directory.
    This will be the working directory and all the files related to the simulation will be stored in this location.
  6. Enter Harvester as the file name for the database, or choose any name of your preference.
  7. Click Save to create the database.

Validate the Geometry

The Validate tool scans through the entire model, performs checks on the surfaces and solids, and flags any defects in the geometry, such as free edges, closed shells, intersections, duplicates, and slivers.

To focus on the physics part of the simulation, this tutorial input file contains geometry which has already been validated. Observe that a blue check mark appears on the top-left corner of the Validate icon on the Geometry ribbon. This indicates that the geometry is valid, and you can go to the flow set up.


Figure 4.

Set Up Flow

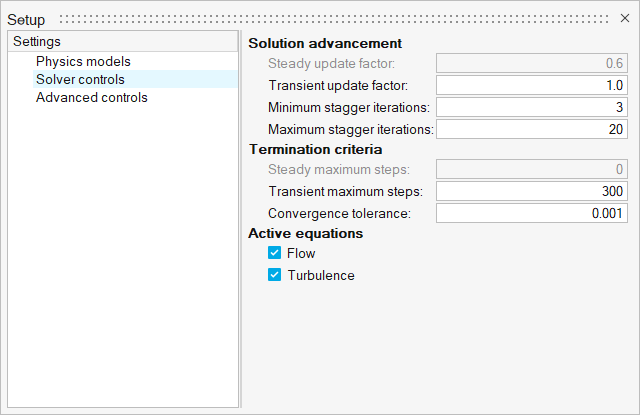
Set Up the Simulation Parameters and Solver Settings

  1. From the Flow ribbon, click the Physics tool.


    Figure 5.
    The Setup dialog opens.
  2. Under the Physics models setting:
    1. Verify that the Incompressible option is selected under Single phase flow.
    2. Set the Time marching to Transient.
    3. Set the Time step size to 0.01 and the Final time to 0.0.
    4. Select Spalart-Allmaras as the Turbulence model.


    Figure 6.
  3. Click the Solver controls setting.
    1. Set the Minimum stagger iterations to 3.
    2. Set the Maximum stagger iterations to 20.
    3. Set the Transient maximum steps to 300.


    Figure 7.
  4. Close the dialog and save the model

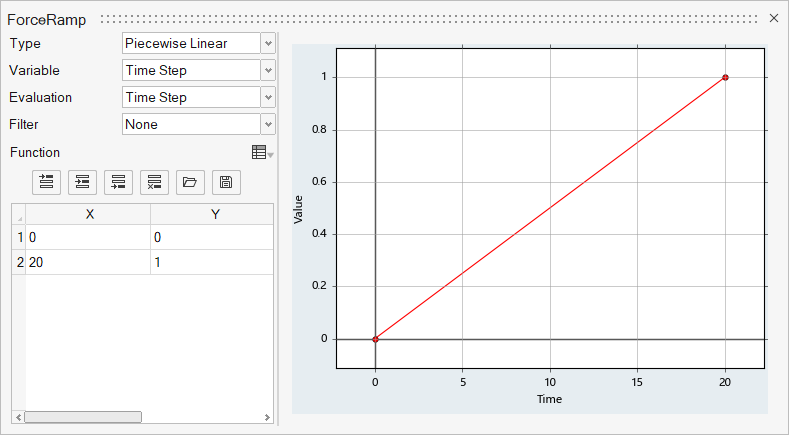
Create a Multiplier Function

The force acting on the beam, due to the flow, will be ramped gradually over the first few time steps. After these first few time steps, the complete force from the fluid will be transferred to the beam without any ramping. This will be achieved using a Multiplier Function. In the next few steps you will create a linear multiplier function which will later be assigned as a force multiplier function for load acting on the beam.

  1. From the Flow ribbon, click the arrow next to the Setup tool set, then select Multipliers.


    Figure 8.
    The Multiplier Library opens.
  2. Click to add a new multiplier.
  3. In the multiplier creation dialog, change the name of the multiplier function to ForceRamp by clicking on the top-left corner.
  4. Set the Type to Piecewise Linear and the Variable to Time Step.
  5. Verify that the Evaluation is set to Time Step.
  6. Enter the table values according to the figure below.


    Figure 9.

Assign Material Properties

  1. From the Flow ribbon, click the Material tool.


    Figure 10.
  2. Select the model body.
    The entire solid is highlighted.
  3. Select Water from the drop-down in the microdialog.


    Figure 11.
  4. On the guide bar, click to execute the command and exit the tool.

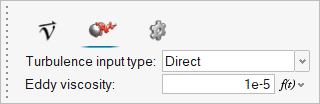
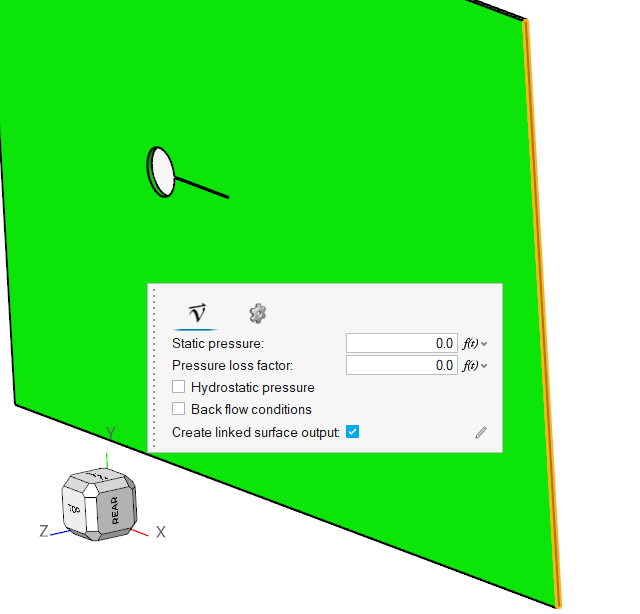
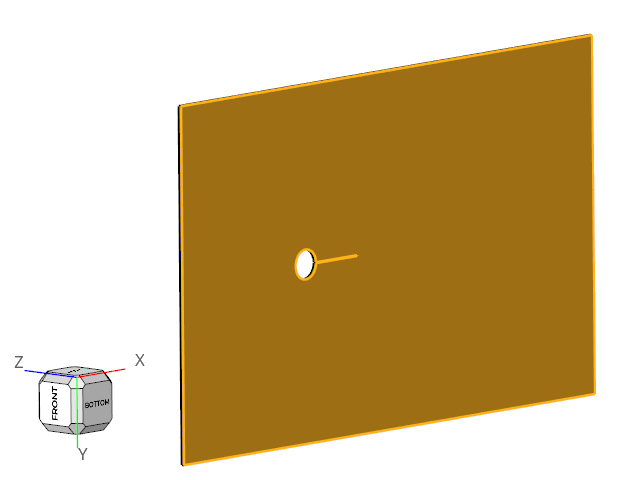
Assign the Flow Boundary Conditions

  1. From the Flow ribbon, click the Constant tool.


    Figure 12.
  2. Select the left-most face on the negative x-axis, as shown in the figure below.
  3. In the microdialog, choose Cartesian for the inflow velocity type and set X velocity to 10 m/s.


    Figure 13.
  4. Click the Turbulence tab in the microdialog. Choose Direct for the Turbulence input type and set Eddy viscosity to 1e-5 m2/sec.


    Figure 14.
  5. Click on the guide bar.
  6. Click the Outlet tool.


    Figure 15.
  7. Select the right-most face on the positive x-axis, as shown in the figure below
  8. In the microdialog, verify that both the static pressure and the pressure loss factor are set to 0.


    Figure 16.
  9. Click on the guide bar.
  10. Click the Slip tool.


    Figure 17.
  11. Select the right-most face on the negative z-axis, as shown in the figure below.


    Figure 18.
  12. On the guide bar, click to execute the command and remain in the tool.
  13. In the Boundaries legend, double-click Slip, rename it to z_neg, and press Enter.
  14. Rotate the model and select the opposite face.
  15. Click on the guide bar.
  16. In the Boundaries legend, rename Slip to z_pos.
  17. Select the right-most face on the positive y-axis, as shown in the figure below.


    Figure 19.
  18. Click on the guide bar.
  19. In the Boundaries legend, rename Slip to y_pos.
  20. Rotate the model and select the opposite face.
  21. Click on the guide bar.
  22. In the Boundaries legend, rename Slip to y_neg.
  23. In the Boundaries legend, right-click Default Walls and select Isolate.
  24. Click the No Slip tool.


    Figure 20.
  25. Select the cylinder face, as shown in the figure below.


    Figure 21.
  26. Click on the guide bar.
  27. In the Boundaries legend, rename Wall to cylinder.
  28. Right-click cylinder and select Hide.

Set Up Motion

Define the Mesh Motion Type

In the introduction it was discussed that the structural solver is responsible for calculating the displacement and passes on the calculated displacements to AcuSolve. In the following steps, you will set up the connection between AcuSolve and the external code, which in this case is OptiStruct.
  1. From the Motion ribbon, click the Settings tool.


    Figure 22.
    The Setup dialog opens.
  2. Change the Mesh motion to Arbitrary.
  3. Click the Solver controls setting and activate Mesh deformation.
  4. Click the External code setting and activate the External code option.
  5. Set the External Solver to OptiStruct and the Communication type to Socket.
  6. Deactivate the External socket option and set the Socket host to localhost.
  7. Set the Socket port to 48002.
    The socket port depends on the structural solver. 48002 is the OptiStruct default and is thus used for this example. Refer to the manual of the structural solver you are using to determine the correct port number to be entered here.
  8. Activate Scale fields and select ForceRamp for Multiplier function.
    This will gradually ramp up the forces transmitted from the external code over the first few steps as specified by the multiplier function (20 time steps in this case).


    Figure 23.
  9. Close the dialog and save the model.

Define the Mesh Displacement Boundary Conditions

  1. From the Motion ribbon, click the External Surface tool.


    Figure 24.
  2. Select the beam faces, as shown in the figure below.
  3. In the microdialog, select Factor for the Gap method and set Gap factor to 0.


    Figure 25.
  4. In the External Code Surface legend, rename the External surface to beam.
  5. Click on the guide bar.
  6. Click the No Constraints tool.


    Figure 26.
  7. Select the external surfaces of beam.
  8. Click on the guide bar.
  9. Press A to show all surfaces.
  10. Click the Planar Slip tool.


    Figure 27.
  11. Select the right-most face on the negative z-axis, as shown in the figure below


    Figure 28.
  12. Click on the guide bar.
  13. In the Mesh Motion legend, rename Planar Slip to z_neg.
  14. Rotate the model and select the opposite face.
  15. In the Mesh Motion legend, rename Planar Slip to z_pos.
  16. Click on the guide bar.
  17. Turn on the display of all surfaces and save the model.

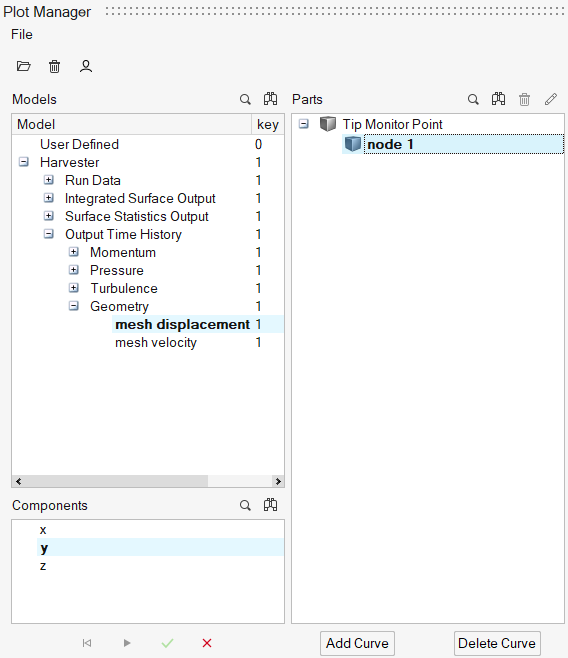
Define Time History Output Points

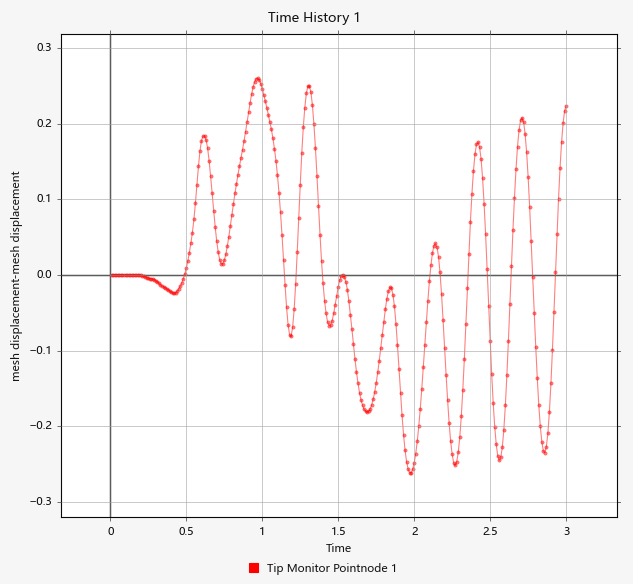
Time History Output commands enable you to extract the nodal solution at any point within the domain. In this simulation, it would be interesting to observe the displacement at the tip of the cantilever beam.

  1. Form the Solution ribbon, click the body of the Probe tool.


    Figure 29.
  2. Select the top point of the beam tip end on the right-most face of the negative z-axis, as shown in the figure below.
  3. In the microdialog, set the Point Radius to 0.01.


    Figure 30.
  4. In the Point Probes legend, rename Point Probe to Tip_Monitor_Point.
  5. Click on the guide bar.

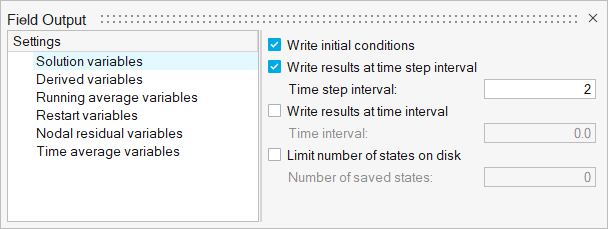
Define Nodal Outputs

The nodal output command specifies the nodal output parameters; for instance, output frequency, number of saved states, and so on.

  1. From the Solution ribbon, click the Field tool.


    Figure 31.
    The Field Output dialog opens.
  2. Under solution variables:
    1. Activate Write initial conditions.
    2. Activate Write results at time step interval.
    3. Set the Time step interval to 2.


    Figure 32.
  3. Close the dialog and save the model.

Run OptiStruct

  1. Start OptiStruct from the Windows Start menu by clicking Start > Altair <version> > Compute Console.
  2. Click next to Input file(s).
  3. Browse to the directory where you saved the OptiStruct model file.
  4. Select the slab_dcfsi.fem file.
  5. Activate Use solver control.


    Figure 33.
  6. Click Run to launch OptiStruct.

Run AcuSolve

  1. From the Solution ribbon, click the Run tool.


    Figure 34.
  2. Set the Parallel processing option to Intel MPI.
  3. Optional: Set the number of processors to 4 or 8 based on availability.
  4. Deactivate the Automatically define pressure reference option.
  5. Expand Default initial conditions and deactivate Pre-compute flow.
  6. Set the x velocity to 10 m/s.
  7. Set the eddy viscosity to 1e-05 m2/sec.
  8. Leave the remaining options as default and click Run to launch AcuSolve.


    Figure 35.
  9. Right-click the solver job in the Run Status dialog and select View log file.
    As the solution progresses, progress is reported in this window.

    When AcuSolve is started, it will listen to the socket port specified while setting up the external code coupling for an initial communication from OptiStruct. You must make sure to start the OptiStruct run which will initialize the socket port for communication. Once the connection is established, the solvers will alternatively send and receive data through the simulation steps.

Plot Time History

  1. Right-click the solver job in the Run Status dialog and select Plot time history.
  2. In the Plot Manager dialog, click to create a new plot.
  3. Expand Output Time History > Geometry then select mesh displacement.
  4. Set Components to y.
  5. In the Parts field, choose node 1 under Tip Monitor Point to displace the time history of the beam end.
    Figure 36.


    Figure 37. Mesh_y_displacement plot at beam tip

    The plot above shows the displacement of the tip of the beam due to the fluid forces as the beam interacts with the flow.

Post-Process the Results with HM-CFD Post

In this step, you will create an animation of pressure.
  1. Once the solution is completed, navigate to the Post ribbon.
  2. From the menu bar, click File > Open > Results.
  3. Select the AcuSolve .log file in your problem directory to load the results for post-processing.
    The solid and all the surfaces are loaded in the Post Browser.

    You can also import the results into HyperMesh CFD Post by right-clicking a solver job in the Run Status dialog and selecting Visualize results.

  4. Click the Bottom face on the View Cube to align the model.


    Figure 38.
  5. Right-click the z_pos boundary in the Post Browser and select Isolate.
  6. Move the slide bar at the bottom of the modeling window to 74/151.


    Figure 39.
  7. Right-click z_pos again and select Edit.
  8. In the display properties microdialog, set the display to pressure.
  9. Activate the Legend toggle and set the upper and lower bounds to -65000 Pa and 55000 Pa, respectively.
  10. Click and set the Colormap Name to Rainbow Uniform.


    Figure 40.
  11. Click on the guide bar.
  12. Click on the Animation toolbar to view a live animation of the flow.


    Figure 41.
  13. Save the animation.
    1. Go to File > Screen Capture > Advanced Screen Capture.
    2. Click and uncheck Include mouse cursor.
    3. Set the frame rate to 24 and select GIF as the video setting.
    4. Click on the toolbar then drag over the area you want to record.
    5. Click to begin recording and the same icon to stop recording.
    6. Name the file and save it.

Summary

In this AcuSolve tutorial, you successfully set up and solved an FSI problem using the Direct Coupling, or DC-FSI approach. DC-FSI approach is a co-simulation approach where both the structural and the fluid solvers run simultaneously, and exchange information at each time step of the simulation. The fluid solver passes the flow and pressure information to the structural solver, which are used to determine the displacements in the structure. The structural solver then passes the displacement information to the fluid solver, which then recalculates the flow and pressure field. Both the solvers thus update and exchange the results of the simulation to achieve the solution. You started the tutorial by creating a database in HyperMesh CFD and setting up the basic simulation parameters. Then, you defined the parameters for setting up the connection between AcuSolve and the structural solver, and generated a solution with co-simulation. Results were post-processed in HyperMesh CFD, where you generated an animation of the beam’s displacement as it interacted with the fluid flow.