OS-E: 3000 Cross-section Optimization of a Spot Welded Tube

A tube made of two sheet metal pieces is intended to carry a load in both bending and torsion. The cross-section of the tube may be of any shape, but due to manufacturing requirements, it must remain constant through the entire length.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

Model Description

Conventional shape optimization can be used to optimize the cross-section, but setting up the variables is time consuming. With topography optimization and pattern grouping, cross-section shape optimization can be performed in a fraction of the set up time. All optimization set up is done using the Optimization panel and its subpanels in HyperMesh.

The loads and constraints are applied to the flanges at the ends of the tube, and are shown in Figure 1. Spot welds connect the two pieces of the tube along the flanges at regular intervals.

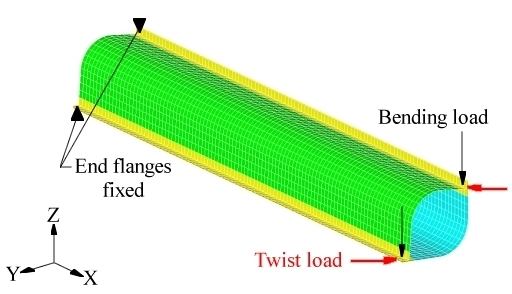
fig1p1
Figure 1. Loads and Constraints for the Spot Welded Tube
The initial cross-section of the tube is arbitrarily chosen to be roughly circular. Two similar topography variables are defined to allow the shape of the tube to change. The two variables assign the blue and green pieces to be in the design domain while the flanges remain in their original shape. The topography variables are in the Bulk Data section using the DTPG card as.
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
DTPG 1 PSHELL 1            
+ 2.5 85.0 NO 5.0 NORM     NONE  
+ PATRN 1 0.0 0.0 0.0 1.0 0.0 0.0  

The draw height of 5.0, combined with the upper and lower bounds of 2.0 and -2.0, allow a bead height of 10.0 model units in both directions (inward and outward) and a bead growth direction normal to the surface of the tube. A linear type pattern grouping is applied for this problem. This means that the beads formed during the topology optimization will be constant along a line parallel to the direction defined -- the central axis (X-axis) of the tube, in this case. By setting this pattern grouping option, the cross-section of the tube will be allowed to change, but will remain constant through the length of the tube.

The objective was set to minimize the weighted compliance of both load cases. In this case, both load cases were weighted equally. The mass of the tube was constrained to be below the initial value. OptiStruct generated the following solution for the model (Figure 2).

spotweldexample
Figure 2. Optimized Cross-Section for the Tube
The solution is not completely smooth, but the basic shape of the tube is clear. The lower half of the tube has been lowered to increase the bending stiffness of the section while the upper half of the tube runs directly from one flange to the other to support the shear force generated by the twist load (Figure 3).

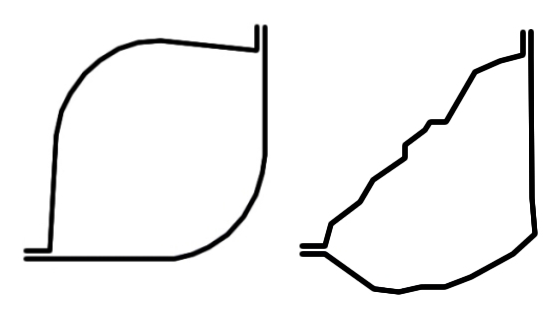
fig1p3
Figure 3. Cross-Sections of the Tube Before and After Optimization

Results

To verify the OptiStruct solution, a smooth model of the tube is built based upon the results. This model is shown in Figure 4 and Figure 5. Static analysis shows the optimized cross-section after smoothing to have a 35% lower peak deflection for torsion and an 18% lower peak deflection for bending. Additionally, the mass of the part was reduced by 2.2%.

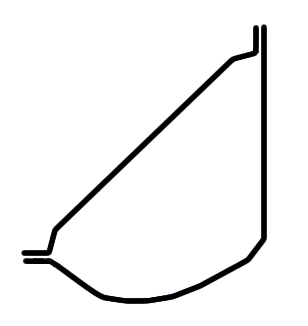
fig1p4
Figure 4. Smoothed Cross-Section of the Tube

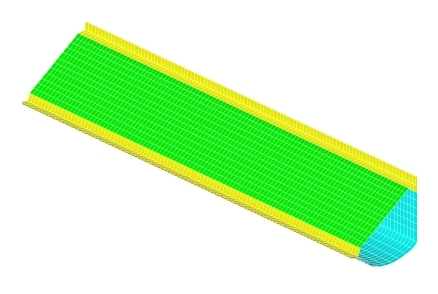
fig1p5
Figure 5. Finite Element Model of the Smoothed Optimized Tube