OS-V: 0291 Hertzian Contact - Elastic Sphere and Rigid Half-space
Hertzian contact is demonstrated using OptiStruct for an elastic sphere and rigid half-space problem.

Figure 1. Model
Model Files
Benchmark Model
- Material Properties
- Value
- Young's modulus (E)
- 210000
- Poisson's ratio ( )
- 0.3
- R
- 30
- d
- 0.1 (enforced z-displacement)
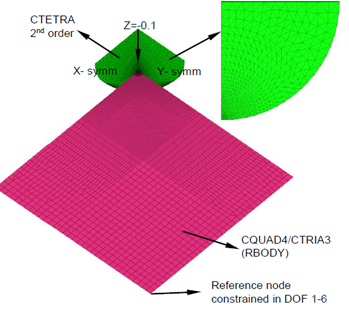
Figure 2. Model Details
Analytical Results:
The analytical solutions are provided by Popov, 2010. The derivation of the analytical solution is beyond the technical scope of this document. Some key variables of the analytical solution are as follows:
- Radius of the sphere.
- Depth of indentation.
- Young's modulus.
- Poisson's ratio.
Results
| Pressure/Stress (Magnitude) | r/a | |
|---|---|---|
| Analytical Result | OptiStruct (S2S)-Contact Pressure | |
| 8482 | 8525 | 0 |
| 8350 | 8300 | 0.2 |
| 7700 | 7675 | 0.4 |
| 6800 | 6990 | 0.6 |
| 5100 | 5200 | 0.8 |
| 0 | 1345 | 1 |
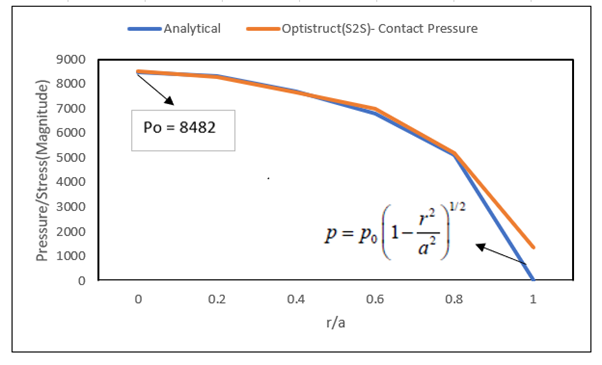
Figure 3. Analytical Results versus OptiStruct Results

Figure 4. Contact Traction/Normal (Pressure)

Figure 5. Stresses 2D and 3D - Z Stress

Figure 6. SPC Forces