Loads and Boundary Conditions
The following boundary conditions are outlined here.
Static Loads and Boundary Conditions
- Loads applied directly to grid points
- Pressure on surfaces
- Gravity loads
- Centrifugal forces due to steady rotation
- Equivalent loads resulting from:
- thermal expansion
- enforced deformations of structural elements
- enforced displacements of grid points
Any number of load sets can be defined in the Bulk Data section of the input file. However, only those sets selected in the Subcase Information section (as described in Linear Static Analysis, Inertia Relief and Nonlinear Static Analysis) will be used in the problem solution. The manner in which each type of load is selected is specified on the associated Bulk Data statement description.
The FORCE statement is used to define a static load applied to a grid point in terms of components defined by a local coordinate system. The orientation of the load components depends on the type of local coordinate system used to define the load.
The FORCE1 statement is used if the direction is determined by a vector connecting two grid points.
The MOMENT and MOMENT1 statements are used to define the application of a concentrated moment at a grid point.
The ACCEL, ACCEL1, and ACCEL2 entries are used to define the application of static acceleration loads at grid points in the model.
Pressure loads on triangular and quadrilateral elements are defined with a PLOAD2 card. The positive direction of the loading is determined by the order of the grid points on the element connection card (using the right-hand rule). The magnitude and direction of the load is automatically computed from the value of the pressure and the coordinates of the connected grid points. The load is applied to the connected grid points.
PLOAD pressure loads are used in a similar fashion to define the loading of any three or four grid points, regardless of whether or not they are connected with two-dimensional elements.
Pressure loads on the HEXA, PENTA and TETRA solid elements are defined with the PLOAD4 card. The pressure is defined positively outward from the element. The magnitude and direction of the equivalent grid point forces are automatically computed using the iso-parametric shape functions of the element to which the load has been applied. Pressure loads on the QUAD4 and TRIA3 elements can also be applied using the PLOAD4 card.
The PLOAD1 card is used to describe concentrated, uniformly distributed or linearly distributed loads on the CBAR or CBEAM elements.
The GRAV Bulk Data Entry is used to specify a gravity load by providing the components of the gravity vector in any defined coordinate system. The gravity load is obtained from the gravity vector and the mass matrix of the structural model. Because the gravitational acceleration is not calculated at scalar points, you are required to introduce gravity loads at scalar points directly.
The RFORCE statement is used to define a static loading condition due to a centrifugal force field. A centrifugal force load is specified by the designation of a grid point that lies on the axis of rotation and by the components of rotational velocity and acceleration in any defined coordinate system. In the calculation of the centrifugal force, the mass matrix pertains to a set of distinct rigid bodies connected to grid points. Deviations from this viewpoint, such as the use of scalar points or the use of mass coupling between grid points, can result in errors.
Temperature loads can only be defined at grid points. The temperatures of the connected grid points are given on the TEMP and TEMPD Bulk Data Entries. The thermal expansion coefficients are defined on the material definition cards. The mere presence of a thermal field does not imply the application of a thermal load. A thermal load will not be applied unless you make a specific request in the Subcase Information section.
The LOAD Bulk Data card defines a static loading condition that is a linear combination of load sets consisting of loads applied directly to grid points, pressure loads, gravity loads, and centrifugal forces. This card must be used if gravity loads are to be used in combination with loads applied directly to grid points, pressure loads, or centrifugal forces. The application of the combined loading condition is requested in the Subcase Information section by selecting the set number of the LOAD combination.
It should be noted that the equivalent loads (thermal and enforced displacement) must have unique set identification numbers and be selected separately in the Subcase Information section. For any particular solution, the total load will be the sum of the applied loads (grid point loading, pressure loading, gravity loading, and centrifugal forces) and the equivalent loads.
Zero enforced displacements may be specified on SPC or SPC1 cards. Zero displacements result in non-zero forces on the grid point constrained (SPC forces).
The SPCADD statement allows the combination of different SPC sets.
For inertia relief, the reaction degrees of freedom for the computation of the acceleration load are defined through SUPORT or SUPORT1 statements. Up to six degrees of freedom can be defined per subcase.
Non-zero enforced displacements may be specified on SPC or SPCD cards. The SPC card specifies both the component to be constrained and the magnitude of the enforced displacement. The SPCD card only specifies the magnitude of the enforced displacement. When an SPCD card is used, the component to be constrained must be specified on either an SPC or an SPC1 card. The use of the SPCD card avoids the decomposition of the stiffness matrix when changes are only made in the magnitudes of the enforced displacements.
The equivalent loads resulting from enforced displacements of grid points are calculated by the program and added to the other applied loads.
If the magnitudes of the enforced displacements are specified on SPC cards, the application of the load is automatic when you select the associated SPC set in the Subcase Information section.
If the magnitude of the displacement is defined on an SPCD card, the load is applied if you select the associated LOAD set in the Subcase Information section.
Inertia Relief
Allows the simulation of unconstrained structures. Typical applications are an airplane in flight, suspension parts of a car, or a satellite in space.
With inertia relief, the applied loads are balanced by a set of translational and rotational accelerations. These accelerations provide body forces, distributed over the structure in such a way that the sum total of the applied forces on the structure is zero. This provides the steady-state stress and deformed shape in the structure as if it were freely accelerating due to the applied loads. Boundary conditions are applied only to restrain rigid body motion. Because the external loads are balanced by the accelerations, the reaction forces corresponding to these boundary conditions are zero.
This calculation is automated.
Inertia relief boundary conditions may be defined in the Bulk Data section of the input deck or they may be determined automatically by the solver.
Use SUPORT Entries
- PARAM,INREL,-1 is used to activate inertia relief.
- The SUPORT and SUPORT1 Bulk Data Entries are used to define up to six reaction degrees of freedom of the free body.
- SUPORT entries will be used in all relevant subcases and therefore do not need to be referenced in the Subcase Information section.
- SUPORT1 entries need to be referenced by a SUPORT1 data selector statement for use within a subcase.
Automatic Support Generation
- Inertia relief boundary conditions may be generated automatically by using PARAM,INREL,-2.
- Inertia relief boundary conditions may be generated automatically by using PARAM,INREL,-2.
- The METHOD parameter on PARAM,INREL can reference the ID of EIGRL or EIGRA entry.
- Eigenvalue subcases are internally generated to calculate the rigid body modes, inertial loads, and support points.
In OptiStruct, inertia relief can be applied to linear static, nonlinear static analyses, and modal frequency response analyses. For nonlinear static analysis with contact, by default, only freeze contact is supported with inertia relief. If non-freeze contact is present, PARAM,IR4NLCON,YES can be used to allow the model to run with inertia relief. A static subcase with inertia relief is not supported by default in a linear buckling analysis. PARAM,INRELBCK,1 or PARAM,INRELBCK,2 can be used to attempt Buckling Analysis based on Inertia relief. Inertia relief is meaningless in normal modes analysis.
PARAM,PRINFACC,1 can be used to print additional information such as the output of inertial relief rigid body forces and accelerations in the .out file.
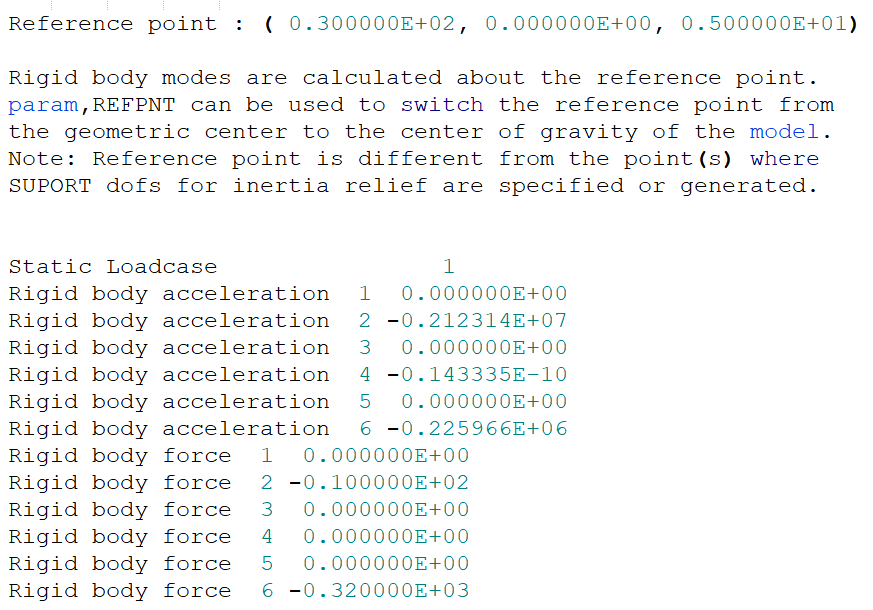
Figure 1.
Theory
For static analysis of structures with rigid body modes, inertia relief calculations can be included in the solution process. In particular, structures with non-structural masses may be significantly influenced by inertia relief effects. PARAM,INREL,-1 or PARAM,INREL,-2 can be used to allow the inclusion of inertia relief calculations.
- Load vector
- Global mass matrix
- The set of all the rigid body modes that satisfy the boundary conditions on the model
- Reduced displacement vector
- Reduced mass matrix
- Reduced load vector
- PARAM,INREL,-1 or a
Constrained Structure using
PARAM,INREL,-2:If PARAM,INREL,-1 is set or for PARAM,INREL,-2, if the structure is constrained in any way, the static analysis solution under inertia relief uses:
(3) Where, is calculated using the original stiffness matrix (), plus constraints at the SUPORT degrees of freedom to render the displacements at the SUPORTs to be zero. SUPORT degrees of freedom are specified by you (for PARAM,INREL,-1) or automatically generated by OptiStruct (for PARAM,INREL,-2).
- PARAM,INREL,-2 for a Free-Free
Structure:When PARAM,INREL,-2 is used for a Free-Free structure, an alternative method is used by default. In this method, OptiStruct imposes MPCs instead of automatically generating SUPORT degrees of freedom. This modifies the equation as:
(4) Equation 4 is a combination of and and the additional requirement that the inertia-relieved displacement be orthogonal to the rigid body modes (). Subsequently, this MPC augmentation has been further modified as (ignores equation ):(5)
Frequency Response Loads and Boundary Conditions
Frequency dependent dynamic loads are applied at grid points. There are two different definitions available.
Any number of load sets can be defined in the Bulk Data section of the input file. However, only those sets selected in the Subcase Information section (as described in Frequency Response Analysis) will be used in the problem solution. The manner in which each type of load is selected is specified on the associated Bulk Data statement description.
For both definitions, a combination of DAREA, FORCE, FORCE1, FORCE2, MOMENT, MOMENT1, MOMENT2, PLOAD, PLOAD1, PLOAD2, PLOAD4, and RLOAD, or SPCD define the amplitude of an excitation force or motion, respectively. A DPHASE reference defines the phase angle , and a DELAY reference defines the delay . The quantities , , , and , are frequency dependent. They are defined using TABLED1, TABLED2, TABLED3, or TABLED4.
It is recommended that SPCD be used for enforced motion. If the old inferior Large Mass Method is used for modal frequency response analysis with EIGRA, use PARAM,AMSESLM for better accuracy.
The range for the loading frequency is defined using the FREQ, FREQ1, FREQ2, FREQ3, FREQ4, or FREQ5 Bulk Data statements.
The DLOAD Bulk Data card defines a static loading condition that is a linear combination of load sets consisting of loads applied directly to grid points. The application of the combined loading condition is requested in the Subcase Information section by selecting the set number of the DLOAD combination.
Zero enforced displacements may be specified on SPC or SPC1 cards.
The SPCADD statement allows the combination of different SPC sets.
Combinations of dynamic loads (DAREA) with static loads (FORCE, FORCE1, FORCE2, MOMENT, MOMENT1, MOMENT2, PLOAD, PLOAD1, PLOAD2, PLOAD4, and RLOAD), is supported.
Transient Response Loads and Boundary Conditions
Transient dynamic loads are applied at grid points. Two different definitions are available.
Any number of load sets can be defined in the Bulk Data section of the input file. However, only those sets selected in the Subcase Information section (as described in Transient Response Analysis) will be used in the problem solution. The manner in which each type of load is selected is specified on the associated Bulk Data statement description.
The TLOAD1 and TLOAD2 Bulk Data Entries define time dependent loads.
For both definitions, applied loads (DAREA, FORCEx, PLOADx, etc.), enforced motion (SPC/SPCD) or temperature (TEMP/TEMPD) define the amplitude . A DELAY statement defines the delay.
The DLOAD Bulk Data Entry defines a static loading condition that is a linear combination of load sets consisting of loads applied directly to grid points. The application of the combined loading condition is requested in the Subcase Information section by selecting the set number of the DLOAD combination.
Transient initial conditions are defined using a TIC Bulk Data Entry. Initial displacements and initial velocities can be defined.
Zero enforced displacements may be specified on SPC or SPC1 cards.
The SPCADD statement allows the combination of different SPC sets.
Combinations of dynamic loads with static loads are not currently supported.
It is recommended that SPCD be used for enforced motion. If the old inferior Large Mass Method is used for modal transient analysis with EIGRA, use PARAM, AMSESLM, for better accuracy.