/BEM/DAA

Block Format Keyword Doubly Asymptotic Approximation for Underwater Explosion, where the fluid mass matrix is computed by boundary element method.

Format

(1)	(2)	(3)	(5)	(6)	(7)	(8)	(9)
/BEM/DAA/`daa_ID`/`unit_ID`
`daa_title`
`surf_ID`	`grav_ID`
$ρ$ $ρ$		`C`	`P`_min
`X`_s		`Y`_s	`Z`_s
`I`_form	`Ipri`	`Ipres`		`Kform`	`Freesurf`	`Afterflow`	`Integr`

Insert if Ipres=1

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`P`_m		$θ$ $θ$		`a`		$a_{θ}$ $a_{θ}$

Insert if Ipres=2

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fct_ID`_P		`Fscale`_P

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`X`_c		`Y`_c		`Z`_c

Insert if grav_ID > 0 or Freesurf=2

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`X`_A		`Y`_A		`Z`_A
`Dir-X`		`Dir-Y`		`Dir-Z`

Definition

Field	Contents	SI Unit Example
`daa_ID`	DAA block identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`daa_title`	DAA block title. (Character, maximum 100 characters)
`surf_ID`	Wet surface identifier. 2 3 (Integer)
`grav_ID`	/GRAV option identifier. (Integer)
$ρ$ $ρ$	Fluid density. (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`C`	Fluid sound speed. (Real)	$[\frac{m}{s}]$ $[\frac{m}{s}]$
`P`_min	Pressure cutoff (< 0). Default = -10³⁰ (Real)	$[Pa]$ $[Pa]$
`X`_s	X-coordinate of standoff point. 3 (Real)	$[m]$ $[m]$
`Y`_s	Y-coordinate of standoff point. 3 (Real)	$[m]$ $[m]$
`Z`_s	Z-coordinate of standoff point. 3 (Real)	$[m]$ $[m]$
`Iform`	BEM solution flag. =1 (Default) Gauss Integration. = 2 Analytical integration. (Integer)
`Ipri`	Printout flag level. =1 (Default) Reduced printout. = 2 Full printout. (Integer)
`Ipres`	Pressure loading flag. 6 =1 Pressure computed as $P_{i} (t) = P_{m} e^{- \frac{t}{θ}}$ $P_{i} (t) = P_{m} e^{- \frac{t}{θ}}$ . = 2 Input by function. (Integer)
`Kform`	Analysis flag. =1 (Default) DAA1 formulation = 2 High frequency (Integer)
`Freesurf`	Free surface flag. 6 =1 (Default) No = 2 Yes (Integer)
`Afterflow`	Afterflow computation. 7 =1 No = 2 (Default) Yes (Integer)
`Integr`	Time integer flag. =1 First order = 2 (Default) Second order (Integer)
`P`_m	Maximum pressure. 5 (Real)	$[Pa]$ $[Pa]$
$θ$ $θ$	Decay time. (Real)	$[s]$ $[s]$
`a`	Maximum pressure constant. 5 (Real)
$a_{θ}$ $a_{θ}$	Pressure decay time constant. 5 (Real)
`fct_ID`_P	Incident pressure function identifier. (Integer)
`Fscale`_P	Ordinate (pressure) scale factor for `fct_ID`_P. (Real)	$[Pa]$ $[Pa]$
`X`_C	X-coordinate of explosive charge. (Real)	$[m]$ $[m]$
`Y`_C	Y-coordinate of explosive charge. (Real)	$[m]$ $[m]$
`Z`_C	Z-coordinate of explosive charge. (Real)	$[m]$ $[m]$
`X`_A	X-coordinate of point A on the free surface. (Real)	$[m]$ $[m]$
`Y`_A	Y-coordinate of point A on the free surface. (Real)	$[m]$ $[m]$
`Z`_A	Z-coordinate of point A on the free surface. (Real)	$[m]$ $[m]$
`Dir-X`	X-component of the normal to the free surface plane. (Real)
`Dir-Y`	Y-component of the normal to the free surface plane. (Real)
`Dir-Z`	Z-component of the normal to the free surface plane. (Real)

Comments

The entire structure must be modeled. Symmetric analysis is not supported.
The surface normal $n$ $n$ should be pointed into the fluid.
Standoff point defined with (X_s, Y_s, Zs) is the location where the incident pressure wave is given at time t=0:

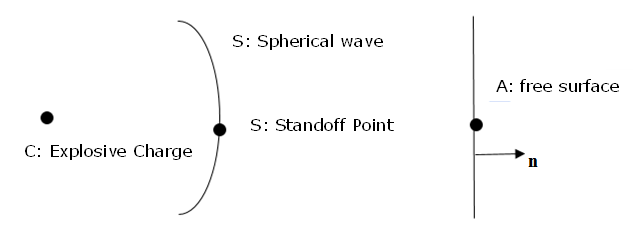
Figure 1.
A plane wave can be simulated using a spherical wave and putting the explosive charge far enough away.

Pressure at the standoff point as a function of time is:(1)

P_{i} (t) = P_{m} e^{- \frac{t}{θ}}

$P_{i} (t) = P_{m} e^{- \frac{t}{θ}}$

Where,

$P_{m}$ $P_{m}$: Maximum pressure
$t$ $t$: Time
$θ$ $θ$: Decay time

The maximum pressure and decay time can be calculated using:(2)

P_{m} = K {[\frac{W^{\frac{1}{3}}}{R}]}^{a}

$P_{m} = K {[\frac{W^{\frac{1}{3}}}{R}]}^{a}$

(3)

θ = K_{θ} W^{\frac{1}{3}} {[\frac{W^{\frac{1}{3}}}{R}]}^{a_{θ}}

$θ = K_{θ} W^{\frac{1}{3}} {[\frac{W^{\frac{1}{3}}}{R}]}^{a_{θ}}$

$W$ $W$: Explosive mass.
$R$ $R$: Distance to the explosion.
$K$ $K$ , $α$ $α$ , $K_{θ}$ $K_{θ}$ and $a_{θ}$ $a_{θ}$: Constants depending on the explosive.

W

$W$ in kg,

R

$R$ in meter,

P_{m}

$P_{m}$ in MPa and in ms.

	$K$ $K$	$α$ $α$	$K_{θ}$ $K_{θ}$	$a_{θ}$ $a_{θ}$
TNT	52.12	1.180	0.0895	-0.185
PETN	56.21	1.194	0.0860	-0.257
HBX	53.51	1.144	0.0920	-0.247

A free surface is a plane defined by a point and its normal vector.
The afterflow normal velocity is calculated as:(4)
$v_{a f t e r f l o w} = \frac{\cos γ}{ρ R} \int_{0}^{t} P (t) d t$ $v_{a f t e r f l o w} = \frac{\cos γ}{ρ R} \int_{0}^{t} P (t) d t$

P

Fluid point.

C

Explosive charge point.

S

Standoff point.

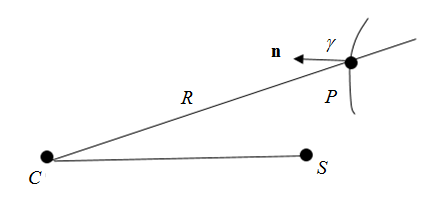
Figure 2.

Littlewood, J. de Runtz T. 2004. "USA Code". Mecalog Workshop, Sophia Antipolis, France, 2004

Cole, Robert H. Underwater Explosion. Princeton University Press, 1948