/FAIL/HOFFMAN

Block Format Keyword Hoffman failure criterion for modeling the failure of composite materials. This criterion is available for solids and shells.

Format

(1)	(3)	(5)	(7)	(9)	(10)
/FAIL/HOFFMAN/`mat_ID`/`unit_ID`
$σ_{1}^{t}$	$σ_{2}^{t}$	$σ_{1}^{c}$	$σ_{2}^{c}$	${\bar{σ}}_{12}$
$τ_{\max}$	`F`_cut			`I`_{fail_sh}	`I`_{fail_so}

Optional Line:

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fail_ID`

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	(Optional) Unit identifier. (Integer, maximum 10 digits)
$σ_{1}^{t}$	Longitudinal tensile strength. Default = 10²⁰ (Real)	$[Pa]$
$σ_{2}^{t}$	Transverse tensile strength. Default = 10²⁰ (Real)	$[Pa]$
$σ_{1}^{c}$	Longitudinal compressive strength. Default = 10²⁰ (Real)	$[Pa]$
$σ_{2}^{c}$	Transverse compressive strength. Default = 10²⁰ (Real)	$[Pa]$
${\bar{σ}}_{12}$	Shear strength. Default = 10²⁰ (Real)	$[Pa]$
$τ_{\max}$	Dynamic time relaxation. 5 Default = 10²⁰ (Real)	$[s]$
`F`_cut	Shell tensor filtering frequency. Default = 0.0 (Real)	$[\frac{1}{s}]$
`I`_{fail_sh}	Shell failure model flag. = 0 (Default) Shell is never deleted and no stress softening. = 1 Shell is deleted, if damage is reached for one layer. = 2 Shell is deleted, if damage is reached for all shell layers. (Integer)
`I`_{fail_so}	Solid failure model flag. = 0 Solid is never deleted and no stress softening. = 1 (Default) Solid is deleted, if damage is reached for one integration point of solid. = 2 Solid is deleted, if damage is reached for all integration points. (Integer)
`fail_ID`	(Optional) Failure criteria identifier. 4 (Integer, maximum 10 digits)

Example

/UNIT/1
                  kg                  mm                  ms
/FAIL/HOFFMAN/1/1
#           SIGMA_1T            SIGMA_2T            SIGMA_1C            SIGMA_2C            SIGMA_12
                 0.6                0.525                 0.8                0.75                0.075  
#           TAU_MAX                 FCUT                                 IFAIL_SH            IFAIL_SO
           0.005932                                                              2                    2

Comments

This failure model is available for shells and solids. It considers a composite material ply with the fibers oriented in the direction 1 (also denoted m1) and the matrix oriented in transverse direction, that is, in direction 2 (and 3 for solids). Each direction considers a critical strength value in tension and compression as;
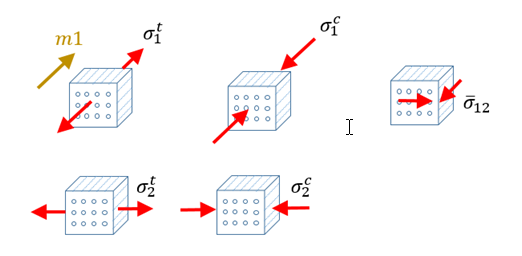Figure 1.

Where, $σ_{1}^{t}$ , $σ_{2}^{t}$ , $σ_{1}^{c}$ , $σ_{2}^{c}$ , ${\bar{σ}}_{12}$ are respectively the critical strength in tension for direction 1, in tension for direction 2, in compression for direction 1, in compression for direction 2 and in shear.
The failure criterion for shells is written as:(1)
$F = (\frac{1}{σ_{1}^{t}} - \frac{1}{σ_{1}^{c}}) σ_{1} + (\frac{1}{σ_{2}^{t}} - \frac{1}{σ_{2}^{c}}) σ_{2} + \frac{σ_{1}^{2}}{σ_{1}^{t} \cdot σ_{1}^{c}} + \frac{σ_{2}^{2}}{σ_{2}^{t} \cdot σ_{2}^{c}} - \frac{σ_{1} \cdot σ_{2}}{σ_{1}^{t} \cdot σ_{1}^{c}} + \frac{σ_{12}^{2}}{{\bar{σ}}_{12}^{2}} \leq 1$

For solids the criterion becomes:(2)
$F = (\frac{1}{σ_{1}^{t}} - \frac{1}{σ_{1}^{c}}) σ_{1} + (\frac{1}{σ_{2}^{t}} - \frac{1}{σ_{2}^{c}}) σ_{2} + (\frac{1}{σ_{2}^{t}} - \frac{1}{σ_{2}^{c}}) σ_{3} + \frac{σ_{1}^{2}}{σ_{1}^{t} \cdot σ_{1}^{c}} + \frac{σ_{2}^{2}}{σ_{2}^{t} \cdot σ_{2}^{c}} + \frac{σ_{3}^{2}}{σ_{2}^{t} \cdot σ_{2}^{c}} - \frac{σ_{1} \cdot σ_{2}}{σ_{1}^{t} \cdot σ_{1}^{c}} - \frac{σ_{1} \cdot σ_{3}}{σ_{1}^{t} \cdot σ_{1}^{c}} + \frac{σ_{12}^{2}}{{\bar{σ}}_{12}^{2}} + \frac{σ_{31}^{2}}{{\bar{σ}}_{12}^{2}} \leq 1$

The criterion is considered to be reached when $F = 1$ . In fact, the damage variable corresponds to the criterion itself $D = F$ .
Once the criterion is reached $D = F = 1$ , two behaviors can be set up:
- If I_{fail_sh} = 0 or I_{fail_so} = 0, there is no stress softening and elements are never deleted. In this case, the failure criterion is purely visual using the output of the damage variable.
- If I_{fail_sh} ≠ 0 or I_{fail_so} ≠ 0, a stress relaxation is generated to decrease the load carrying capacity of the element.(3)
  $σ (t) = f (t) \cdot σ_{d} (t_{r})$
  
  With $f (t) = \exp (- \frac{t - t_{r}}{τ_{\max}})$ and $t \geq t_{r}$ .
  
  Where,
  
  $t$
  
  Time.
  
  $t_{r}$
  
  Start time of relaxation when the damage criteria is assumed.
  
  $τ_{\max}$
  
  Time of dynamic relaxation.
  
  $σ_{d} (t_{r})$
  
  Stress tensor when the criterion is reached.
  
  When the stresses reach 1% of the stress value at the beginning of the failure, the element is deleted. This is necessary to avoid instabilities coming from a sudden deletion of an element and a failure “chain reaction” in the neighboring elements. Even if the failure criterion is reached, there will be no element deletion with the default value of $τ_{\max} = 1.0 E 20$ . Therefore, it is recommended to define a value for $τ_{\max}$ 10 times larger than the simulation time step.
To avoid “chain reaction” when deleting elements, you can also define a stress tensor filtering frequency F_cut. Thus, the stress tensor used to calculate the HOFFMAN criterion is first be filtered according to:(4)
$σ_{n + 1}^{f i l t} = α σ_{n + 1} + (1 - α) σ_{n}^{f i l t}$

With $α = \frac{2 π \cdot F_{c u t} \cdot Δ t}{2 π \cdot F_{c u t} \cdot Δ t + 1}$

Where, $Δ t$ is the current timestep.

If a filtering frequency is not defined (F_cut= 0.0), the filtering effect is deactivated.
The fail_ID is used with /STATE/BRICK/FAIL and /INIBRI/FAIL. There is no default value. If the line is blank, no value will be output for failure model variables in the /INIBRI/FAIL (written in .sta file with /STATE/BRICK/FAIL option).