Multi-Domain Technique

The objective of the Multi-Domain technique (also referred to as RAD2RAD) is to optimize the computing performances of large scale Radioss models.

The objective of the Multi-Domain technique is to optimize the computing performances of large scale Radioss models that meet certain criteria:
  • Possibility of sub-dividing the whole model into a number of distinct subdomains with clearly defined interfaces/connections between them.
  • Different subdomains should be characterized by different mesh sizes and consequently very different minimum time step.

The goal is to improve prediction accuracy at reasonable, possibly advantageous, computation time for models with domains of very different time step sizes.

For example, it is appealing to use Multi-Domain technique to compute large models that have one or more parts finely meshed to capture specific local phenomena such as cracks localization/propagation.

It is even more appealing to use Multi-Domain technique to compute large fluid-structure interaction models, as in aircraft ditching or landing simulations, where fluid elements with high time steps are numerous compared to Lagrange structure elements with very small time steps.

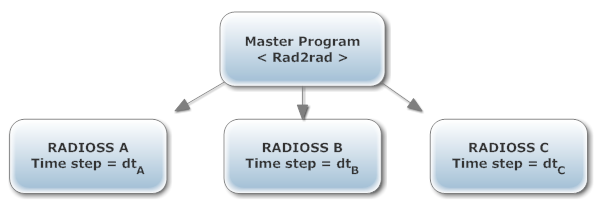
In the explicit integration scheme used by Radioss crash solver, the time step of the global model is penalized by the elements having the smallest time step. The concept is to replace this global model with physically equivalent subdomains, separating parts with different minimum time step. Each subdomain is resolved as a distinct Radioss model using its own time step, the force and momentum transfers between them being calculated by a separate main program (RAD2RAD), assuring stability constraints.


Figure 1.
Multi-Domain efficiency is based on two types of discrepancies:
  • Time step sizes
  • Domains relative sizes


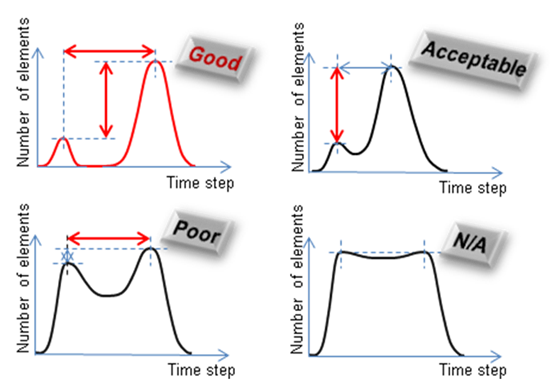
Figure 2.
It is particularly adapted to models with main and subdomains of:
  • very different mesh densities, hence very different time steps
  • different formulations like Lagrange, ALE or Lagrange, and SPH, provided the ALE or SPH domain is larger than the Lagrange domain