Isotropic / anisotropic materials

Introduction

The studied materials can be isotropic or anisotropic. In other words, the magnetic behavior of the material is as follows:

• independent of the direction of the applied field (isotropic material)
• dependent on the direction of the applied field (anisotropic material)

These two cases are presented in the following sections.

Isotropic materials

Isotropic materials are characterized by a magnetization law independent of the direction of the applied field.

The and vectors are always collinear.

The dependence between and is a scalar relationship, which is written as: J= σ.E or E= ρ.J

Anisotropic materials

Anisotropic materials are characterized by a law, which is dependent on the direction of the applied field.

The and vectors are not collinear.

The dependence between and is a vector relationship, which is written as: or

with σ conductivity tensor: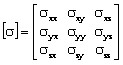

or ρ resistivity tensor: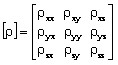

… in Flux

The model provided in Flux is a simplified model.

The vector dependence between and which is written as:

or can therefore be expressed:

• either under the form of three curves: J_x(E_x), J_y(E_y), J_z(E_z)

  The conductivity tensor is then written:

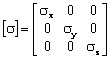
• or under the form of three curves: E_x(J_x), E_y(J_y), E_z(J_z)

  The resistivity tensor is then written: