Calculate the effect using all input variables simultaneously.
Multivariate effect of an input variable is the difference between the output
response values when the variable is at its lower and upper values while the
remaining variables are held constant. All calculations are based on a single linear
regression model including all variables.
Example
A system with two variables, X and Y and the output response, F (X,Y).
Table 1. Design Matrix
| Run |
X |
Y |
F (X, Y) |
| 1 |
42.0 |
108.0 |
1385.4 |
| 2 |
54.0 |
156.0 |
2290.2 |
| 3 |
66.0 |
84.0 |
3421.2 |
| 4 |
78.0 |
132.0 |
4778.3 |
| 5 |
32.4 |
165.6 |
824.4 |
| 6 |
44.4 |
93.6 |
1548.3 |
is the reference regression model and
intercept. A and coefficients, B and C, are calculated using the data set above.
A = - 2609.8
B = 88.6
C = 2.5
Regression equation:
- Effect of X (lower = 32.4, upper = 78.0)
Since we are investigating the
effect of X only, Y is held constant. For this example, use the mean
value (
= 123.2).
- X = 32.4, Y = 123.2
-
- X = 78, Y = 123.2
-
-
- Effect of Y (lower = 84, upper = 165.6)
Since we are investigating the
effect of Y only, X is held constant. For this example, use the mean
value (
= 52.8).
- X = 52.8, Y = 84
-
- X = 52.8, Y = 165.6
-
-
| Input Variable |
Multivariate Effect |
| X |
4040.4161 |
| Y |
202.7087 |
 (multiple
plots) and selecting the responses to plot using the Channel Selector.
(multiple
plots) and selecting the responses to plot using the Channel Selector.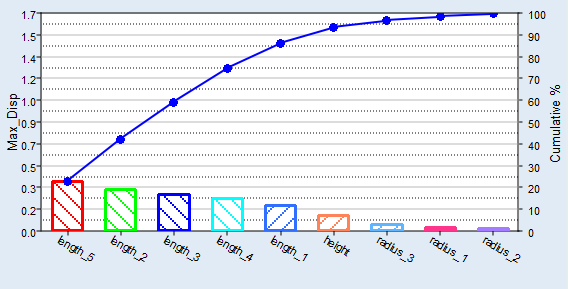
![]() (located in the top, right corner of the work
area). For more information about these settings, refer to Pareto Plot Tab Settings.
(located in the top, right corner of the work
area). For more information about these settings, refer to Pareto Plot Tab Settings.