Vibration and Acoustic Solutions

Acoustic Performance Analysis

To analyze optimum performance of speakers for high-quality sound with less noise, finite element analysis is performed.

Use-Case

Everyone wants great, high-quality, loud but clear sound from their audio system that fills the room with a deep bass and clear treble. The sound quality should not cause changes when the volume is turned up, and you certainly want to avoid vibrations, static hiss to come out of the speakers.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

FEA Model Description

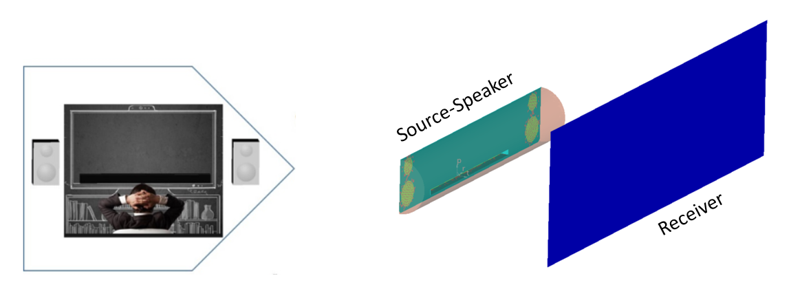
This model has a source plate (green in color) inside the speaker which is vibrating (unit displacement is applied as excitation) along the z-axis. The source plates are then covered with acoustic fluid elements (front, back and top), as shown in Figure 1. For pressure (as calculated on grids) contour, the receiver elements are configured with PLOTEL elements with fluid grids, since you will be capturing the sound pressure on these elements. A direct frequency response analysis is performed.


Figure 1. Speakers Acoustic Model

Results

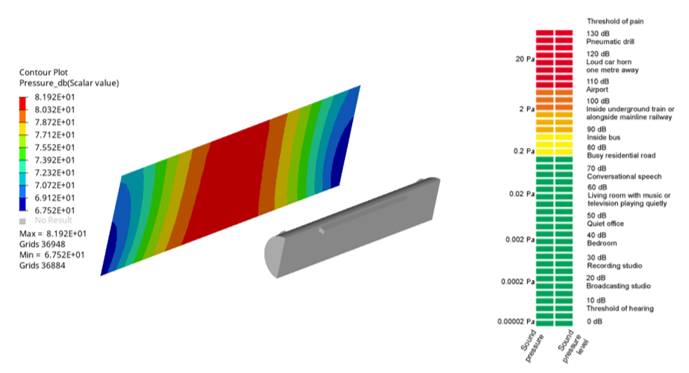
The pressure intensity on the receiver is 81 db, which can be referred to as loud sound of the speakers.


Figure 2. Pressure Intensity on the Receiver in db

Vibro-Acoustic Analysis

OptiStruct provides a simulation-driven approach for the design of speakers to perceive the best quality sound.

Today, the loud speaker industry has been making immense advances in the design of speakers. Speakers are becoming miniaturized, compact and smart. As they continue to minimize the size, yet compacted with electronics, physical testing of such small devices become very cumbersome and expensive. For example, due to high vibrations produced in the speakers, the inside components tend to hit each other and produce a buzz and/or rattle. If two small wires or two plates are continually hitting or rubbing each other, it is difficult to locate the problem site itself because of such a compact environment inside the speaker. OptiStruct provides a good solution to visualize and diagnose the problem. The results from the OptiStruct simulation can be used for the designing of speakers for optimum performance.

OptiStruct’s Vibration and Acoustic capabilities are used to perform various tests are:


Figure 3. Analysis Types Performed on Speaker Model


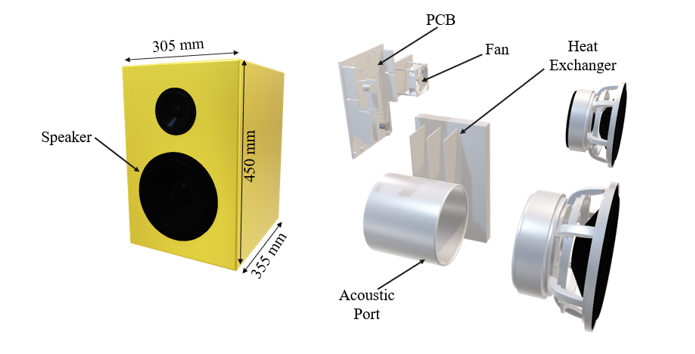
Figure 4. Speaker Model

Normal Modes Analysis

Use-Case

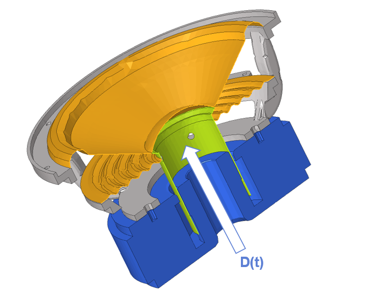
Figure 5 shows the complete geometry of the speaker. The load is applied to the voice coil which causes it to oscillate. Current is passed through the voice coil which produces its magnetic field. This magnetic field reacts with magnetic field of the permanent magnet which causes the voice coil to oscillate. The diaphragm is connected to voice coil which also oscillates, due to voice coil motion. Corrugations are provided on the suspension to enhance the high-frequency sensitivities of the model.


Figure 5. Physics of Speaker

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

FEA Model Description

The speaker model is constrained in all DOF’s at the 4 points (Figure 6). The goal of the modal analysis is to measure the natural mode shapes and frequencies of the speaker.


Figure 6. Modal Analysis - Model Setup

Results

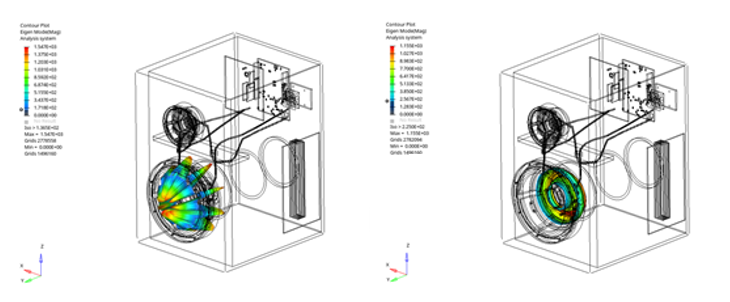
Mode shapes up to 2000 Hz are requested. You can visualize the model shapes of even the smallest component included in the speaker model (something which is difficult in real-life test).


Figure 7. Mode Shapes of the Speaker Membrane


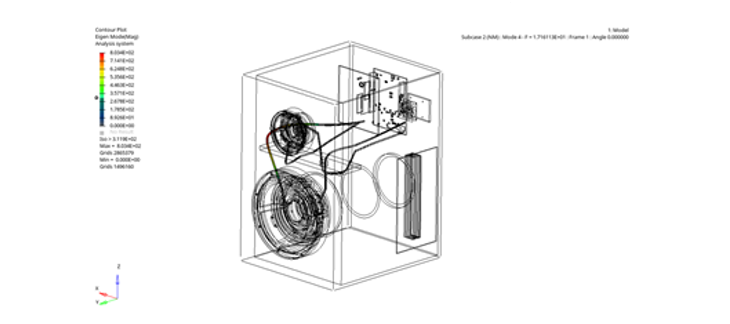
Figure 8. Mode Shapes of the Cables

Frequency Response Analysis

Used to calculate the steady-state response of the structure, due to sinusoidal load applied at a single frequency.

Use-Case

Frequency Response Analysis is performed on speakers to know the vibration levels of the speakers at different locations of the assembly. You can identify any violated targets, diagnose the root cause of the failures and then optimize to meet the target. Hence, use Frequency Response Analysis to catch any extreme vibrations and optimize the speaker design. OptiStruct provides an option (PFMODE) to check the modal participation factor for all modal frequency response subcases. In this way, you can see which structural modes contribute maximum towards the response of our target points.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

FEA Model Description

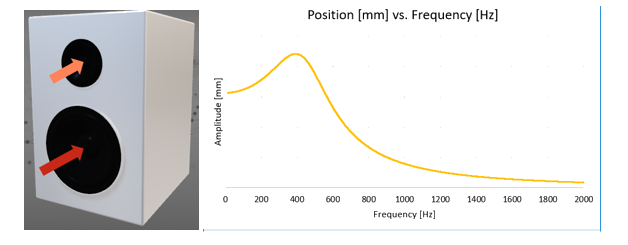
Apply excitation on the upper and lower voice coils to make the membrane vibrate. Request responses at specific locations in the assembly to check if the vibrations at these response points violate the target value. Also, look to find the modal participation factors for the response of PCB so you request a point on PCB.


Figure 9. Load Applied to Two Speaker Membranes
Multiple response points are located on PCB, speaker cabinet, heat exchanger, magnets and fan. Here, focus mainly on the response of PCB for this process. Track the acceleration of PCB to monitor the design, so as to keep the PCB acceleration below 50G.


Figure 10. Locations of the Response Points

Results

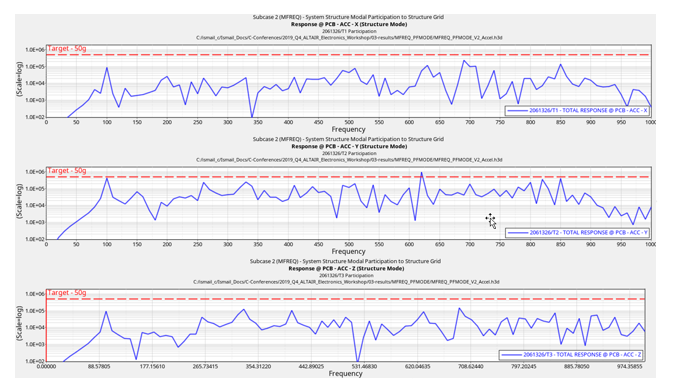
Investigate the vibration levels at different locations in the assembly but our main focus is the response of the PCB. The results for the PCB response point are shown in Figure 11. Frequency versus Acceleration is plotted in all three directions. Check for the frequencies where the acceleration value crosses the target value of 50G.


Figure 11. Response of PCB in X, Y and Z Direction
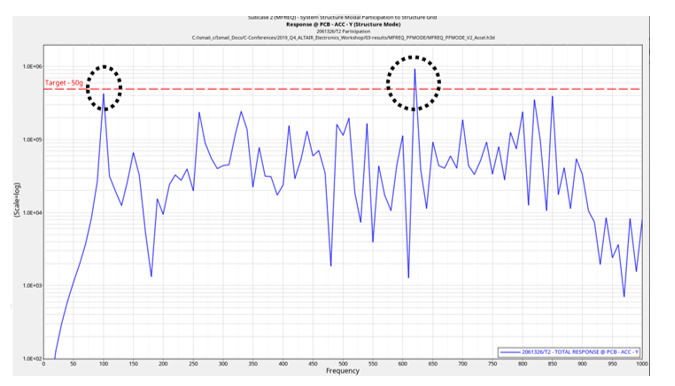
PFMODE function shows the modal participation factors contributing to these violated target values.


Figure 12. Violated Target at Two Frequencies


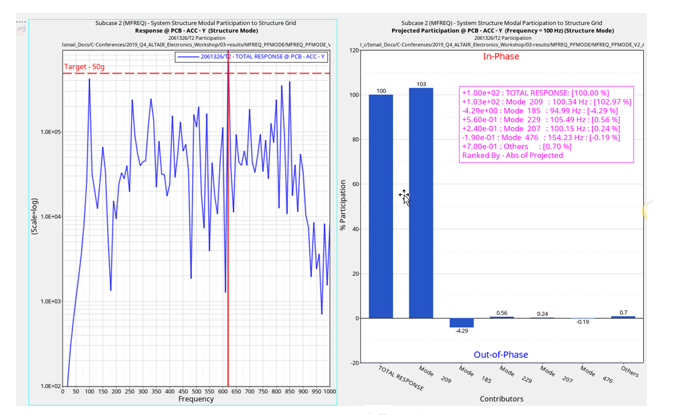
Figure 13. Modal Participation Factors for the Response in Y Direction

Transient Analysis

Identify the dynamic response of the speaker assembly when it is subjected to time-dependent load. The motto of Transient Analysis is to track the overall displacement of the speaker and to check the relative motion of the springs with respect to the stationary clamped table.

Use-Case

Here a Modal Transient Analysis in OptiStruct is performed to visualize the vibrating motion of the speaker assembly which is supported on springs.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

FEA Model Description

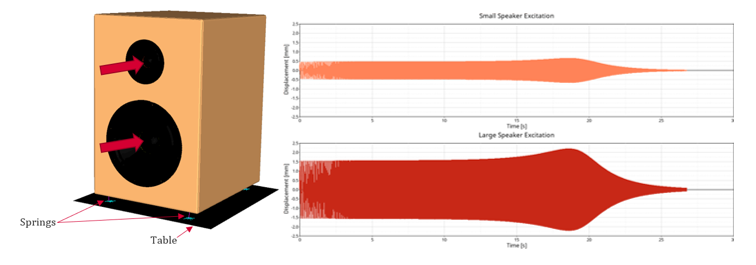
The bottom of the cabinet is attached to 4 springs, and the springs are resting on a fixed table (Figure 14). A transient load is applied to both membranes of the speaker.


Figure 14. Loading on the Speaker Assembly

Results



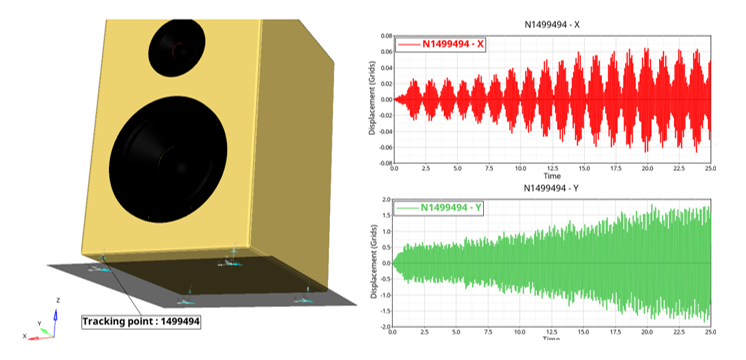
Figure 15. Displacement of Spring Elements

Acoustic Analysis

Acoustic modeling in infinite and semi-infinite domains is essential in the prediction of quantities such as external and radiated noise in vibro-acoustic problems. The different methods used for solving acoustic problems are described.

External Acoustic using Infinite Element Method: Use-Case

This method involves a smooth acoustic mesh (in this case, a sphere) around the structural mesh. The ends of the acoustic mesh are (surface of the acoustic sphere) have infinite elements.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

FEA Model Description

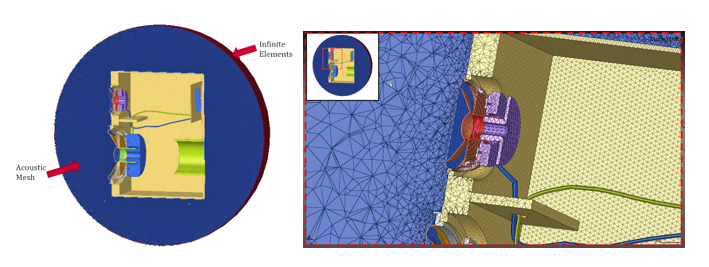
The speaker assembly is subjected to the load as was applied in Modal Frequency Analysis. The boundary conditions are the same in this scenario too. Here the speaker assembly is surrounded by the acoustic elements and infinite elements (Figure 16). The microphones are located at 1 m to measure the sound pressure level.


Figure 16. Acoustic Mesh with Infinite Elements

Results

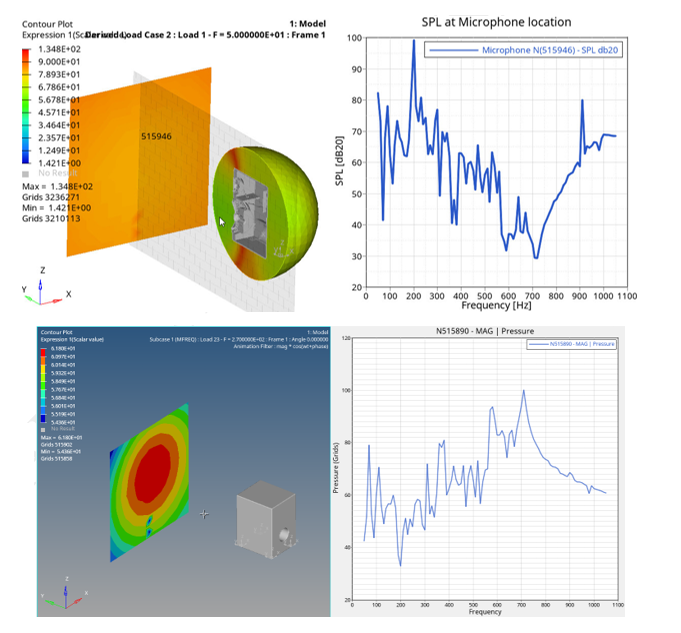
The pressure plot on the microphones located at a distance of 1m is:


Figure 17. Pressure Plots for Two Microphone Points (N515956 and N515890)

External Acoustic using RADSND Method

This method measures the radiated sound generated by vibrating nodes, assuming the nodes to be discrete acoustic sources.

Use-Case

This method does not require any acoustic mesh around the structure and; therefore, is faster to compute but the results obtained are approximate, not exact.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

FEA Model Description

The speaker assembly is subjected to the load as was applied in Modal Frequency Analysis. The boundary conditions are the same in this scenario too. The microphones are located at 1 m to measure the sound pressure level.

Results



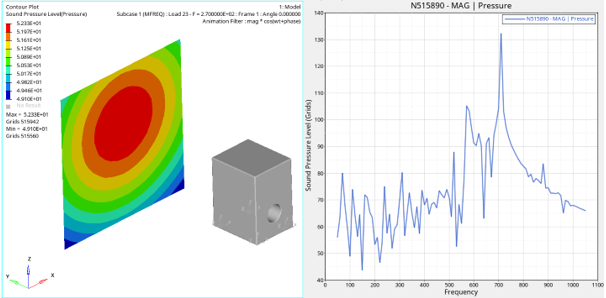
Figure 18. Pressure Plots for Microphone Point (N515890)

Performance of Speaker Model

Here the sound pressure levels, as perceived by a human in its natural environment, are tested.

Use-Case

A speaker arrangement in a living room is showcased, where you query the sound pressure levels at different locations in the room and also check the effect of the speaker assembly rotation on the perceived sound pressure levels. Here, you will exemplify how OptiStruct offers an efficient platform to test the speakers in real-life settings versus against a lab setting (Physical tests), where the microphones are located only at pre-defined points.

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

Model Description

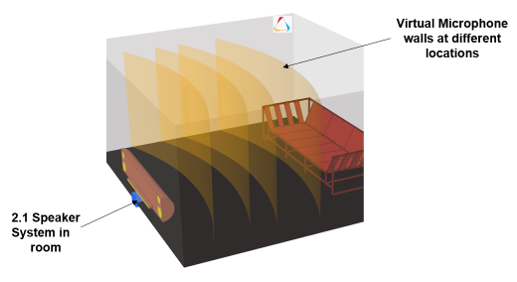
The speaker assembly is set in a standard living room of size 4m x 6m. Virtual microphones are placed at equal intervals (the microphones can be placed at any location in a room).


Figure 19. 15 Speaker Assembly in Living Room Setup
The speaker assembly is tested in two scenarios:
  1. Sound Pressure Levels when Speakers are directly facing the audience (angle = 0°)


    Figure 20. Speaker Assembly at 0°
  2. Sound Pressure Levels when Speakers are rotated (angle = 30°)


    Figure 21. Speaker Assembly at 30°

Results



Figure 22. Variation of the Sound Pressure Levels . across the walls and different sections of the room


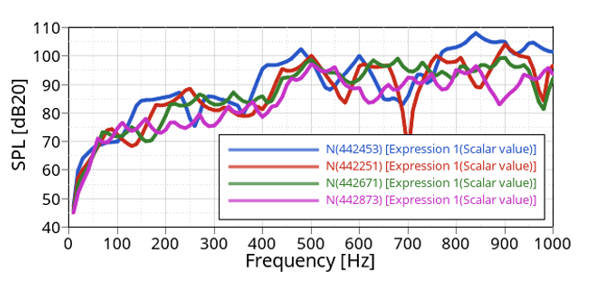
Figure 23. Sound Pressure Levels Comparison for 0° Speaker Orientation. at different locations in a living room setting


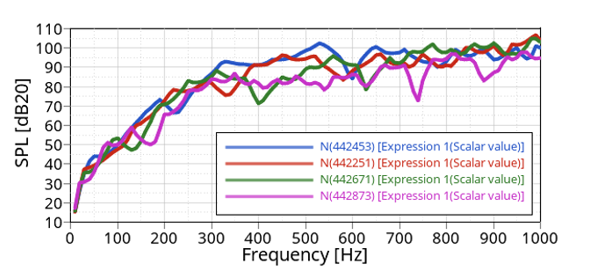
Figure 24. Sound Pressure Levels Comparison for 30° Speaker Orientation. at different locations of the room

Random Vibration Analysis

The structrual integrity is determined in this analysis.

PCBs are used in most electronic products to mechanically support and electrically connect chips, capacitors, resistors, or other electronic components via soldered joints. Since many of these products will experience loading environments that include vibration loading, it is vital to determine the structural integrity of the PCB and its components, due to these loads. This determination is often achieved using a random vibration finite element analysis. The basic failure modes of components mounted on PCBs, due to random vibration environment are the results of:
  • high acceleration levels
  • high stress levels
  • large displacement amplitudes

Model Files

Before you begin, copy the file(s) used in this example to your working directory.

Frequency Response Analysis Use-Case

To analyze the critical area of PCB, first normal mode analysis is performed to calculate natural frequencies in the PCB.

Frequency Response Analysis Model Description

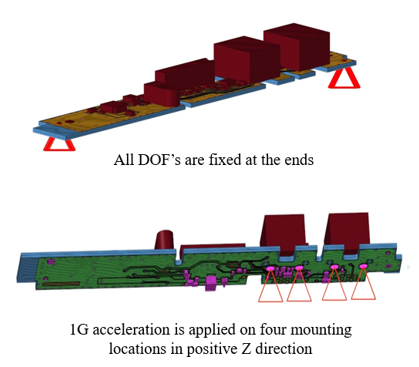
These frequencies are made as input for frequency response analysis and excitation of 1G acceleration is given to the PCB (Figure 25).


Figure 25. Frequency Response Analysis

Frequency Response Analysis Results



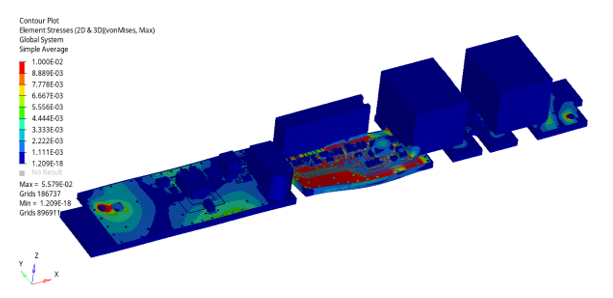
Figure 26. Maximum von Mises Stresses

Random Response Analysis Use-Case

Random Response Analysis is performed using results from FRF and adding a power spectral density graph of amplitude versus frequency up to 10000 HZ.

Random Response Analysis Results



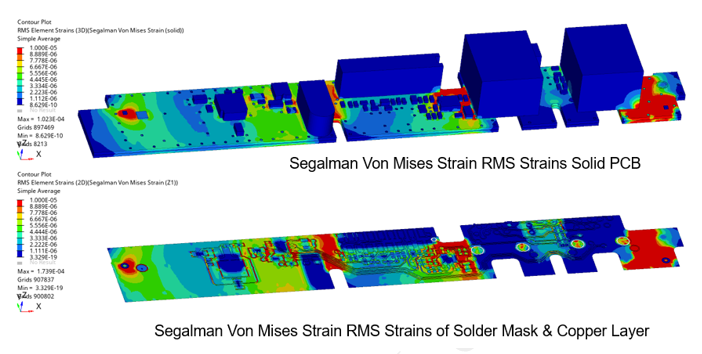
Figure 27. RMS Strains