/EOS/COMPACTION
Block Format Keyword Describes pressure for a porous media such as soil or foam which can be compacted and unloaded.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /EOS/COMPACTION/mat_ID/unit_ID | |||||||||
| eos_title | |||||||||
| C0 | C1 | C2 | C3 | Iform | |||||
| B | |||||||||
| Psh | |||||||||
Definition
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| eos_title | EOS title. (Character, maximum 100 characters) |
|
| C0 | EOS parameter. (Real) |
|
| C1 | EOS parameter. (Real) |
|
| C2 | EOS parameter. (Real) |
|
| C3 | EOS parameter. (Real) |
|
| Iform | Flag formulation for unloading behavior.
5
(Integer) |
|
| Elastic limit. No compaction below .
Default = 0.0 (Real) |
||
| Maximum compaction. Default = 1020 (Real) |
||
| B | Unloading bulk
modulus. (Real) |
|
| Psh | Pressure shift. (Real) |
Example
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
g mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW06/6/1
law06
# RHO_I
2.33e-3
# NU PMIN
0.22 -0.02
/EOS/COMPACTION/6/1
law06-compaction
# C0 C1 C2 C3 Iform
1E-2 0.256 0.256 1 1
# MUMIN MUMAX BUNL
0.0 0.115 1.44
# PSH
0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddataComments
- This equation of state is used to model pressure in porous media such as soil or
foam. The compaction has an elastic response when it is less than the elastic limit
.
Figure 1. - Plastic compaction is along path
defined by curve:
(1) Where,- Pressure in material
- Volumetric strain with
Unloading and reloading are made along straight line whose slope is B.- Psh
- Pressure shift value used to model the relative pressure formulation.
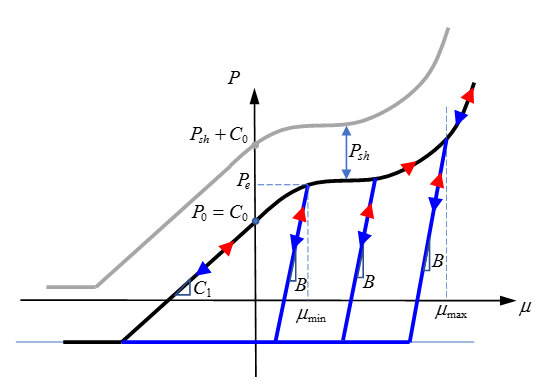
Figure 2. Pressure versus Volumetric Strain - In versions prior to 2019.1, this equation of state was embedded in /MAT/LAW10 with a fixed elastic limit, .
- Equations of state are used by
Radioss to compute the hydrodynamic pressure and are
compatible with the material laws:
- /MAT/LAW3 (HYDPLA)
- /MAT/LAW4 (HYD_JCOOK)
- /MAT/LAW6 (HYDRO or HYD_VISC)
- /MAT/LAW10 (DPRAG1)
- /MAT/LAW12 (3D_COMP)
- /MAT/LAW49 (STEINB)
- /MAT/LAW102 (DPRAG2)
- /MAT/LAW103 (HENSEL-SPITTEL)
- The unloading path runs along a
constant slope
by default. You can define a variable slope which increases
with the compaction using Iform=2. The slope will then evolve from C1 at
to
at
.
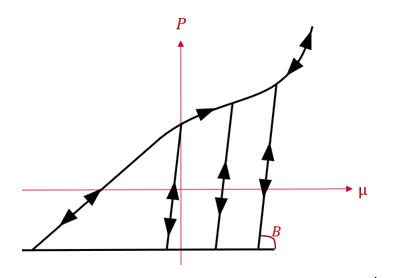 Figure 3. Iform=1 Unloading along a constant slope
Figure 3. Iform=1 Unloading along a constant slope
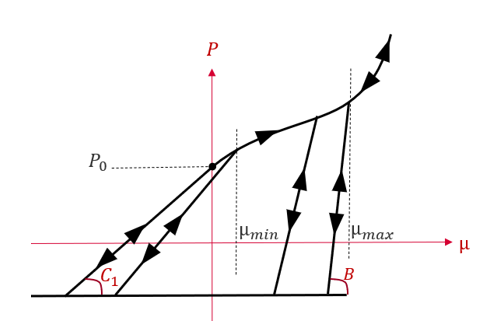 Figure 4. Iform=2 Unloading slope evolves from C1 to
in
Figure 4. Iform=2 Unloading slope evolves from C1 to
in