Bergstrom-Boyce (/MAT/LAW95)

This law is a constitutive model for predicting the nonlinear time dependency of elastomer like materials. It uses a polynomial material model for the hyperelastic material response and the Bergstrom-Boyce material model to represent the nonlinear viscoelastic time dependent material response.

This law is only compatible with solid elements.

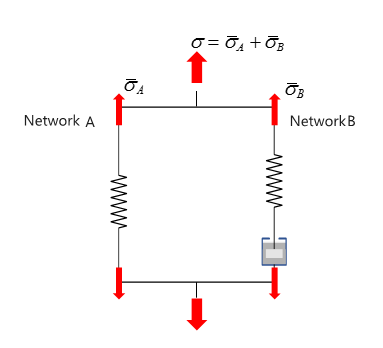
The response of the material can be represented using two parallel networks A and B. Network A is the equilibrium network with a nonlinear hyperelastic component. In Network B, a nonlinear hyperelastic component is in series with a nonlinear viscoelastic flow element, and hence, is time-dependent network.

Figure 1.

Material Parameters

The same polynomial strain energy density formulation is used for the hyperelastic components in both networks. In Network B, it is scaled by a factor

S_{b}

. The strain energy density is then written for the hyperelastic component of the network.(1)

W_{A} = \sum_{i + j = 1}^{3} C_{i j} {({\bar{I}}_{1} - 3)}^{i} \cdot {({\bar{I}}_{2} - 3)}^{j} + \sum_{i = 1}^{3} \frac{1}{D_{i}} {(J - 1)}^{2 i}

and(2)

W_{B} = S_{b} \cdot W_{A}

Where,

${\bar{I}}_{1} = {\bar{λ}}_{1}^{2} + {\bar{λ}}_{2}^{2} + {\bar{λ}}_{3}^{2}$
${\bar{I}}_{2} = {\bar{λ}}_{1}^{- 2} + {\bar{λ}}_{2}^{- 2} + {\bar{λ}}_{3}^{- 2}$
${\bar{λ}}_{i} = J^{- \frac{1}{3}} λ_{i}$
$C_{i j}$ and $D_{i}$: Material parameters

The hyperelastic component the Cauchy stress is computed as:(3)

σ_{i} = \frac{λ_{i}}{J} \frac{\partial W}{\partial λ_{i}}

The total stress is the summer of stress in network A and network B.

$σ = {\bar{σ}}_{A} + {\bar{σ}}_{B}$

Since $W_{B} = S_{b} \cdot W_{A}$ , then ${\bar{σ}}_{B} = S_{b} \cdot {\bar{σ}}_{A}$ and total stress is $σ = (1 + S_{b}) \cdot {\bar{σ}}_{A}$ .

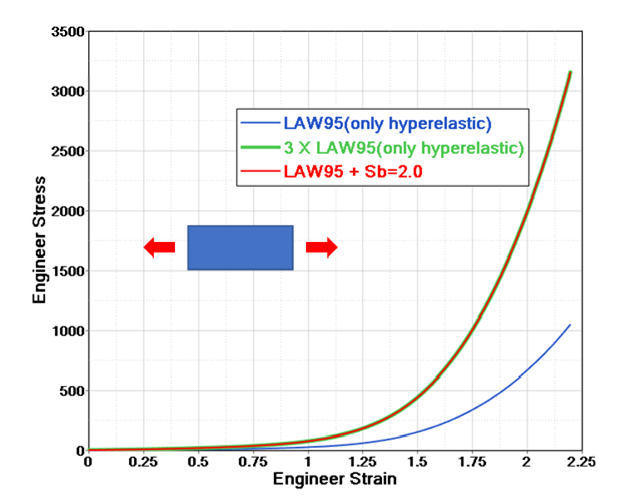
For example, in one tensile test. If use

S_{b} = 2

, the stress is 3 times of the one without considering viscous (which means only considered hyperelastic).

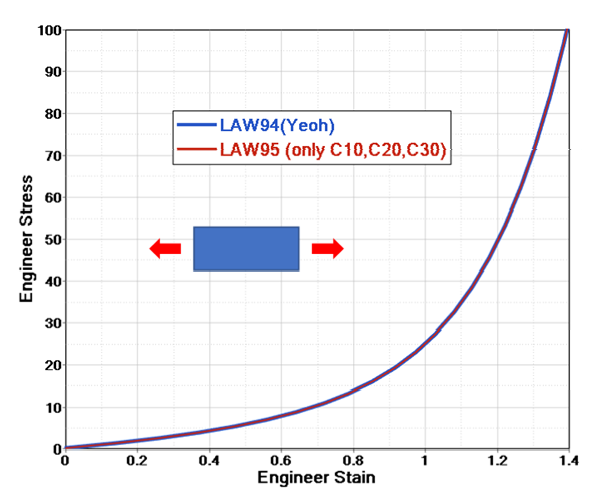
For special values of

C_{i j}

, the polynomial model can be reduced to the following material models.

Yeoh:
$j = 0$

Where, $C_{10}, C_{20}, C_{30}$ are not zero.

Figure 4.
Mooney-Rivlin:
$i + j = 1$

Where, $C_{10}$ and $C_{01}$ are not zero and $D_{2} = D_{3} = 0$ .
Neo-Hookean:
Only $C_{10}$ and $D_{1}$ are not zero.

Where,

$C_{i j}$ and $D_{i}$: Material parameters which can be calculated by completing a curve fit for quasi-static material test data.

RD-E: 5600 Hyperelastic Material with Curve Input, contains a curve fit example for Mooney-Rivlin and Yeoh material models. $D_{1}$ can be calculated from the bulk modulus or left blank.

The initial shear modulus and the bulk modulus are computed as:(4)

μ = 2 (S_{b} + 1) (C_{10} + C_{01})

and(5)

K = \frac{2}{D_{1}} (1 + S_{b})

If the bulk modulus of the material is known, $D_{1}$ can be calculated, or if $D_{1}$ =0, an incompressible material is assumed.

Viscous (Rate) Effects

The effective creep strain rate in Network B is given by:(6)

{\dot{ε}}_{B}^{v} = A {(\tilde{λ} - 1 + ξ)}^{C} {\frac{{\bar{σ}}_{B}}{τ_{r e f}}}^{M}

Where,

$\tilde{λ} = \sqrt{\frac{{\bar{I}}_{1}}{3}}$
${\bar{σ}}_{B}$: Effective stress in Network B.
$A, ξ, M, C$ , and $τ_{r e f}$: Input material parameters.

The material constants $A$ , $M$ and $C$ are limited to a specific range of real values as defined in the Reference Guide. If limited data is available, a trial and error method ¹ could be used to determine these constants. Start with the default values of $ξ, M, C$ , $S_{b}$ =1.6; and $A$ =5. Next, compare model predictions with experimental data for at least one strain rate and adjust $A$ to get a fit for the strain rate data.

References

¹ Bergström, J. S., and M. C. Boyce. "Constitutive modeling of the large strain time-dependent behavior of elastomers." Journal of the Mechanics and Physics of Solids 46, no. 5 (1998): 931-954