/MAT/LAW116

Block Format Keyword Describes mixed mode, strain rate dependent material model with damage and failure.

This material is only compatible with solid hexahedron elements (/BRICK) and the cohesive solid property (/PROP/TYPE43 (CONNECT)).

Note: Not compatible with any failure model. All damage and failure are defined inside of the material directly.

Format

(1)	(3)	(5)	(7)	(8)	(9)
/MAT/LAW116/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$ $ρ_{i}$
$E_{I}$ $E_{I}$	$E_{II}$ $E_{II}$	`Thick`	`Imass`	`Idel`	`Icrit`
$G C_{I_i n i}$ $G C_{I_i n i}$	$G C_{I_i n f}$ $G C_{I_i n f}$	${\dot{ε}}_{G_{I}}$ ${\dot{ε}}_{G_{I}}$	$f G_{I}$ $f G_{I}$
$G C_{I I_i n i}$ $G C_{I I_i n i}$	$G C_{I I_i n f}$ $G C_{I I_i n f}$	${\dot{ε}}_{G_{I I}}$ ${\dot{ε}}_{G_{I I}}$	$f G_{I I}$ $f G_{I I}$
$σ_{A_I}$ $σ_{A_I}$	$σ_{B_I}$ $σ_{B_I}$	${\dot{ε}}_{I}$ ${\dot{ε}}_{I}$	`I`_{order_I}	`I`_{fail_I}
$σ_{A_I I}$ $σ_{A_I I}$	$σ_{B_I I}$ $σ_{B_I I}$	${\dot{ε}}_{I I}$ ${\dot{ε}}_{I I}$	`I`_{order_II}	`I`_{fail_II}

Definition

Field	Contents	SI Unit Example
`mat_ID`	Material identifier. (Integer, maximum 10 digits)
`unit_ID`	Optional unit identifier. (Integer, maximum 10 digits)
`mat_title`	Material title. (Character, maximum 100 characters)
$ρ_{i}$ $ρ_{i}$	Initial density. (Real)	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
$E_{I}$ $E_{I}$	Young’s (stiffness) modulus in normal direction per unit length. (Real)	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
$E_{II}$ $E_{II}$	Shear (stiffness) modulus in tangent direction per unit length. Default = $E_{I I} = E_{I}$ $E_{I I} = E_{I}$ (Real)	$[\frac{P a}{m}]$ $[\frac{P a}{m}]$
`Thick`	Reference cohesive thickness. (Real)	$[m]$ $[m]$
`Imass`	Mass calculation flag. = 1 (Default) Element mass is calculated using density and mean area. = 2 Element mass is calculated using density and volume. (Integer)
`Idel`	Failure flag indicating the number of integration points to delete the element (between 1 and 4). Default = 1 (Integer)
`Icrit`	Yield and damage initiation flag. = 1 (Default) Based on quadratic nominal stress. = 2 Based on maximum nominal stress. (Integer)
$G C_{I_i n i}$ $G C_{I_i n i}$	Initial critical energy release rate for mode I (normal direction). (Real)	$[J]$ $[J]$
$G C_{I_i n f}$ $G C_{I_i n f}$	Upper bound of critical energy release rate. Indicates the strain rate dependency of $G C_{I}$ $G C_{I}$ . Default = 0.0 (Real)	$[J]$ $[J]$
${\dot{ε}}_{G_{I}}$ ${\dot{ε}}_{G_{I}}$	Reference (lower bound) strain rate for `GC` strain rate dependency. Must be defined if $G C_{I_i n f} > 0$ $G C_{I_i n f} > 0$ . (Real)	$[Hz]$ $[Hz]$
$f G_{I}$ $f G_{I}$	Shape factor for energy release rate before failure in mode I. (Real)
$G C_{I I_i n i}$ $G C_{I I_i n i}$	Initial critical energy release rate for mode II (shear). (Real)	$[J]$ $[J]$
$G C_{I I_i n f}$ $G C_{I I_i n f}$	Upper bound of critical energy release rate. Indicates the strain rate dependency of $G C_{I I}$ $G C_{I I}$ . Default = 0.0 (Real)	$[J]$ $[J]$
${\dot{ε}}_{G_{I I}}$ ${\dot{ε}}_{G_{I I}}$	Reference (lower bound) strain rate for `GC` strain rate dependency. Must be defined if $G C_{I I_i n f} > 0$ $G C_{I I_i n f} > 0$ . (Real)	$[Hz]$ $[Hz]$
$f G_{I I}$ $f G_{I I}$	Shape factor for energy release rate before failure in mode II. (Real)
$σ_{A_I}$ $σ_{A_I}$	Static yield stress in mode I. (Real)	$[Pa]$ $[Pa]$
$σ_{B_I}$ $σ_{B_I}$	Strain rate dependent yield stress term in mode I. (Real)	$[Pa]$ $[Pa]$
${\dot{ε}}_{I}$ ${\dot{ε}}_{I}$	Reference (lower bound) strain rate value for yield stress rate dependency in mode I. Must be defined $σ_{B_I} > 0$ $σ_{B_I} > 0$ . (Real)	$[Hz]$ $[Hz]$
`I`_{order_I}	Order of yield stress dependency on strain rate in mode I. = 1 (Default) Linear logarithmic dependency of strain rate. = 2 Quadratic logarithmic dependency of strain rate. (Integer)
`I`_{fail_I}	Failure criteria defined by $f G_{I}$ $f G_{I}$ : = 1 (Default) Ratio of fracture energy. = 2 Ratio of fracture displacements. (Integer)
$σ_{A_I I}$ $σ_{A_I I}$	Static yield stress in mode II. (Real)	$[Pa]$ $[Pa]$
$σ_{B_I I}$ $σ_{B_I I}$	Strain rate dependent yield stress term in mode II. (Real)	$[Pa]$ $[Pa]$
${\dot{ε}}_{I I}$ ${\dot{ε}}_{I I}$	Reference (lower bound) strain rate value for yield stress rate dependency in mode II. Must be defined if $σ_{B_I I} > 0$ $σ_{B_I I} > 0$ . (Real)	$[Hz]$ $[Hz]$
`I`_{order_II}	Order of yield stress dependency of strain rate in mode II. = 1 (Default) Linear logarithmic dependency of strain rate. = 2 Quadratic logarithmic dependency of strain rate. (Integer)
`I`_{fail_II}	Failure criteria defined by $f G_{I I}$ $f G_{I I}$ : = 1 (Default) Ratio of fracture energy. = 2 Ratio of fracture displacements. (Integer)

▸Example

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW116/3/1
MAT_COHESIVE_MIXED_MODE_ELASTOPLASTIC_RATE
#              RHO_I
              1.2E-9
#                 E1                  E2               Thick     Imass      Idel    Icrit  
                3000                1000               0.200         2         1        0
#            GC1_INI             GC1_INF              SRATG1                 FG1
               2.000               3.000               1.500                 0.7
#            GC2_INI             GC2_INF              SRATG2                 FG2
                9.00                   0                   0                 0.4
#              SIGA1               SIGB1              SRATE1   Iorder1    Ifail1
               33.00               1.500          2.50000E-5         1         2
#              SIGA2               SIGB2              SRATE2   Iorder2    Ifail2
               26.00               1.300          1.00000E-5         1         2
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata

Comments

The elastic stiffness is defined with:

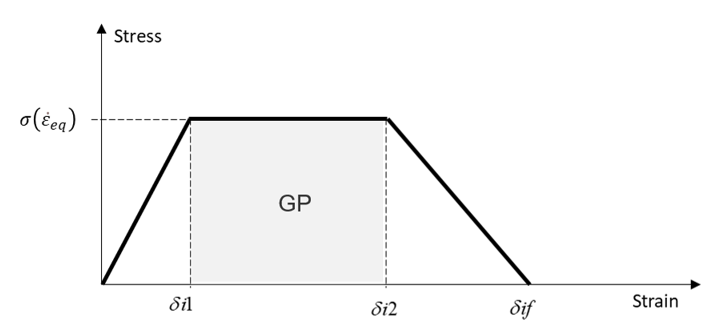
Figure 1.

Where,

GP

Plastic energy under constant stress

GC

Total energy

$i$ $i$ ={I,II}

The mode I (normal) and mode II (shear)
The shape of the traction separation law is defined with:
- Failure criteria defined by ratio of fracture energy (I_{fail_i}=1)(1)
  $0 \leq f G_{i} = \frac{G C_{i} ({\dot{ε}}_{e q})}{G C_{i} ({\dot{ε}}_{e q})} < 1 - \frac{σ {({\dot{ε}}_{e q})}^{2}}{2 G C_{i} ({\dot{ε}}_{e q}) E_{i}} < 1$ $0 \leq f G_{i} = \frac{G C_{i} ({\dot{ε}}_{e q})}{G C_{i} ({\dot{ε}}_{e q})} < 1 - \frac{σ {({\dot{ε}}_{e q})}^{2}}{2 G C_{i} ({\dot{ε}}_{e q}) E_{i}} < 1$
- Failure criteria defined by ratio fracture displacements (I_{fail_i}=2)(2)
  $0 \leq f G_{i} = \frac{δ_{i 2} - δ_{i 1}}{δ_{i f} - δ_{i 1}} < 1$ $0 \leq f G_{i} = \frac{δ_{i 2} - δ_{i 1}}{δ_{i f} - δ_{i 1}} < 1$
The yield stress is defined as:
- When I_{order_i}=1:(3)
  $σ ({\dot{ε}}_{e q}) = σ_{A_i} + σ_{B_i} . [\max (0, \ln (\frac{{\dot{ε}}_{e q}}{{\dot{ε}}_{i}}))]$ $σ ({\dot{ε}}_{e q}) = σ_{A_i} + σ_{B_i} . [\max (0, \ln (\frac{{\dot{ε}}_{e q}}{{\dot{ε}}_{i}}))]$
- When I_{order_i}=2:(4)
  $σ ({\dot{ε}}_{e q}) = σ_{A_i} + σ_{B_i} . {[\max (0, \ln (\frac{{\dot{ε}}_{e q}}{{\dot{ε}}_{i}}))]}^{2}$ $σ ({\dot{ε}}_{e q}) = σ_{A_i} + σ_{B_i} . {[\max (0, \ln (\frac{{\dot{ε}}_{e q}}{{\dot{ε}}_{i}}))]}^{2}$
  
  Where, $i$ $i$ ={I,II}, the mode I and mode II.
The equivalent strain rate is defined with:(5)
${\dot{ε}}_{e q} = \frac{\sqrt{{\dot{Δ}}^{2}_{I} + {\dot{Δ}}^{2}_{I I}}}{T h i c k}$ ${\dot{ε}}_{e q} = \frac{\sqrt{{\dot{Δ}}^{2}_{I} + {\dot{Δ}}^{2}_{I I}}}{T h i c k}$

Where,

${\dot{Δ}}_{I}$ ${\dot{Δ}}_{I}$

Normal velocity.

${\dot{Δ}}_{I I}$ ${\dot{Δ}}_{I I}$

Shear velocity.
The rate dependent fracture energies are defined with:(6)
$G C_{i} ({\dot{ε}}_{e q}) = G C_{i_i n i} + (G C_{i_\inf} - G C_{i_i n i}) . \exp (- \frac{{\dot{ε}}_{G_{i}}}{{\dot{ε}}_{e q}})$ $G C_{i} ({\dot{ε}}_{e q}) = G C_{i_i n i} + (G C_{i_\inf} - G C_{i_i n i}) . \exp (- \frac{{\dot{ε}}_{G_{i}}}{{\dot{ε}}_{e q}})$

Where, $i$ $i$ ={I,II}, the mode I and mode II.
Yield stress and damage law scheme:

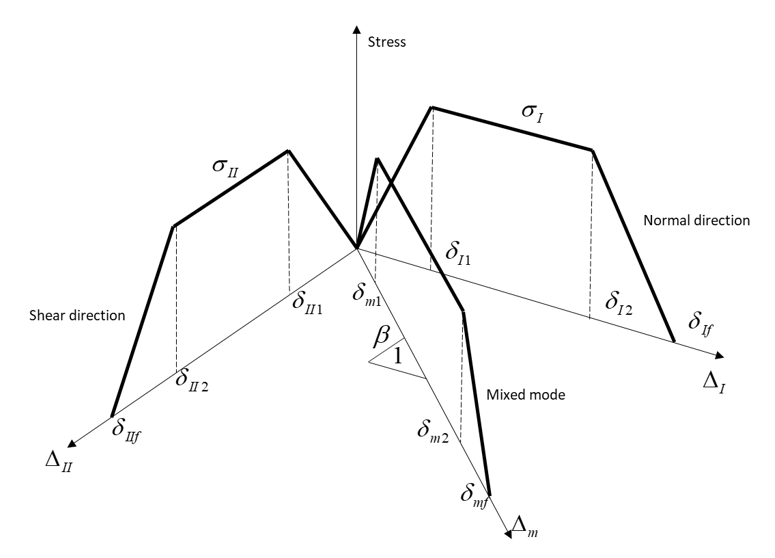
Figure 2.
For yield and damage based on quadratic nominal stress (Icrit=1):
- Mixed-mode yield initiation displacement is:(7)
  $δ_{m 1} = δ_{I 1} δ_{I I 1} . \sqrt{\frac{1 + β^{2}}{δ_{I I 1}^{2} + {(β . δ_{I 1})}^{2}}}$ $δ_{m 1} = δ_{I 1} δ_{I I 1} . \sqrt{\frac{1 + β^{2}}{δ_{I I 1}^{2} + {(β . δ_{I 1})}^{2}}}$
  
  Where,
  
  $δ_{i 1} = \frac{σ_{i}}{E_{i}}$ $δ_{i 1} = \frac{σ_{i}}{E_{i}}$
  
  $i$ $i$ ={I,II}, the mode I and mode II.
  
  $β = \frac{Δ_{I I}}{Δ_{I}}$ $β = \frac{Δ_{I I}}{Δ_{I}}$
- Mixed-mode damage initiation is:(8)
  $δ_{m 2} = δ_{I 2} δ_{I I 2} . \sqrt{\frac{1 + β^{2}}{δ_{I I 2}^{2} + {(β . δ_{I 2})}^{2}}}$ $δ_{m 2} = δ_{I 2} δ_{I I 2} . \sqrt{\frac{1 + β^{2}}{δ_{I I 2}^{2} + {(β . δ_{I 2})}^{2}}}$
  
  Where,
  
  $δ_{i 2} = δ_{i 1} + \frac{f G_{i} . G C_{i}}{σ_{i}}$ $δ_{i 2} = δ_{i 1} + \frac{f G_{i} . G C_{i}}{σ_{i}}$
  
  $i$ $i$ ={I,II}, the mode I and mode II.
For yield and damage based on quadratic nominal stress (Icrit=2).
- Mixed-mode yield initiation displacement is:
  If $β \leq \frac{δ_{I I 1}}{δ_{I 1}}$ $β \leq \frac{δ_{I I 1}}{δ_{I 1}}$ :(9)
  $δ_{m 1} = δ_{I 1} . \sqrt{1 + β^{2}}$ $δ_{m 1} = δ_{I 1} . \sqrt{1 + β^{2}}$
  
  If $β > \frac{δ_{I I 1}}{δ_{I 1}}$ $β > \frac{δ_{I I 1}}{δ_{I 1}}$ :(10)
  $δ_{m 1} = \frac{δ_{I I 1}}{β} . \sqrt{1 + β^{2}}$ $δ_{m 1} = \frac{δ_{I I 1}}{β} . \sqrt{1 + β^{2}}$
  
  Where,
  
  $β = \frac{Δ_{I I}}{Δ_{I}}$ $β = \frac{Δ_{I I}}{Δ_{I}}$
  
  $Δ_{I}$ $Δ_{I}$
  
  Displacement is mode I (normal).
  
  $Δ_{I I}$ $Δ_{I I}$
  
  Displacement is mode II (shear).
- Mixed-mode damage initiation is:
  If $β \leq \frac{δ_{I I 2}}{δ_{I 2}}$ $β \leq \frac{δ_{I I 2}}{δ_{I 2}}$ :(11)
  $δ_{m 2} = δ_{I 2} . \sqrt{1 + β^{2}}$ $δ_{m 2} = δ_{I 2} . \sqrt{1 + β^{2}}$
  
  If $β > \frac{δ_{I I 2}}{δ_{I 2}}$ $β > \frac{δ_{I I 2}}{δ_{I 2}}$ :(12)
  $δ_{m 2} = \frac{δ_{I I 2}}{β} . \sqrt{1 + β^{2}}$ $δ_{m 2} = \frac{δ_{I I 2}}{β} . \sqrt{1 + β^{2}}$
The mixed-mode final damage is (Icrit=1,2):(13)
$δ_{m f} = \frac{δ_{m 1} . (δ_{m 1} - δ_{m 2}) E_{I} G C_{I I} \cos^{2} γ + G C_{I} . (2 G C_{I I} + δ_{m 1} . (δ_{m 1} - δ_{m 2}) E_{I I} \sin^{2} γ)}{δ_{m 1} (E_{I} G C_{I I} \cos^{2} γ + E_{I I} G C_{I} \sin^{2} γ)}$ $δ_{m f} = \frac{δ_{m 1} . (δ_{m 1} - δ_{m 2}) E_{I} G C_{I I} \cos^{2} γ + G C_{I} . (2 G C_{I I} + δ_{m 1} . (δ_{m 1} - δ_{m 2}) E_{I I} \sin^{2} γ)}{δ_{m 1} (E_{I} G C_{I I} \cos^{2} γ + E_{I I} G C_{I} \sin^{2} γ)}$

Where,

$γ = \arccos (\frac{Δ_{I}}{Δ_{m}})$ $γ = \arccos (\frac{Δ_{I}}{Δ_{m}})$

$Δ_{m}$ $Δ_{m}$

Displacement is mixed mode.
The plastic strain is defined as:
- Mode I:(14)
  $Δ p_{I} = \max (Δ p_{I} (t - 1), Δ p_{I} - δ_{m 1} \cos γ, 0)$ $Δ p_{I} = \max (Δ p_{I} (t - 1), Δ p_{I} - δ_{m 1} \cos γ, 0)$
  
  Where, $(t - 1)$ $(t - 1)$ is the value from previous time step.
- Mode II:
  If $\sqrt{{(Δ_{I I - 1} - Δ p_{I I - 1} (t - 1))}^{2} + {(Δ_{I I - 2} - Δ p_{I I - 2} (t - 1))}^{2}} > δ_{m 1}$ $\sqrt{{(Δ_{I I - 1} - Δ p_{I I - 1} (t - 1))}^{2} + {(Δ_{I I - 2} - Δ p_{I I - 2} (t - 1))}^{2}} > δ_{m 1}$
  
  The plastic strain is computed for each direction 1 and 2 in the shear plane.(15)
  $Δ p_{I I - 1} = Δ p_{I I - 1} (t - 1) + Δ_{I I - 1} - Δ_{I I - 1} (t - 1)$ $Δ p_{I I - 1} = Δ p_{I I - 1} (t - 1) + Δ_{I I - 1} - Δ_{I I - 1} (t - 1)$
  (16)
  $Δ p_{I I - 2} = Δ p_{I I - 2} (t - 1) + Δ_{I I - 2} - Δ_{I I - 2} (t - 1)$ $Δ p_{I I - 2} = Δ p_{I I - 2} (t - 1) + Δ_{I I - 2} - Δ_{I I - 2} (t - 1)$
Stress value is reduced linearly from damage initiation to final damage ( $Δ_{m} > δ_{m 2}$ $Δ_{m} > δ_{m 2}$ ).(17)
$D = \max (\frac{Δ_{m} - δ_{m 2}}{δ_{m f} - δ_{m 2}}, D (t - 1), 0)$ $D = \max (\frac{Δ_{m} - δ_{m 2}}{δ_{m f} - δ_{m 2}}, D (t - 1), 0)$

The stress reduction is computed in the normal direction as:

If $Δ_{I} > Δ p_{I}$ $Δ_{I} > Δ p_{I}$ , then $σ_{I} = E_{I} (Δ_{I} - Δ p_{I})$ $σ_{I} = E_{I} (Δ_{I} - Δ p_{I})$ .

otherwise, $σ_{I} = E_{I} (1 - D) (Δ_{I} - Δ p_{I})$ $σ_{I} = E_{I} (1 - D) (Δ_{I} - Δ p_{I})$ .

For each direction 1 and 2 in the shear plane.(18)
$σ_{I I - 1} = E_{I I} (1 - D) (Δ_{I I - 1} - Δ p_{I I - 1})$ $σ_{I I - 1} = E_{I I} (1 - D) (Δ_{I I - 1} - Δ p_{I I - 1})$
(19)
$σ_{I I - 2} = E_{I I} (1 - D) (Δ_{I I - 2} - Δ p_{I I - 2})$ $σ_{I I - 2} = E_{I I} (1 - D) (Δ_{I I - 2} - Δ p_{I I - 2})$
The connection element is deleted when $Δ_{m} > δ_{m f}$ $Δ_{m} > δ_{m f}$ .