Local Reference Frame
- Global Cartesian fixed system
- Natural system , covariant axes x,y
- Local systems (x, y, z) defined by an orthogonal set of unit base vectors ( , , ). is taken to be normal to the mid-surface coinciding with , and ( , ) are taken in the tangent plane of the mid-surface.
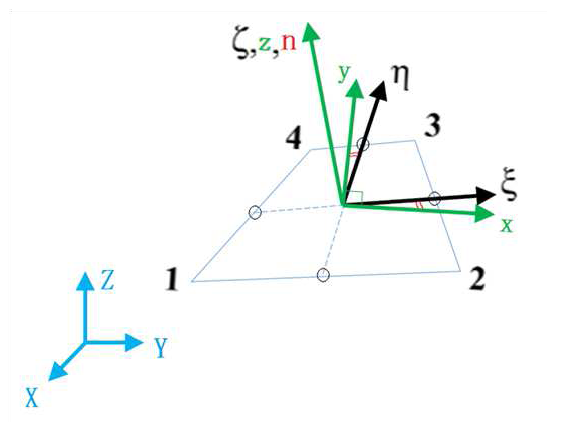
Figure 1. Local Reference Frame