Magnet (unidirectional): demagnetization curve (Hc, Br)
Presentation
This model ( Nonlinear magnet described by Hc and the Br module ) defines a nonlinear B(H) dependence with taking into account of demagnetization, wherever the curve knee is.
Main characteristics:
- the mathematical model and the direction of magnetization are dissociated
- a single material for description of several regions
Mathematical model
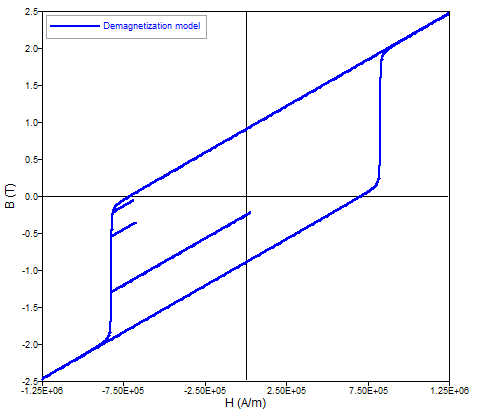
In the direction of magnetization the model is a combination of a straight line and an arc tangent curve.
The corresponding mathematical formula is written:
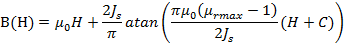
with: 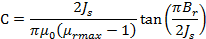
where:
- μ0 is the permeability of vacuum, μ0 = 4 π 10-7 (H/m)
- μrmax is the maximal relative permeability of material
- Br is the remanent flux density (T)
- Js is the saturation magnetic polarization (T)
The shape of the B(H) dependence in the direction of magnetization is given in the below figure:
In transversal directions one can write:
B⊥(H)= μ0μr⊥H⊥
where μr⊥ is the transverse relative permeability
Direction of magnetization
The various possibilities provided to the user are the same ones as those presented in § Magnet (unidirectional): linear approximation.
Demagnetization during solving
With this non-linear model, it is now possible consider the demagnetization during solving (i.e. the irreversible degradation of a magnet's remanent magnetic flux density due to its interaction with a demagnetizing field) by checking the specific option that is provided during the material creation. This demagnetization model is based on a static Preisach approach, and may apply in all quadrants of the magnet B(H) characteristic. The following additional remarks apply:
- Available for 2D and 3D in transient magnetic application
- In projects containing a magnet material with this option active, it is advisable to set the application to perform an initialization through a static calculation ().
- This model does not take in account temperature variations
- Delete the results;
- Go in and select: Initialization by static calculation;
- Create a new material Nonlinear magnet described by Hc and Br module;
- Check the option Taking in account demagnetization during solving;
- Assign the material to the regions representing the magnets in the project;
- Go to to define the direction of magnetization in the magnet;
- Solve the scenario.
- Select the desired time step;
- Create a new Arrows plot, then select the magnet as support;
- Then, in the formula editor, click on button Br Magnet (available in the
Magnetic Volume region tab) or type BrMagnet (without a space) in the
formula field.Note: In the formula editor, a related button Br is available and the user could also type the corresponding formula Br in the formula field. Remark that these recover the original remanent magnetic flux density stored in the material description, and not the remanent magnetic flux density modified by demagnetization effects at a given time step represented by BrMagnet.
In Flux, hard magnetic materials may be imported, exported and reused with the help of dedicated data exchange tools. These tools are notably useful when used in conjunction with magnets described by the B(H) property of type Nonlinear magnet described by Hc and the Br module, with the option for consideration of demagnetization during resolution. For a complete discussion on this topic, refer to the following documentation chapter: Import, export and reuse magnets.
Example of results
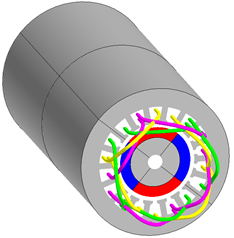
Figure 1. Full device
Figure 2. Arrow plots of the remanent magnetic flux density of one of the machine's magnet as a function of the control angle ψ.
Figure 3. Back E.M.F with and without demagnetization for ψ = π/4.