Free Surface Formulation

Standard SPH interpolation heavily depends on the basic premise that each particle has the so called full support. Full support implies that the owner particles can see particles all around itself within the smoothing length of the particle, which mathematically implies that the sum of the kernel, also known as Shepard coefficient, is equal to one.

(1)
S= 1 m b ∑ b ( V a 2 + V b 2 )W( r a − r b ,h )
Accurate reconstruction of the variable field depends on this principle. However, in a situation where you have a single phase flow, the particles on the free surface of the fluid are facing what is referred to as “particle vacuum” (absence of particles). In this situation layers of particles near to the surface begin to lose their full support, as shown in Figure 1.


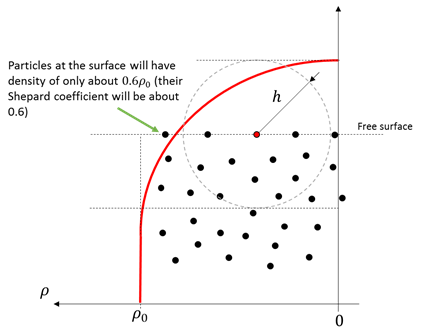
Figure 1. . Simplified sketch of a particles near a free surface losing their full support and consequent drop in density which leads to unphysical behavior.

Free surface switch (freesurface) enables a numerical treatment that prevents the artificial drop of density near a free surface which is facing the particle vacuum, therefore maintaining the physicality of the solution. Despite being designed for single-phase flows, it is strongly recommended to keep the freesurface switch set to true at all times.