粘着域のモデル化
粘着域のモデル化手法を使用して、接着および接合インターフェースおよび対応する亀裂発生や進展をモデル化できます。

図 1.
現在OptiStructでインターフェースをモデル化できる手法 / テクニックが複数存在します。粘着要素に依存する損傷に基づいた手法では、接着 / 接合インターフェースの板厚を考慮できます。他の手法 / テクニックでは、板厚効果が除外されます。テクニックという用語は、使用される要素タイプ(粘着要素と接触要素)を区別するために使用されます。
インターフェースの実装方法
粘着域は、層 / パートが樹脂または接着剤で結合される接着 / 接合インターフェースをモデル化するために使用されます。
- ポテンシャルベースの手法
- 損傷に基づいた手法
粘着域変形には3つのモードがあります。
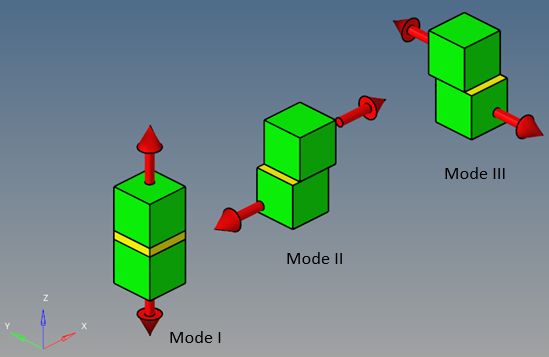
図 2.
図 2の座標系x-y-zは粘着域座標系です。PCOHEカードで指定されていない限り、その設定はCIFHEX/CIFPENバルクデータエントリで示されます。モードIはz方向の通常開口で、モードIIとモードIIIは、それぞれ、x-z平面とy-z平面内のせん断開口です。
接触では、接触ペアの2つの接線方向の特性は同じであると見なされます。そのため、モードIIとモードIIIの粘着特性は同じにすることをお勧めします。
ポテンシャルベースの手法(MCOHE)
ポテンシャルベースの手法では、3種類の曲線の中から引張力-開口量モデルが選択されます。
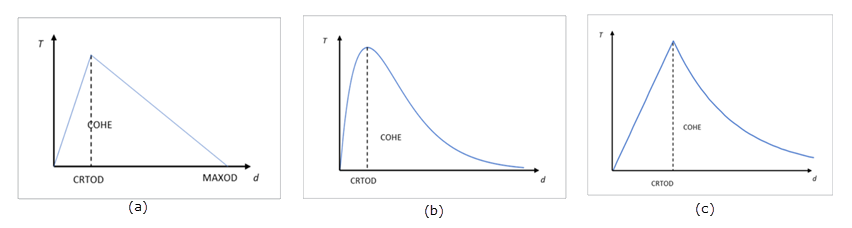
図 3. a)双一次、b)指数、c)線形指数
ポテンシャルベースの手法では、特定の接着または接合インターフェースのモデリングに、単一の粘着要素層のみを使用できます。
一般に、インターフェースにおける引張変形とせん断変形は、接着 / 接合の整合性や劣化を明らかにするうえで参考となります。圧縮での剛性は、MCOHEエントリのSFCフィールドを介して制御します。
- モードI、II、およびIIIの開口部。
- 混合係数。BETAフィールドに入力できます。
- 双一次:
(2) - 指数:
(3) - 線形指数:
(4)
- はCRTODです。
- はMAXODです。
- は組み合わされた相対変位()です。
また、線形指数曲線定義では、1つ以上のパラメータ、が必要です。これは、MCOHEカード内のフィールドEXPに入力されます。
損傷に基づいた手法(MCOHED)
損傷に基づいた手法を使用すると、接着 / 接合インターフェースの有限の板厚をモデル化することができます。これにより、実験データに基づいて粘着層をモデル化することが可能になります。
この手法では、亀裂成長が各要素内の損傷の進展によって制御されます。要素の損傷は、2つの指数、つまり、損傷開始指数と損傷進展指数によって制御されます。各要素では、2つの指数が最初は0です。荷重に伴って、損傷開始指数が増加します。損傷開始指数が1.0に達すると、損傷が現れます。その後は、損傷開始指数が1.0を維持し、損傷進展指数が増加し始めます。損傷進展指数が1.0に達すると、損傷が十分に大きくなり、その後は、粘着が失われます。こうして、亀裂が進みます。
損傷開始と損傷進展は、ユーザーがMCOHED、DMGINI(損傷開始)、およびDMGEVO(損傷進展)カードで定義したいくつかのパラメータによって制御されます。
モデル化テクニック(要素ベースまたは接触ベース)に応じて、CIFHEX/CIFPEN/PCOHEエントリまたはCONTACTインターフェースが必要です。モデリングテクニックをご参照ください。
MCOHEDエントリのKI、KII、およびKIIIフィールドで、3方向の弾性率 / ペナルティ剛性を定義できます。ここで、KIは法線方向用であり、KIIとKIIIは2つの接線方向用です。インターフェース内で、1つまたは複数の粘着要素層を定義できます。
一般に、インターフェースにおける引張変形とせん断変形は、接着 / 接合の整合性や劣化を明らかにする上で参考となります。要素に基づいたテクニックでは、圧縮時の剛性がMCOHEDエントリのSFCフィールドを介して制御されます。接触に基づいたテクニックの使用時は、圧縮時の剛性が接触プロパティによって決定されます。
要素に基づいたテクニックでは、粘着要素層の板厚がPCOHEのTHICKNESSフィールドを使用して定義できます。接触に基づいたテクニックでは、粘着域の板厚が内部的に1単位であると見なされます。
損傷に基づいた粘着モデルの以下の導入は、要素に基づいたテクニック用です。これらは、厚みが単位に置き換えられる場合は、接触に基づいたテクニックにも有効です。
要素に基づいたモデル化では、MCOHEDのDMGINIDおよびDMGEVOIDフィールドを使用して、必須のDMGINIおよびDMGEVOバルクデータエントリが指定されます。接触に基づいたモデル化の使用時は、圧縮での剛性は接触プロパティによって決定されます。
ポテンシャルベースの手法と同様に、上面と底面の節点間の相対変位が計算されます。まず、試行引張力の値(/)が、ペナルティ剛性(弾性率を量的な板厚で除算したもの)と3つのモードでの開口量を乗算することによって計算されます。
次に、DMGINIエントリのCRIフィールドで指定された基準を使用して、損傷開始が決定されます。
ひずみに基づいた開始基準
- 最大ひずみ値は、DMGINIエントリのV1、V2、V3フィールドで定義されます。
- 実際のひずみは、(相対変位を板厚で除算することによって算出されます。)
ここで、板厚はPCOHEのTHICKNESSフィールドで定義されます。
- 最大ひずみと実際のひずみの両方を使用し、次の式に基づいて損傷開始が決定されます:
- MAXE
-
(5) ここで、- = V1。
- = V2。
- = V3。
- QUADE
-
(6) ここで、- = V1。
- = V2。
- = V3。
応力に基づいた開始基準
- 最大応力値は、DMGINIエントリのV1、V2、V3フィールドで定義されます。
- 実際の応力は、対応する3方向それぞれの試行引張力の値です。
- 最大応力と実際の応力の両方を使用し、次の式に基づいて損傷開始が決定されます:
- MAXS
-
(8) ここで、- = V1。
- = V2。
- = V3。
- QUADS
-
(10) ここで、- = V1。
- = V2。
- = V3。
損傷開始基準が満たされなかった場合、損傷は発生しません。試行引張力は実際の引張力と等しくなります。したがって、亀裂の発生や伝搬は起こらず、対応する粘着関連の出力は結果ファイルに出力されます。
- 変位に基づいた損傷進展指数(DMGEVOエントリのTYPE=COHDISP)
- エネルギー散逸に基づいた損傷進展指数(DMGEVOエントリのTYPE=COHENRG)
どちらのタイプの損傷進展指数計算でも、引張力-開口量曲線の線形(SHAPE=LIN)形状または指数(SHAPE=EXP)形状をDMGEVOエントリで使用できます。
は、損傷進展指数(常に1.0以下)で、出力では、損傷指数として参照されます。
変位に基づいた損傷進展指数
SHAPE = LINの場合:
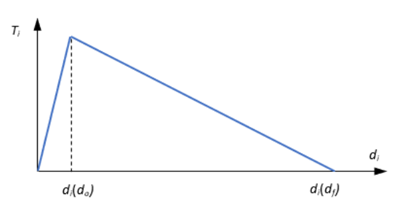
図 4.
SHAPE=EXPの場合
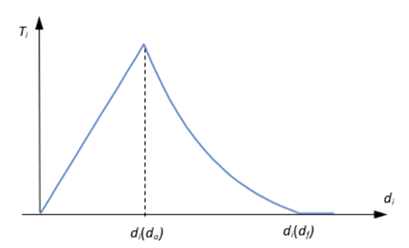
図 5.
- 履歴内の最大開口()。粘着域が載荷されるだけの場合は、は現在のと等しくなります。この値は、OptiStructによって計算され、各ステップで更新されます。粘着域が除荷もされる場合は、除荷領域内で、は履歴中で最大のと等しくなります(この値は、除荷開始前の値である可能性があるため)。
- 臨界開口(損傷が開始されたとき、すなわち亀裂発生基準が満たされたときの開口)。
- 最大開口()。
- DMGEVOエントリのW1フィールド。
- DMGEVOエントリのALPHAフィールド。
- 解析の各ステップにおける現在の開口。
エネルギー散逸に基づいた損傷進展指数
エネルギー散逸に基づいた損傷進展指数では、破壊靱性とも呼ばれる臨界総エネルギー( )が計算に使用されるキー値です。その計算と使用法は、曲線のタイプ(LIN/EXP)とモード混合法(MMXFM = 空白、1、2)に依存します。 は、破壊が発生する際のエネルギーを表します。
DMGEVOエントリのW1、W2、W3の各フィールドによって、3つの各破壊モードにおける臨界エネルギーが定義されます。
- 法線破壊モードI:
- W1 = (べき乗法則) = (Benzeggagh-Kenane(BK)形式)は、法線方向に破壊が発生する際の臨界エネルギーを定義します。
- せん断破壊モードII:
- W2 = (べき乗法則)は、モードIIで破壊が発生する際の臨界エネルギーを定義します。
- せん断破壊モードIII:
- W3 = (べき乗法則)は、モードIIIで破壊が発生する際の臨界エネルギーを定義します。
は、現在の解析ステップまでの総エネルギー(曲線の下の面積)です。
SHAPE = LINの場合:
- 履歴内の最大開口()。粘着域が載荷されるだけの場合は、は現在のと等しくなります。この値は、OptiStructによって計算され、各ステップで更新されます。粘着域が除荷もされる場合は、除荷領域内で、は履歴中で最大のと等しくなります(この値は、除荷開始前の値である可能性があるため)。
- 臨界開口(損傷が開始されたとき、すなわち亀裂発生基準が満たされたときの開口)。
- 解析でゼロの引張力が発生する開口。
- 亀裂発生基準が満たされたときの有効引張力。
- MMXFMフィールドが空白の場合:
(16) - MMXFMフィールドが1に設定されている場合(べき乗法則): は次の式によって得られます:
(17) ここで、、、およびは、DMGEVOエントリのW1、W2、およびW3フィールドです。の値は次の式によって得られます:(18) ここで、は、DMGEVOエントリのALPHAフィールドです。
- MMXFMフィールドが2に設定されている場合(BK形式):の値は、次の式に基づいています:
(19) ここで、- DMGEVOエントリのALPHAフィールド。
- および
- DMGEVOエントリのW1およびW2フィールド。
は、現在の解析ステップまでの総エネルギー(曲線の下の面積)です。
SHAPE=EXPの場合:
- 複合引張力。
- 粘着によって吸収される弾性エネルギー。これは、指数曲線の直線部分(損傷開始前)の下の面積です。
- 臨界開口(損傷が開始されたとき、すなわち亀裂発生基準が満たされたときの開口)。
- 最終開口。
- 現在の開口パターン下で粘着によって消散できる総エネルギー(、、およびの組み合わせ)。臨界エネルギーは、OptiStructによって自動的に計算され、モード混合形式(DMGEVOエントリのMMXFMフィールド)と、各モード(W1、W2、およびW3)で消散できるエネルギーに依存します。
- MMXFMフィールドが空白の場合:
(21) - MMXFMフィールドが1に設定されている場合(べき乗法則):は次の式によって得られます:
(22) ここで、- 、、および
- DMGEVOエントリのW1、W2、およびW3フィールド。
- 、、および
- 現在のステップまでの引張力-開口曲線の下のエネルギー。これらは、曲線のタイプ(LIN/EXP)に依存します。
ただし、デフォルトで、指数曲線では、の同じ値が線形曲線に使用されます。(23) - MMXFMフィールドが2に設定されている場合(BK形式):の値は:
(24) ここで、- DMGEVOエントリのALPHAフィールド。
- および
- DMGEVOエントリのW1およびW2フィールド。
は、現在の解析ステップまでの総エネルギー(曲線の下の面積)です。
実際の引張力の計算
実際の引張力は、前のセクションで説明した損傷進展指数の計算に基づいて、次のように計算されます。
- および
- モードに対応する弾性率と開口。
- PCOHEエントリで定義される板厚。
この実際の引張力は、後で解析に使用されます。
粘着要素の破壊
いずれかの粘着要素内の全積分点の損傷進展指数が、MCOHEDカードのMXDMGフィールドで定義された値に達し、これらの積分点のいずれも圧縮状態にない場合、その粘着要素は破壊され、現在のサブケースおよび継続サブケース内の残りの解析では機能しなくなります。
また、解析中に侵食された要素は、侵食された時点からH3D出力に表示されません。
モデリングテクニック
- 要素に基づいたテクニック(CIFHEX/CIFPEN要素)
- 接触に基づいたテクニック(CONTACTエントリ)
要素に基づいたテクニック(CIFHEXおよびCIFPEN要素)
- CIFHEX要素とCIFPEN要素が主に焦点を置くのは、上面と底面の間の相対移動です。
- 3つの方向(要素X、Y、Z)それぞれの各積分点における上面と底面の節点間の相対変位によって、粘着開口量が決定されます。
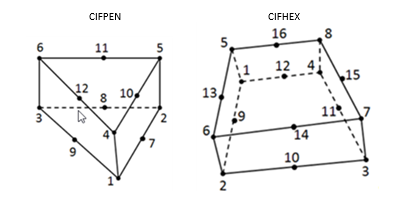
図 6. - 引張力によって引張剛性とせん断剛性が与えられ、PCOHEエントリのSFCフィールドによって粘着要素の圧縮剛性が指定されます。注: 引張力の計算は、接着 / 接合インターフェースのモデル化に使用される手法に依存します。
- 粘着要素の定式化の詳細については、インターフェース要素をご参照ください。
- 亀裂進展の経路内に粘着要素を挿入する必要があります。
- ポテンシャルベースの手法では、単一の粘着要素層のみを使用する必要があります。
- 損傷に基づいた手法では、複数の粘着要素層を使用できます。
- 粘着要素のモデル化には、CIFHEX要素とCIFPEN要素を使用できます。
- 粘着要素は、ベースモデルのシェル要素またはソリッド要素のみに結合できます。
- ベースモデルのシェル / ソリッド結合層と粘着要素層の間で、メッシュ密度がまったく同じ1対1の節点対応関係が存在する場合は、それらの節点を共有(結合)することができ、接触定義は不要です。
- このような正確な1対1の節点対応関係がない場合は、CONTACT(FREEZE)結合またはTIE結合を使用して、上面層または底面層の粘着要素をベースモデルの対応するシェル / ソリッド要素に結合する必要があります。
- 粘着要素は、インターフェース内に形状的板厚を有していることがあります。ポテンシャルベースの手法では、幾何学的な板厚に関係なく、自動的に単位板厚が内部的に使用されるため、板厚効果が除外されます。損傷に基づいた手法では、PCOHEのTHICKNESSフィールドを使用して板厚の解釈を制御できます。実際の値を使用することが重要です。デフォルト値は1.0に設定されます。
- 一部のケースでは、粘着要素で収束を得るのが難しい場合があります。粘着要素に減衰安定化を導入することで、収束を促進できます。減衰安定化は、MCOHEおよびMCOHEDエントリのVEDで定義できます。現時点では、粘着接触で減衰安定化を使用することはできません。
接触に基づいたテクニック(CONTACTエントリ)
接触に基づいたテクニックでは、粘着域のモデル化に粘着要素(CIFHEX/CIFPEN)を使用する必要はありません。このテクニックにより、粘着要素のメッシングおよび設定が不要になるため、モデル設定を簡素化できます。
CONTACTバルクデータエントリのCOHE継続行を使用して、接触に基づいた手法を粘着域モデル化に対してアクティブ化できます。MCOHEDIDフィールドではMCOHEDの識別番号が参照され、その結果として接触インターフェースが接着 / 接合インターフェースとして識別されます。
接触に基づいたテクニックでは、損傷に基づいた手法のみを使用できます。また、このテクニックの場合は、粘着域の板厚は内部で常に単位に設定されます。つまり、板厚効果は除外されます。
圧縮での貫通を回避するには、接触ペナルティを使用します。開口では、粘着効果がアクティブになり、接触効果が無視されます。
現在、粘着モデリングでサポートされているのは、SMALLのスライディング接触、無摩擦接触、N2S/S2S接触のみです。
サポートされるソリューションシーケンス
- 非線形静解析(SMDISPとLGDISP)
- 非線形過渡解析(SMDISPとLGDISP)
- 粘着要素では質量は考慮されません。
- 静解析、過渡解析、座屈解析、固有モード解析を含む線形解析
- 線形解析では粘着効果を使用できません。
- 線形解析では、粘着要素の初期剛性が使用されます。初期剛性は、MCOHEエントリまたはMCOHEDエントリ(MCOHEエントリで定義された引張力-開口量曲線の初期勾配またはMCOHEDエントリで定義されたKi値)によって決定されます。
- 亀裂の進展/ 開始は起こりません。
- 線形解析では、粘着要素関連の出力はありません。
- 粘着要素は現在、陰解法解析のみでサポートされています。陽解法解析はサポートされていません。
出力
粘着域からの出力は、現在はH3Dフォーマットのみに対応しています。
- 粘着損傷開始指数
- 損傷開始指数は、粘着要素の中心で計算されます。各粘着要素の損傷開始指数は、現在の要素状態がそのピーク引張からどれだけ離れているのかを示します。
- 粘着損傷開始指数の値が1.0に達すると、要素の損傷が開始したと見なされます。この時点で、粘着損傷指数は0.0を上回り始めます。
- このアイテムは、粘着要素と粘着接触のセカンダリサーフェスに表示されます。
- 粘着損傷指数(損傷進展指数)
- この値は粘着要素ごとに計算され、対象要素の損傷が開始すると(すなわち、粘着損傷開始指数が1.0に達すると)、0.0を上回り始めます。
- このアイテムは、粘着要素と粘着接触のセカンダリサーフェスに表示されます。
- モード別の単位面積当たりの粘着エネルギー(モード別の単位面積当たりの消散粘着エネルギー)
- これは、各モードの引張力-開口量曲線の下方の面積です。
- 単位面積当たりの粘着エネルギーは、3つのモード(モードI、II、III)で出力されます。
- このアイテムは粘着接触では得られません。
- モード別の粘着エネルギー(モード別の消散粘着エネルギー)
- これは、“モード別の単位面積当たりの粘着エネルギー”に、対応する粘着要素の表面積を乗算した値です。
- 粘着エネルギーは、3つのモード(モードI、II、III)で出力されます。
- このアイテムは粘着接触では得られません。
- 履歴中で最大の粘着開口量(最大開口量)
- これは、荷重履歴で最大の開口量です。
- このアイテムは粘着接触では得られません。
- 粘着開口量
- o これにより、3つのモード(局所要素座標系に沿ったモードI、II、III)と基準座標系における開口量の出力が得られます。
- このアイテムは粘着接触では得られません。
- 粘着ステータス(ステータス)
- 要素の載荷 / 除荷 / 破壊状態を示します。
- 0:荷重
- 1:除荷 / 再載荷
- 2:破壊
- このアイテムは粘着接触では得られません。
- 粘着引張力(引張力)
- これにより、局所要素座標系(モードI、II、およびIII)と基準座標系での引張力の出力が提供されます。
- このアイテムは粘着接触では得られません。
- 剥離成長指数(スカラー)
- 粘着要素のエネルギーをこの要素が破壊(つまり、要素が引張力-開口量曲線の終端に達する)されずに耐えられるエネルギーで除算した比率を表します。
- この結果は、特定の要素について損傷が発生し始めたときにのみゼロ以外となります。
- このアイテムは粘着接触では得られません。
浸食された粘着要素は、要素の浸食解析時刻以降のh3d出力には表示されません。したがって、上記のアイテムは浸食された粘着要素では得られません。詳細については、粘着要素の破壊をご参照ください。
粘着域のモデル化に接触が使用される場合は、出力が次のように解釈されます。粘着引張力と粘着開口量は、‘Contact Traction / Normal’、‘Contact Traction / Tangent’、‘Contact Deformation / Normal’、および‘Contact Deformation/Tangent’というラベルでリストされます。これを接触圧力と整合させるため、‘Contact Traction / Normal’では粘着法線引張力は負の値として表示されます。