boxplot
Creates a box plot. Returns the statistics of the input data and the handles of the graphics object.
Syntax
boxplot(data)
boxplot(data, group)
boxplot(data, notch, symbol, orientation, whisker, ...)
boxplot(data, group, notch, symbol, orientation, whisker, ...)
boxplot(data, options)
boxplot(data, group, options)
[s, h] = boxplot(...)
Inputs
- data
- Input sample. data can be a matrix where each column is a dataset, or, a cell of matrices.
- group
- If data is a vector, group may be used to group data. group must be a vector with the same length as data.
- notch
- Controls the notch of the box. The notch displays the confidence interval around the median. Typical values are in range [0, 1]. The default value is 0.
- symbol
- The display symbol for the outlier values. The default values are '+' for outliers between whisker*IQR and 2*whisker*IQR and 'o' for outliers > 2*whisker*IQR.
- orientation
- Sets the orientation of the box plot. Valid values are 0 for horizontal and 1 for vertical. Default value is 1.
- whisker
- Controls the length of the whiskers as a multiplier of IQR. Default value is 1.5.
- options
- The following options may be used to change the appearance of the box plot:
- 'boxstyle'
- Specifies the style of the box. Valid values are 'outline' (default) and 'filled'.
- 'boxwidth'
- Specifies the box width. Valid values are 'proportional' (default) and 'fixed'..
- 'capwidths'
- Specifies the width of the whisker cap. The width is calculated as 'capwidths'*'widths'/4. Default value is 1.
- 'colors'
- Specifies the color of each box. Can be a Nx3 matrix or a string.
- 'labels'
- Specifies the name of each group of elements. Must be a cell of strings.
- 'notch'
- Specifies the notch of the box. Valid values are 'on' (notch value is 0.25), 'off' (default) or a scalar value.
- 'orientation'
- Specifies the orientation of the boxes. Valid values are 'horizontal' (or 0) and 'vertical' (or 1, default).
- 'outliertags'
- Display or not the outlier index next to the outlier symbol. Valid values are 'on' and 'off' (default).
- 'positions'
- Specifies the position of each dataset on the X axis. Must be a vector with length equal to the number of datasets.
- 'sample_ids'
- Specifies a string id for each element. Must be a cell of cells. Each nested cell must be a cell of strings containing the ids of elements in a dataset.
- 'symbol'
- Specifies the outliers symbol. If one symbol is given, for example '^', then the outliers between whisker*IQR and 2*whisker*IQR will be displayed using this symbol. If two symbols are given, for example ['^', 'v'], then the second symbol will be used to display outliers > 2*whisker*IQR.
- 'whisker'
- Specifies the length of the whiskers as a multiplier of IQR. Default value is 1.5.
- 'widths'
- Specifies a scaling factor for the box widths. Default value is 0.4.
Outputs
- s
- A 7xN matrix containing statistics for each dataset. The matrix rows are:
- Minimum
- 1st quartile
- Median
- 3rd quartile
- Maximum
- Lower confidence limit for the median
- Upper confidence limit for the median
- h
- A struct with the handles of the graphics object. The struct contains the following fields:
- 'box'
- 'box_fill'
- 'labels'
- 'median'
- 'out_tags'
- 'out_tags2'
- 'outliers'
- 'outliers2'
- 'whisker'
Examples
clf;
mat = randn(100,4);
[s, h] = boxplot(mat);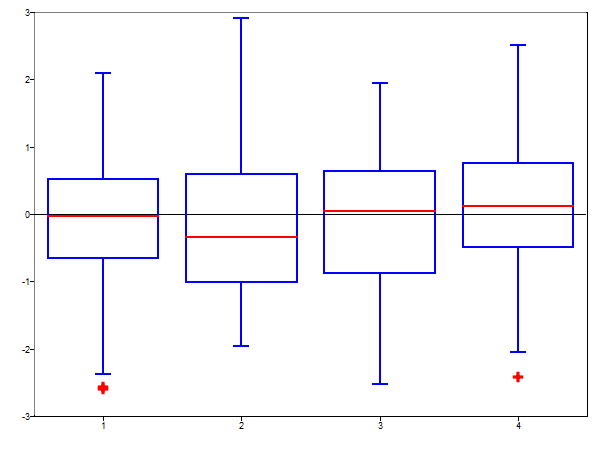
Figure 1. Box plot
clf;
mat = randn(400,1);
groups = [ones(1, 50), 2*ones(1, 250), 3*ones(1, 100)];
[s, h] = boxplot(mat, groups, 'capwidths', 2, 'symbol', '^');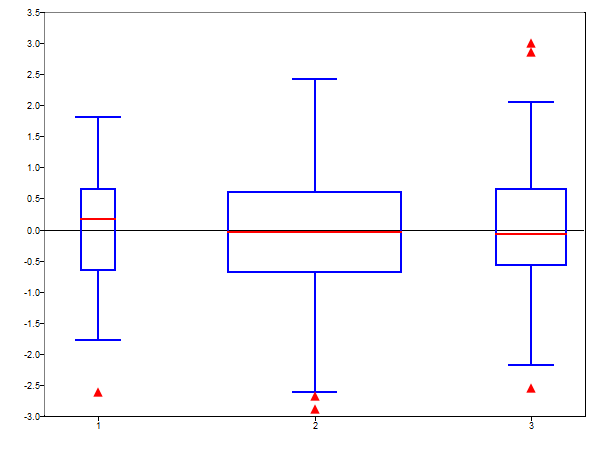
Figure 2. Dataset groups
clf;
cellIn = {randn(100,1), randn(100,2), randn(300,1)};
% set the notch, symbol, orientation and whisker values
[s, h] = boxplot(cellIn, 0.4, 'x+', 'horizontal', 1.6 );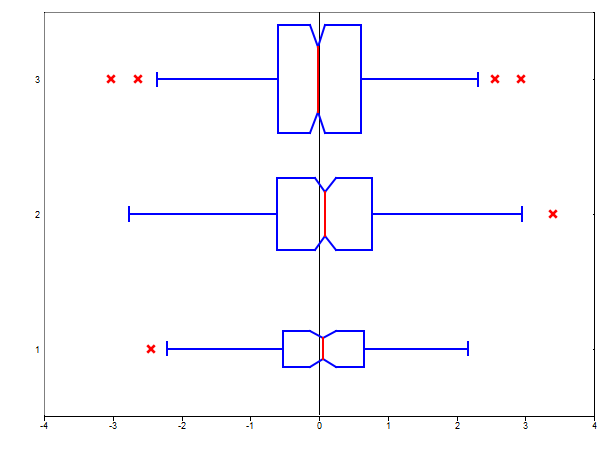
Figure 3. Cell input
clf;
mat = randn(100,10);
[s, h] = boxplot(mat, 'boxstyle', 'filled', 'colors', viridis(10));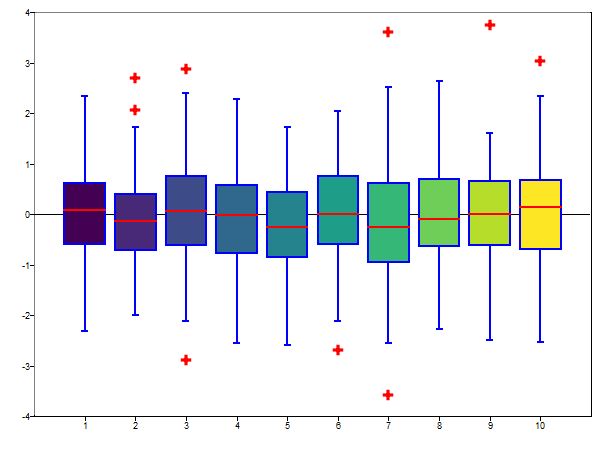
Figure 4. Box plot colors
clf;
mat = randn(100,4);
[s, h] = boxplot(mat, 'labels', {'A', 'B', 'C', 'D'}, 'outliertags', 'on');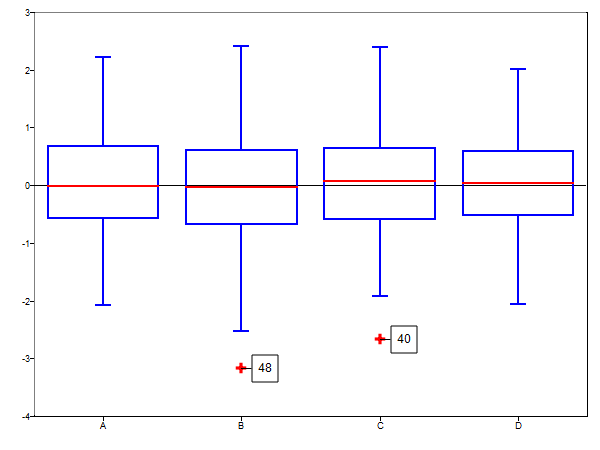
Figure 5. Custom x labels, display outlier tags
clf;
mat = randn(100,4);
[s, h] = boxplot(mat);
set(h.whisker,'linestyle','--');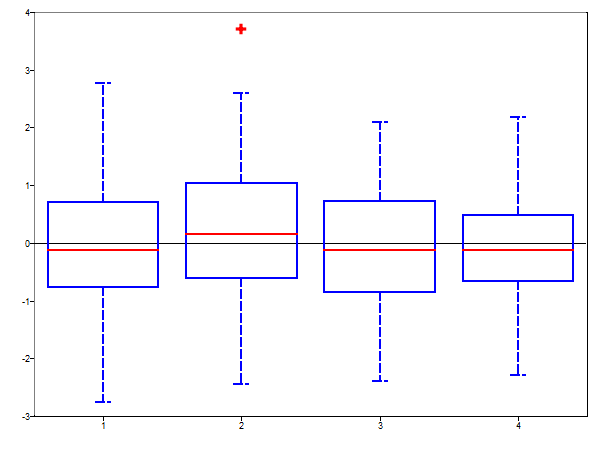
Figure 6. Change the whisker line style
Comments
If there is no axis, one is created first.
The NaN values are not taken into account in the calculations for the box plot.
References:
McGill, R; Tukey, JW & Larsen, WA (1978) Variations of Box Plots. The American Statistician, Vol.32 No. 1, pp.12-16.
Kendall, MG & Stuart, A (1967): The Advanced Theory of Statistics, Vol.1, 2nd ed., Ch14., New York, Hafner Publishing Co.