patch
Creates 2D or 3D patches in an axis.
Syntax
h = patch(x, y, c)
h = patch(x, y, z, c)
h = patch('vertices', vertices_matrix, 'faces', faces_matrix)
h = patch(hAxes, ...)
Inputs
- x, y, z
- Coordinates of patch vertices.
- c
- Patch color.
- vertices_matrix
- An Mx2 or Mx3 matrix that contains the coordinates of the patch vertices. M is the number of vertices.
- faces_matrix
- An MxN matrix that contains the indices of the vertices of each patch. M is the number of patches and N is the number of vertices of each patch. NaN may be used if not all polygons have the same number of vertices (see the Examples section).
- hAxes
- Axis handle.
Outputs
- h
- Handle of the patch graphics object.
Examples
clf;
t1 = (1/16:1/8:1) * 2*pi;
t2 = ((1/16:1/8:1) + 1/32) * 2*pi;
x = tan (t1) - 0.8;
y = sin (t1);
h = patch (x',y','r')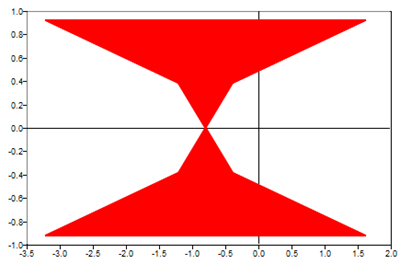
Figure 1. 2D patch plot example
x = [0 0.25 0.5 1 1 0.5 0.25 0 -0.5 -0.5]';
y = [0 0 0 0.5 1 1.5 1.5 1.5 1 0.5]';
verts = [x, y];
figure(1);
% Create one patch which constinst of 10 vertices
faces = [1:10];
h = patch('vertices',verts,'faces',faces);
figure(2);
% Create two patches each one consisting of 4 vertices
faces = [3 4 5 6; 8 9 10 1];
h = patch('vertices',verts,'faces',faces);
figure(3);
% Create two patches, the first patch consists of 6 vertices,
% the second patch consists of 4 vertices
faces = [2 3 4 5 6 7; 8 9 10 1 NaN NaN];
h = patch('vertices',verts,'faces',faces);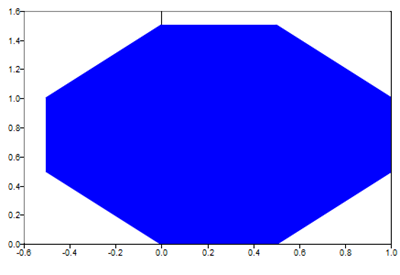
Figure 2. 2D patch plot defined by vertices and faces matrices
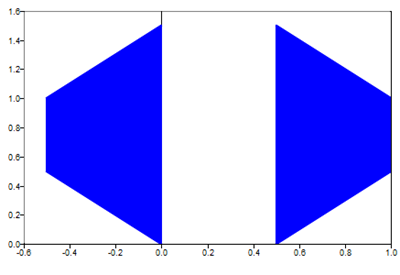
Figure 3. Create two-2D patches defined by vertices and faces matrices
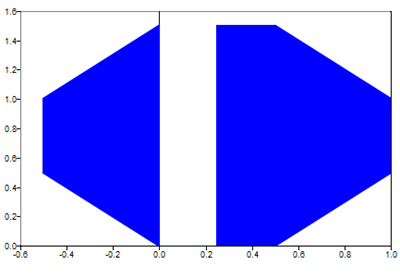
Figure 4. Create two-2D patches that have different number of vertices
clf;
x = [0 1 1 0; 1 1 0 0; 0.5 0.5 0.5 0.5];
y = [0 0 1 1; 0 1 1 0; 0.5 0.5 0.5 0.5];
z = [0 0 0 0; 0 0 0 0; 1 1 1 1];
h = patch(x,y,z,'r');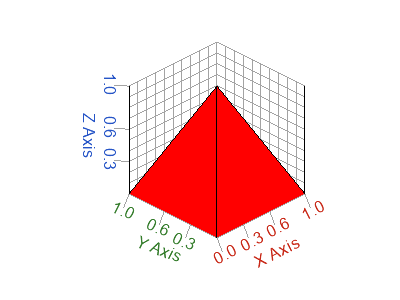
Figure 5. 3D patch plot example - triangles
clf;
x = [0 1 1 0; 1 1 0 0; 1 1 0 0; 0 1 1 0];
y = [0 0 1 1; 0 1 1 0; 0 1 1 0; 0 0 1 1];
z = [0 0 0 0; 0 0 0 0; 1 1 1 1; 1 1 1 1];
h = patch(x,y,z,'r');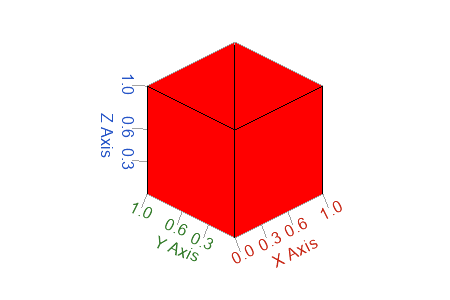
Figure 6. 3D patch plot example - quads
clf;
x = [0.5 0; 1.5 0; 2 0; 1.5, 0; 0.5 0; 0 0];
y = [0 0; 0 0.5; 0 1; 0 1.5; 0 1; 0 0.5];
z = [0 0.5; 0 0; 0.5 0; 1 0.5; 1 1; 0.5 1];
h = patch(x,y,z,'r');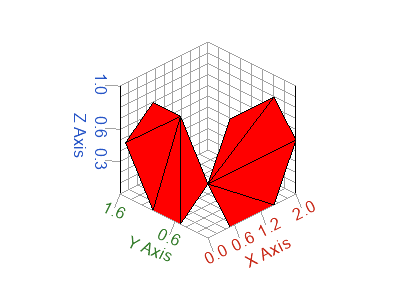
Figure 7. 3D patch plot example - polygons
clf;
verts = [0 2.5 0; 1 1.5 0; 1.5 1 0; 2 0.5 0; 2.5 0, 0.5; 2 0.5 1;
1.5, 1 1; 1 1.5 0.5; 1 1.5 1; 0 2.5 1; 0.5 2 0.5];
faces = [1 2 11 NaN NaN NaN; 9 10 11 NaN NaN NaN; 3 4 5 6 7 8];
h = patch('vertices',verts,'faces',faces);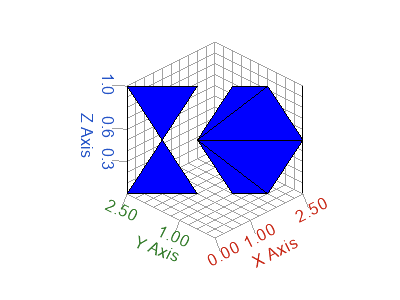
Figure 8. 3D patch plot defined by vertices and faces matrices
The color of a 3D patch can be defined as:
- one color for all faces of the patch
- a scalar per vertex mapped to the colormap
- a scalar per face mapped to the colormap
- a color per face
verts = [0 2.5 0; 1 1.5 0; 1.5 1 0; 2 0.5 0; 2.5 0, 0.5; 2 0.5 1;
1.5, 1 1; 1 1.5 0.5; 1 1.5 1; 0 2.5 1; 0.5 2 0.5];
faces = [1 2 11 NaN NaN NaN; 9 10 11 NaN NaN NaN; 3 4 5 6 7 8];
figure;
h = patch('vertices',verts,'faces',faces);
set(h,'facecolor',[250 0 250]]);

Figure 9. One color to all faces of the 3D patch
verts = [0 2.5 0; 1 1.5 0; 1.5 1 0; 2 0.5 0; 2.5 0, 0.5; 2 0.5 1;
1.5, 1 1; 1 1.5 0.5; 1 1.5 1; 0 2.5 1; 0.5 2 0.5];
faces = [1 2 11 NaN NaN NaN; 9 10 11 NaN NaN NaN; 3 4 5 6 7 8];
figure;
h = patch('vertices',verts,'faces',faces);
% facecolor = 'interp', the color of each face is defined by interpolating
% the cdata values of its vertices.
% if 'cdata' is not given then the 'zdata' values will be used.
set(h,'facecolor', 'interp');
figure;
h = patch('vertices',verts,'faces',faces);
% set a scalar value for each vertex
cdata = [0 1 2 NaN NaN NaN; 3 4 5 NaN NaN NaN; 6 7 8 9 10 11]';
set(h,'cdata', cdata)
set(h,'facecolor', 'interp')
figure;
h = patch('vertices',verts,'faces',faces);
% set a scalar value for each vertex
set(h,'cdata', cdata)
% facecolor = 'flat', the color of each face is defined by the cdata
% value of its first vertex.
set(h,'facecolor', 'flat')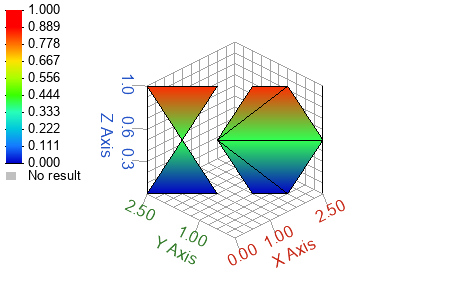
Figure 10. Patch color defined by the 'zdata' value of each vertex

Figure 11. Patch color defined by the 'cdata' value of each vertex

Figure 12. 'flat' facecolor
x = [0 1 1 0; 1 1 0 0; 1 1 0 0; 0 1 1 0];
y = [0 0 1 1; 0 1 1 0; 0 1 1 0; 0 0 1 1];
z = [0 0 0 0; 0 0 0 0; 1 1 1 1; 1 1 1 1];
figure;
h = patch(x,y,z,'r');
% set a scalar value for each face
set(h,'cdata',[0 9 6 4])
set(h,'facecolor', 'flat')
set(gca,'contourtype','discrete')
figure;
h = patch(x, y, z, 'r');
% set an rgb color for each face
cdata =[];
cdata(:,:,1) = [255 0 0 255]; % red component
cdata(:,:,2) = [0 0 255 0]; % green component
cdata(:,:,3) = [255 255 0 0]; % blue component
set(h,'cdata',cdata)
set(h,'facecolor', 'flat')
Figure 13. Patch color defined by a scalar value per face

Figure 14. RGB color per face
Comments
If there are no axes, they will be created first.