trisurf
Creates a 3D triangulated surface.
Syntax
h = trisurf(tri, x, y, z)
h = trisurf(tri, x, y, cdata)
h = trisurf(..., property, value, ...)
h = trisurf(hAxes, ...)
Inputs
- tri
- An Mx3 matrix, where M is the number of triangles. Each row contains the indices of a triangle in the x, y and z matrices. Usually, tri is the output of the delaunay function.
- x, y, z
- Coordinates of the vertices.
- cdata
- Color data for each vertex or triangle. cdata can be:
- a vector that contains a scalar value for each vertex
- a vector that contains a scalar value for each triangle
- an Mx3 matrix that contains an rgb color for each triangle
- property
- Properties that control the appearance or behavior of the graphics object.
- value
- Value of the properties.
- hAxes
- Axis handle.
Outputs
- h
- Handle of the trisurf graphics object.
Examples
[x, y] = meshgrid([0:0.2:2]);
z = sin(x)'*cos(y);
tri = delaunay (x(:), y(:));
figure;
h = trisurf(tri, x, y, z);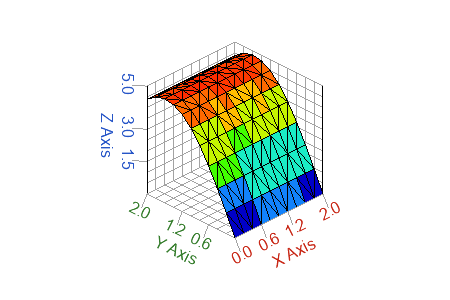
Figure 1. Simple trisurf example
[x, y] = meshgrid([0:0.4:2*pi]);
z=sin(x')*cos(x);
tri = delaunay (x(:), y(:));
figure;
h = trisurf(tri, x, y, z);
set(h,'facecolor','r')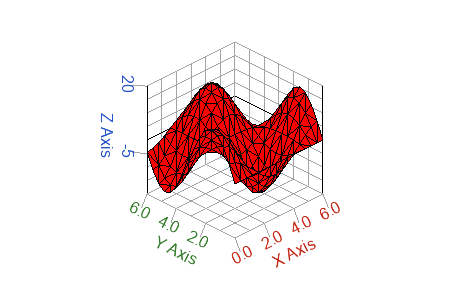
Figure 2. trisurf color
[x, y] = meshgrid([0:0.2:2]);
z = sin(x)'*cos(y);
tri = delaunay (x(:), y(:));
figure;
% cdata is a scalar per vertex
cdata = x(:);
h = trisurf(tri, x, y, z, cdata);
figure;
h = trisurf(tri, x, y, z, cdata);
% the triangle color is interpolated
set(h, 'facecolor','interp');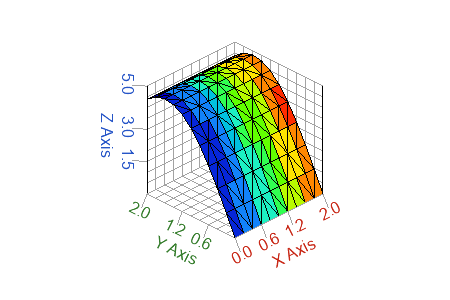
Figure 3. cdata per vertex
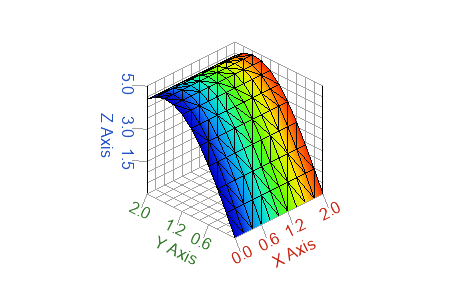
Figure 4. cdata per vertex, color is interpolated
[x, y] = meshgrid([0:0.5:2]);
z = cos(y)'*sin(x);
tri = delaunay (x(:), y(:));
figure;
% cdata is a scalar per triangle
cdata = 1:size(tri)(1);
h = trisurf(tri, x, y, z, cdata);
colormap(jet(12))
colorbar;
figure;
% cdata is an rgb color per triangle
cdata = plasma(size(tri)(1));
h = trisurf(tri, x, y, z, cdata);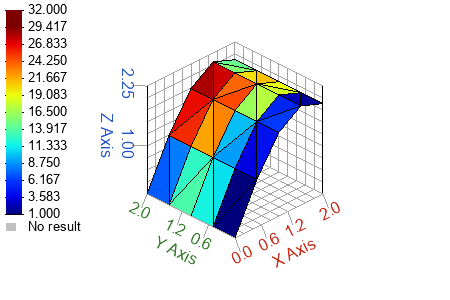
Figure 5. Scalar cdata per triangle
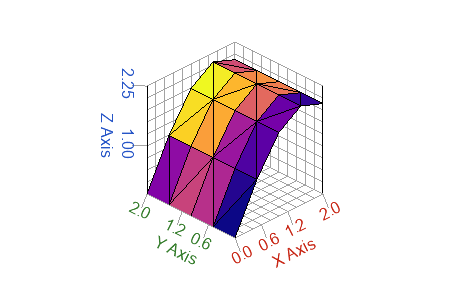
Figure 6. RGB color per triangle
Comments
If there are no axes, they will be created first.