Soft Soil Trackモデル
AltairのSoft Soil Trackモデルは、粘土質、乾燥砂、表土、氷で覆われた雪面などの圧縮可能なサーフェス上で履帯システムが示す動的な挙動をシミュレートする方法を提供します。
理論的な捉え方
現在のクローラ・履帯モデルでは、土の変形に応じて最終的に法線方向とせん断方向に応力が発生する場合、その変形は2つの独立した効果と見なされます。具体的には、法線方向(圧力と沈下量の関係)と接線方向(せん断応力とせん断変位量との関係)で土の強度が考慮されます。
圧力と沈下量の関係
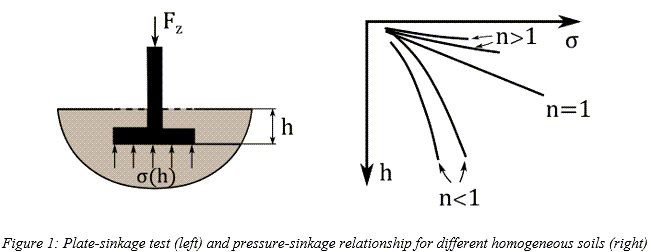
路面が均一であると仮定すると、その路面の圧力と沈下量の関係は図1に示した形態のいずれかとなり、Bekkerが提唱した次の経験式で特性記述できます。[1]
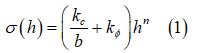
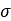 は圧力、
は圧力、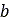 は矩形接触パッチ領域の幅、
は矩形接触パッチ領域の幅、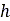 は沈下量、
は沈下量、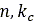 と
と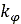 は圧力と沈下量に関連するパラメータです。
は圧力と沈下量に関連するパラメータです。
土の破壊
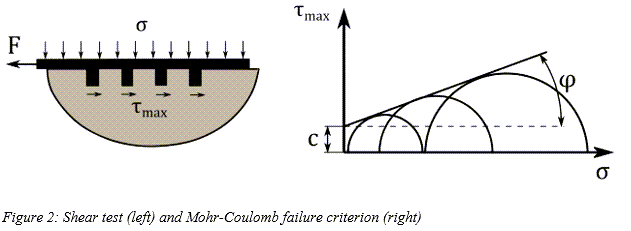
土の破壊に関してはさまざまな基準が提唱されています。幅広く使用されている基準の一つであるMohr-Coulomb基準では、土の最大せん断強度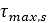 を次のように規定しています。
を次のように規定しています。
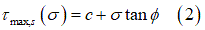
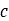 は見掛け凝集力、
は見掛け凝集力、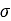 は法線方向応力、
は法線方向応力、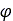 は材料の内部せん断抵抗が示す角度です。上記の各種パラメータは、図2に示すように、さまざまな圧力下でのせん断テストから導かれます。
は材料の内部せん断抵抗が示す角度です。上記の各種パラメータは、図2に示すように、さまざまな圧力下でのせん断テストから導かれます。
クローラ・履帯と路面との相互作用
接触ポイント
クローラ・履帯モデルでは、クローラ・履帯リンクの形状に応じて接触ポイントの数が1~5の範囲で変化します。具体的には、接触ポイントが1つの場合、クローラ・履帯リンク形状の記述には平坦な領域のみが使用されますが、接触ポイントが複数(2~5)の場合にはグローサーが追加されます。図3は、それぞれ接触ポイントが2つ、3つ、5つの、クローラ・履帯リンク形状の3つの例が示されています。

Normal Stress
Bekkerが提唱した圧力と沈下量の関係(式(1))を使用して、クローラ・履帯リンクの垂直応力は次のように求められます[2、3]
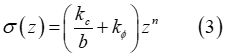
ここで、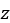 はクローラ・履帯リンクの沈下量ですが、パラメータbの定義はユーザーが指定します。特に、クローラ・履帯リンクの幅または最小寸法をこのパラメータの定義に使用できます。
はクローラ・履帯リンクの沈下量ですが、パラメータbの定義はユーザーが指定します。特に、クローラ・履帯リンクの幅または最小寸法をこのパラメータの定義に使用できます。
さらに、土による減衰の効果を考慮するために式(3)を修正できます[2-4]。その場合の法線方向応力は次のようになります。
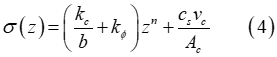
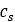 は土による減衰、
は土による減衰、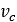 は速度あたりの土の圧縮率、
は速度あたりの土の圧縮率、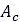 は接触パッチの面積です。
は接触パッチの面積です。
Shear Stress
せん断応力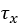 と
と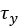 は、同じ式を使用して計算します[2-3]、[5]。
は、同じ式を使用して計算します[2-3]、[5]。
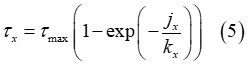
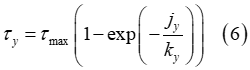
上記の式で、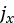 と
と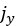 はそれぞれX方向とY方向のせん断変位量を示しています。さらに、
はそれぞれX方向とY方向のせん断変位量を示しています。さらに、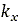 と
と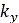 はせん断変形係数を表し、以下の式で求めることができます。
はせん断変形係数を表し、以下の式で求めることができます。
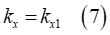
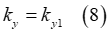
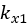 と
と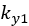 は定数項です。
は定数項です。
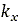 と
と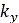 の一般的な値は、以下の刊行物で取り上げられています。
の一般的な値は、以下の刊行物で取り上げられています。- ‘Soil-tire interaction analysis for agricultural tractors: Modeling of traction performance and soil damage’ by A. Battiato, 2014 [6]
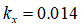 [m](粘土質の場合)
[m](粘土質の場合)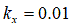 [m](粘土質ロームの場合)
[m](粘土質ロームの場合)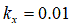 [m](シルト質ロームの場合)
[m](シルト質ロームの場合)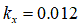 [m](ローム性砂の場合)
[m](ローム性砂の場合)
- ‘Terramechanics-based analysis for slope climbing capability of a lunar/planetary rover’ by K. Yoshida and G. Ishigami, 2004 [7]
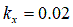 [m](乾燥砂の場合)
[m](乾燥砂の場合)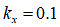 [m](レゴリス類似石の場合)
[m](レゴリス類似石の場合)
- ‘Analysis of off-road tire-soil interaction through analytical and finite element methods’ by H. Li, 2013 [4]
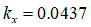 [m]
[m]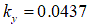 [m]
[m]
また、Wong[8]によると、収集した実験データに基づいて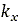 の値は、堅い砂地の0.01[m]から、ばら砂の0.025[m]にまでわたり、最大限圧縮した粘土質では約0.006[m]に達します。降り積もったままの新雪の場合、
の値は、堅い砂地の0.01[m]から、ばら砂の0.025[m]にまでわたり、最大限圧縮した粘土質では約0.006[m]に達します。降り積もったままの新雪の場合、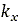 の値は0.025[m]から0.05[m]の範囲で変化します。
の値は0.025[m]から0.05[m]の範囲で変化します。
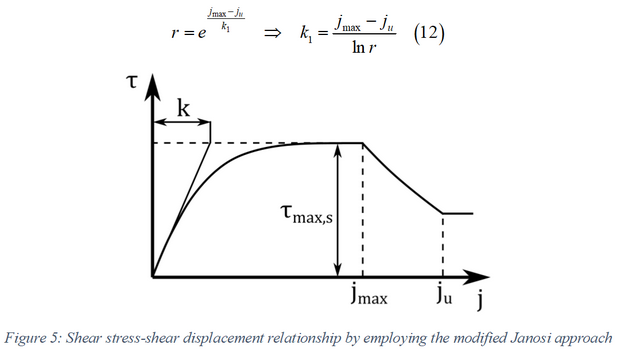
元のJanosiアプローチを使用して、式(2)で求めた土壌の最大せん断強度が、せん断応力の計算のために式(5)と(6)に代入され、以下の式になります。
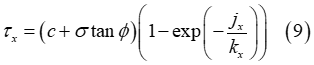
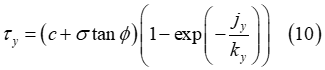
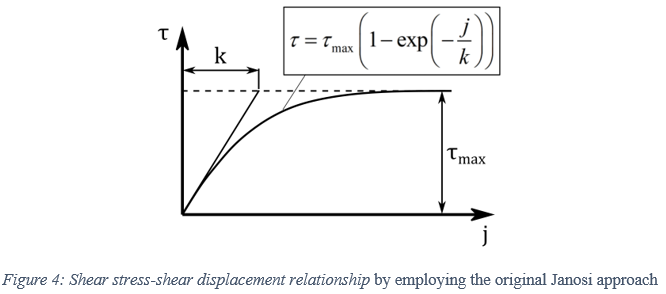
ただし、土壌破壊のため、せん断応力はせん断変位の特定の値以上に減少します[3]。ここで、この影響を考慮するための簡単なアプローチが提示されます。そこでは土壌の最大せん断強度がせん断変位の関数を構成します[3]。これに基づいて、改良型Janosiアプローチが次の形式で得られます。
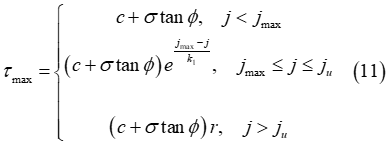
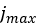 は土壌破壊の開始位置のせん断変位の値に対応し、
は土壌破壊の開始位置のせん断変位の値に対応し、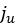 は限界せん断変位を表します。つまり、この値を上回るとせん断応力がせん断変位の影響を受けなくなります
は限界せん断変位を表します。つまり、この値を上回るとせん断応力がせん断変位の影響を受けなくなります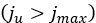 。さらに、パラメータrは最大せん断比を表します
。さらに、パラメータrは最大せん断比を表します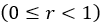 。
。
また、次の式は、式(11)で得られる最大せん断強度が次の連続関数に対応する状態を維持する必要があります。
グローサー効果
グローサー力の適切なモデリングはクローラ・履帯モデルに欠かせません。クローラ・履帯リンクの合計力に対する寄与が非常に大きいからです。土とグローサーの相互作用は土とブレードの相互作用と非常によく似ていることがわかっています。したがって、この相互作用の適切なモデリングには、McKyesが提唱したモデル[9]が適しています。この作業において、McKyesが提唱したモデル[9]は、一部の変更を含むグローサー力の計算に使用されます[3]。
マルチパス効果
- Normal Stress
-
マルチパス効果では、繰り返し法線荷重に対する土の応答を確定する必要があります。具体的には、土が事前圧縮されている場合は、法線方向応力の数学的記述を修正する必要があります。図6に示すように、初期の法線方向応力は弾性部分で構成されます
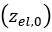 。この部分は、土壌とクローラ・履帯リンクの相互作用によってすでに作成されている弾性(無荷重)沈下量に等しくなります。続いて、圧力と沈下量との関係が式(3)に従って継続します。最終的に、無荷重弾性部分
。この部分は、土壌とクローラ・履帯リンクの相互作用によってすでに作成されている弾性(無荷重)沈下量に等しくなります。続いて、圧力と沈下量との関係が式(3)に従って継続します。最終的に、無荷重弾性部分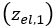 が発生します。
が発生します。土に誘引される変形の一部は弾性(弾性沈下)で、残りの部分(塑性沈下)は非可逆性です。この弾性部分は次の式で求めることができます
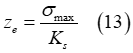
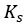 は土の弾性剛性です。
は土の弾性剛性です。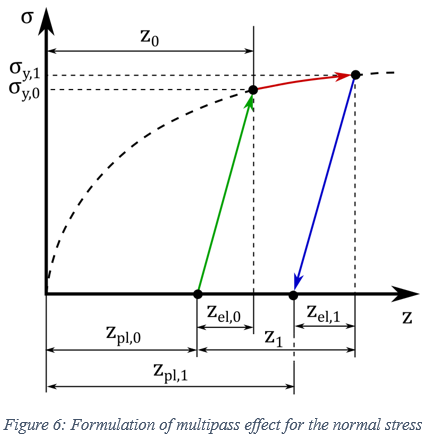
- Shear Stress
-
法線方向応力と同様のアプローチが、せん断応力のマルチパス効果の説明にも採用されます。具体的には、初期の土壌せん断応力は、次の式を使用してせん断変位の関数として定式化されます。
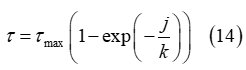
これは、せん断応力とせん断変位の特定の値(最大値)が導出されるまでです。その後、せん断関連のパラメータの最大値に基づいて、線形非荷重 / 荷重曲線が作成されます(図7を参照)。土壌の誘引された塑性せん断変位は次の式で求めることができます
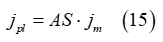
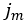 はせん断変位の(現在の)最大値で、ASは土壌のせん断塑性を示すユーザー定義のパラメータで構成されます
はせん断変位の(現在の)最大値で、ASは土壌のせん断塑性を示すユーザー定義のパラメータで構成されます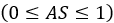 。特に、
。特に、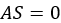 の場合は土壌の誘引されたせん断変位全体が弾性で、
の場合は土壌の誘引されたせん断変位全体が弾性で、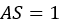 の場合はせん断変位が完全に塑性です。
の場合はせん断変位が完全に塑性です。見たところ、この線形カーブは、せん断変位の値の範囲が
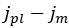 の場合の、せん断応力とせん断変位量の関係を示しています。それに対して、
の場合の、せん断応力とせん断変位量の関係を示しています。それに対して、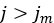 の場合、式(14)で得られる最初のカーブが再び使用されます。最後に、グローサー力のマルチパス効果の説明に対しても、同様のアプローチが採用されることに注意する必要があります。この場合はパラメータASの代わりにパラメータAMが使用されます[3]。
の場合、式(14)で得られる最初のカーブが再び使用されます。最後に、グローサー力のマルチパス効果の説明に対しても、同様のアプローチが採用されることに注意する必要があります。この場合はパラメータASの代わりにパラメータAMが使用されます[3]。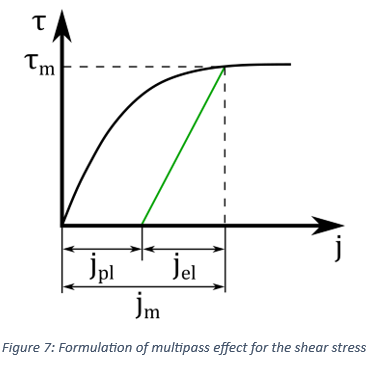
MotionSolveの出力要求
- 各リンクの参照マーカーを基準としたグローバル方向の土圧。
- 各リンクのリンクローカル座標での土の法線力。
- 各リンクの沈み込み、縦方向の滑り、横方向の滑り。
- 各ラップの総土圧。
- 全ラップの全リンクの総土圧。
出力要求のEntity setオプションを使用し、すべての接触に対する接触力の出力を要求できます。引張力や曲げ力などの力に対する出力はまたはそれぞれのジョイントや力において求めることができます。リンクの中間のマーカーは、力の参照マーカーとして使用できます。
参考資料
[1] M.G.Bekker, Introduction to terrain-vehicle systems. part i: The terrain. part ii: The vehicle.Michigan Univ Ann Arbor, 1969.
[2] D. Rubinstein and R. Hitron, “A detailed multi-body model for dynamic simulation of off-road tracked vehicles,” Journal of Terramechanics, 41(2-3), 163-173, 2004.
[3] D. Rubinstein and J. L. Coppock, “A detailed single-link track model for multi-body dynamic simulation of crawlers,” Journal of Terramechanics, 44(5), 355-364, 2007.
[4] Hao-Li, “Analysis of Off-Road Tire-Soil Interaction through Analytical and Finite Element Methods,” Technischen Universität Kaiserslautern, 2013.
[5] Z.Janosi, “The analytical determination of drawbar pull as a function of slip for tracked vehicles in deformable soils,” in Proc. of 1st Int. Conf. of ISTVS, 1961.
[6] A.Battiato, “Soil-tyre interaction analysis for agricultural tractors: modelling of traction performance and soil damage,” 2014.
[7] K. Yoshida, N. Mizuno, G. Ishigami, and A. Miwa, “Terramechanics-based analysis for slope climbing capability of a lunar/planetary rover,” in 24th Int. Symp. on Space Technology and Science, 2004.
[8] J.Y.Wong, Theory of ground vehicles.John Wiley & Sons, 2008.
[9] E.McKyes, Agricultural engineering soil mechanics. Elsevier, 2012.
[10] J.Y.Wong, Terramechanics and off-road vehicle engineering: terrain behaviour, off-road vehicle performance and design. Butterworth-heinemann, 2009.
[11] J.Y.Wong and A.R.Reece, “Prediction of rigid wheel performance based on the analysis of soil-wheel stresses Part I. Performance of driven rigid wheels,” J. Terramechanics, vol. 4, no. 1, pp. 81–98, 1967.
[12] I. Genya, M. Akiko, N. Keiji, and Y. Kazuya, “Terramechanics-Based Model for Steering Maneuver of Planetary Exploration Rovers on Loose Soil,” J. F. Robot., vol. 7, no. PART 1, pp. 81–86, 2015, doi: 10.1002/rob.