/ALE/GRID/LAPLACIAN

ブロックフォーマットキーワード 2D要素と3D要素を対象としてラプラス平滑化法を使用したALE節点の平滑化。

フォーマット

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
/ALE/GRID/LAPLACIAN
$λ$		`N`_iter

フィールド	内容	SI 単位の例
$λ$	節点更新のスケールファクター。 1 デフォルト = 1.0（実数）
`N`_iter	反復計算の回数。デフォルト = 1（整数）

次の式を使用して節点を平滑化します。(1)
$P_{i} \leftarrow P_{i} + λ Δ P_{i}$

ここで、 $λ \in [0, 1]$ はデフォルト値が1.00のユーザーパラメータです。(2)
$Δ P_{i} = \frac{1}{N_{c o n n e c t e d}} \sum_{j = 1}^{N_{c o n n e c t e d}} P_{j} - P_{i}$
複数回の反復計算を設定できますが、通常はサイクルあたり1回の反復計算で十分です（N_iter=1）。

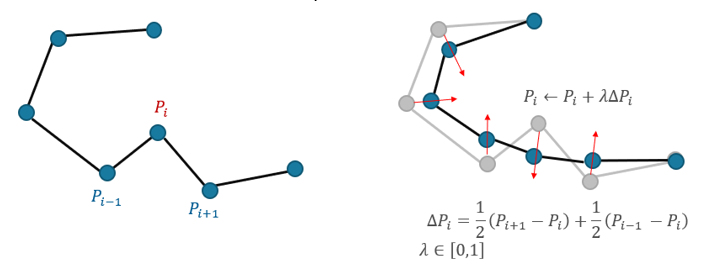
図 1.