ビーム要素（/PROP/BEAM, /PROP/INT_BEAM）

Radiossでは2種類のビーム要素が利用可能で、1次元構造とフレームに用いられます。これは軸力、せん断力、曲げ、およびねじりモーメントを伝達します（反対にトラスは軸力のみ支持します）。

古典的ビーム（/PROP/BEAM）

デフォルトの定式化はTimoshenko定式化に基づいているため、横せん断ひずみが考慮されます。この定式化は横せん断エネルギーを無視する通常のEuler-Bernoulli定式化に縮退させることができます。

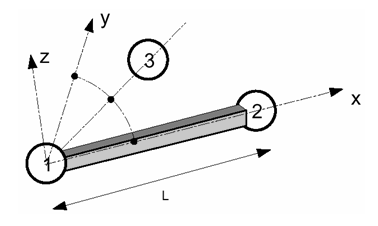
節点1と2が局所x-軸の定義に用いられます。局所y-軸はx-軸に直角で、t=0における節点1、2、3の平面内に置かれます。次に、平均のx-軸周りの回転を考慮して、それぞれのサイクルで位置は修正されます。局所 z-軸は右手則を用いて得られます。

Radiossではビーム形状はその断面面積と3つの断面積慣性モーメントで定義されます。局所 Y軸と Z軸に関する面積慣性モーメントは曲げのためで、次の式を用いて計算できます：(1)

$I_{y} = \iint_{A} z^{2} d y d z$

(2)

$I_{z} = \iint_{A} y^{2} d y d z$

局所X軸に関する面積慣性モーメントはねじりのためです。これは単純に、 $I_{y}$ と $I_{z}$ の和として得ることができます。ねじりモデルは中実断面で反りが無視できる場合のみ有効です。

ビーム要素の最小時間ステップは次の式を用いて決められます：(3)

$Δ t = \frac{a L}{c}$

ここで、

$c$: 音速; $\sqrt{E / ρ}$
$a = \frac{1}{2} \min (\sqrt{\min (4, 1 + \frac{b}{12})} \cdot F_{1}, \sqrt{\frac{b}{3}} \cdot F_{2})$
$F_{1} = \sqrt{1 + 2 d^{2}} - \sqrt{2} d$
$F_{2} = \min (F_{1}, \sqrt{1 + 2 d_{s}^{2}} - \sqrt{2} d_{s})$
$b = \frac{A L^{2}}{\max (I_{y}, I_{z})}$
$d = \max (d_{m}, d_{f})$
$d_{s} = d \cdot \max (1, \sqrt{\frac{12}{b}} \cdot \sqrt{1 + \frac{12 E}{\frac{5}{6} G b} (1 - I_{s h e a r})})$

ビーム断面を定義するユーザー入力パラメータは3つの面積慣性モーメントと断面積です。安定性と精度のために、次の制限を尊重することが推奨されます：(4)

$L > \sqrt{A}$

$0.01 A^{2} < I_{y} < 100 A^{2}$
$0.01 A^{2} < I_{z} < 100 A^{2}$
$0.1 (I_{y} + I_{z}) < I_{x} < 10 (I_{y} + I_{z})$

ビーム要素には材料則1と2のみ利用可能です。材料則2では、内力の関数にグローバル塑性モデルが使用されます。主要な仮定は、ビーム断面が中実で矩形であることです。断面と断面のモーメントの間の最適な関係は：

$12 I_{y} I_{z} = A^{4}$
$I_{x} = I_{y} + I_{z}$

このモデルは円形または楕円断面に対しても良い結果を与えます。薄肉断面に対しては、グローバル塑性モデルは誤った結果を与えるかもしれません。フレーム構造の1つのラインに対し1つのビーム要素を用いることは推奨しません。質量は節点に集中されます。そのため、正しい質量の分布を得るためには、細かいメッシュが必要です。これは特に動的効果が重要な場合には顕著になります。

加えて、 Radiossビーム要素では、モーメントがビームの長さ方向に変化しません。モーメントは一定であるという仮定の下でビームの中心で評価されます。応力も同様です。

その結果として、固定された単純梁では、モーメントがビームのつけ根ではなく中央で計算されるために、ビームに若干高い力を生みます。

注: ビーム要素の出力は局所座標系で表現されます。いくつかの結果において、それが平均X回転の考慮によって更新されるために、混乱を生じるかもしれません。例えば、ビームの1節点が完全に固定され、速度Vが他節点に与えられている場合、ビームはVの速度で回転しますが、局所座標系は速度V/2で回転します。これは、特にせん断力や曲げモーメントに間違った解釈を引き起こすかもしれません。

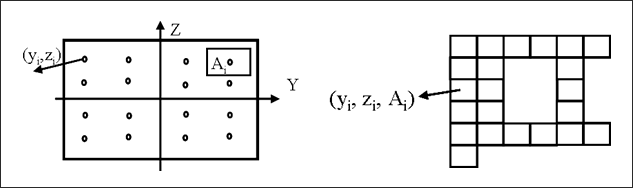
新しいビーム（/PROP/INT_BEAM）

要素の断面は100 までの積分点を用いて定義されます（図 2）。要素の断面特性、面積慣性モーメントと面積はRadiossによって次のように計算されます：(5)

$A = \sum A_{i} = \sum (d y_{i} d z_{i})$

(6)

$I_{z} = \sum A_{i} (y_{i}^{2} + \frac{1}{12} d y_{i}^{2})$

(7)

$I_{y} = \sum A_{i} (z_{i}^{2} + \frac{1}{12} d z_{i}^{2})$

ビームモデルは横せん断ひずみを考慮してねじりの反りはないTimoshenko理論に基づいています。深いビーム（短いビーム）の場合に用いることができます。断面積に複数の積分点を用いることで、それぞれの積分点で von Mises基準での弾塑性モデルを得ることを可能にし、古典的なビーム要素と異なり、断面は部分的に塑性化することができます（TYPE3）。材料則1と2に加えて、材料則36も用いることができます。しかしながら、要素は長さ方向には1積分点のみ持つため、フレーム構造の1つの線に1要素を用いることは、深さ方向だけでなく長さ方向の塑性の進展を考慮するために、推奨されません。

ビーム要素（/PROP/BEAM, /PROP/INT_BEAM）

古典的ビーム（/PROP/BEAM）

新しいビーム （/PROP/INT_BEAM）

新しいビーム（/PROP/INT_BEAM）