SS-V: 1180 Stress Concentration in a Filleted Notch

Figure 1.

The shaft is fixed at one end and a torque of 0.19625 lbf-in is applied on the other end. Shear stress is calculated as 1 psi using the following equation. The units are IPS.(1)

$${\tau }_0=Tc/J$$

Where,

$c$

$d/2$

$J$

$\pi d^4/32$

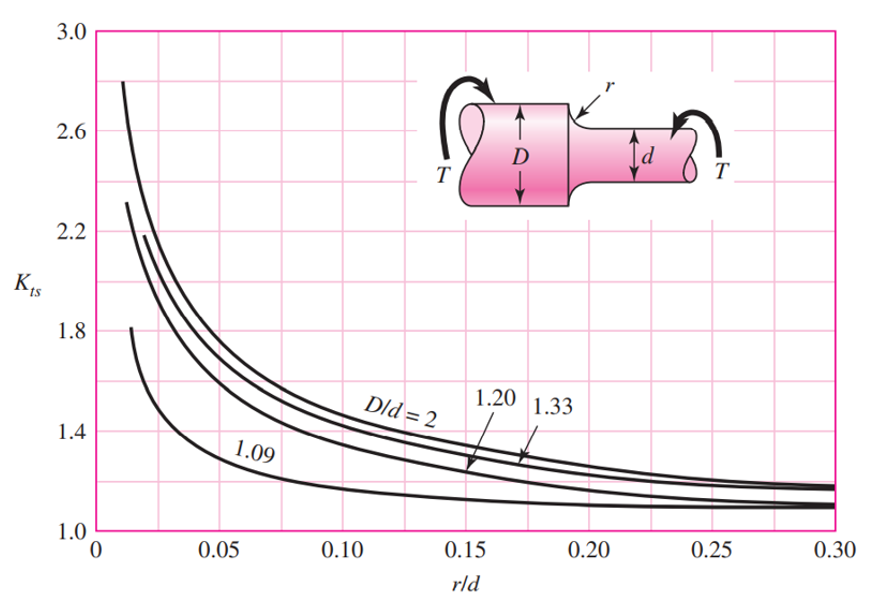
Model Dimensions

D = 2 in

d = 1 in

r = 0.05 in

r/d = 0.05

D/d = 2

• $\tau =K{\tau }_0$
• $K\sim 1.7$

The following table summarizes the stress results.