Tsai-Wu定式化を使用する直交異方性ソリッド材料を記述します。この材料は、Tsai-Wu基準を満たすまでは、3次元直交異方性弾性です。LAW12はLAW14を一般化および改善したものです。
弾性相
どちらの材料則も、弾性相で材料の直交異方性を記述するには、ヤング率、せん断係数、およびポアソン比(9パラメータ)が必要です。

図 1.
(1)
応力損傷

図 2.
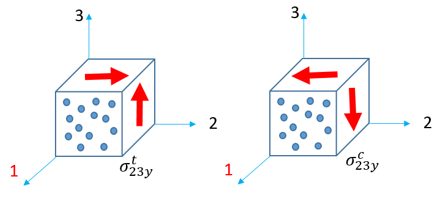
損傷では、応力制限
(引張り / 圧縮)が要求されます。これらの応力制限は、関連する3つの方向での引張り試験で確認することができます。
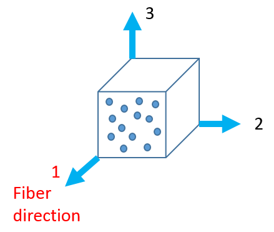
図 3.
応力制限に達すると、材料の損傷が始まります(応力は損傷パラメータ
により減少)。損傷(
)がD=1に達すると、応力は0になります。

図 4.
Tsai-Wu降伏基準
LAW12(3D_COMP)の場合、Tsai-Wu降伏基準は次のようになります:
(2)
Tsai-Wu基準の12の係数は、以下の試験による降伏応力を使用して決まります:
引張り / 圧縮試験
- 縦方向引張り / 圧縮(方向1):
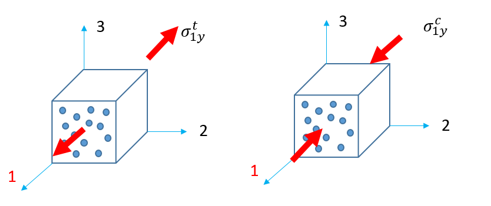
図 5.
(3)
(4)
- 横方向引張り / 圧縮(方向2):
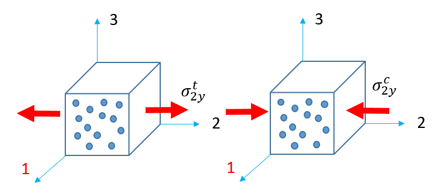
図 6.
(5)
(6)
- 横方向引張り / 圧縮(方向3):
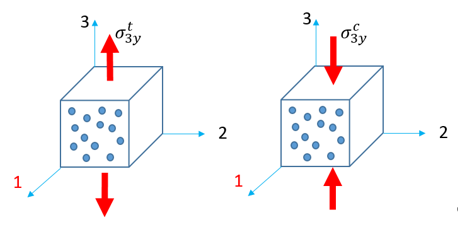
図 7.
(7)
(8)
これで、相互作用係数が次のように計算できます:
(9)
(10)
(11)
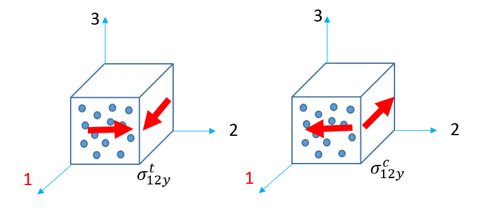
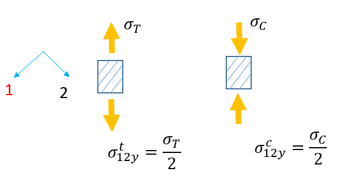
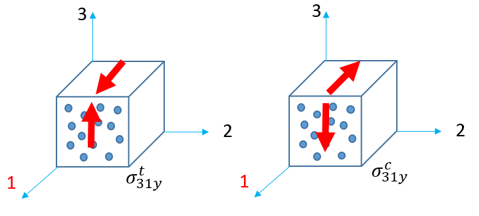
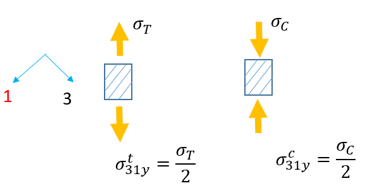
せん断試験
Tsai-Wu基準の計算には、
LAW12および
LAW14の以下に示すパラメータが要求されます:

図 13.
Tsai-Wuの降伏曲面は、
です。
である限り、材料は弾性相にあります。
になると降伏曲面を超え、材料は非線形相となります。
これら2つの材料則では、降伏曲面には次の係数も考慮する場合があります。
- 塑性仕事
とパラメータBおよびn
- ひずみ速度
とパラメータ
およびc (15)
これで、降伏曲面は
となります。
- 右記の場合、材料は弾性相になります;
- 右記の場合、材料は非線形相になります;
この降伏曲面
は、
(
)によって制限されます。ここで、
はTsai-Wu基準制限の最大値です。
パラメータ
B、
n、
cおよび
により、降伏曲面は1~
となります。
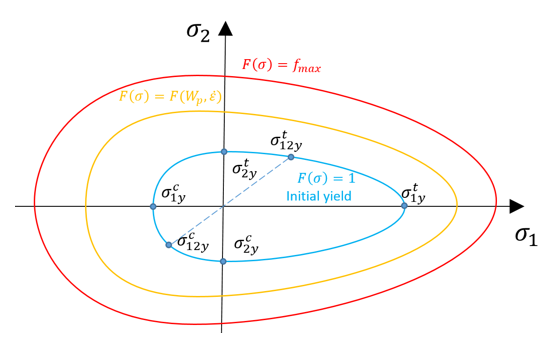
図 14. 1-2平面のTsai-Wu降伏基準