/MAT/LAW21 (DPRAG)
ブロックフォーマットキーワード この材料則は、Drucker-Prager降伏基準に基づくもので、岩石-コンクリートのように内部摩擦を伴う材料のモデル化に使用されます。これらの材料の塑性挙動は、材料内の圧力に依存します。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW21/mat_ID/unit_IDまたは/MAT/DPRAG/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| A0 | A1 | A2 | Amax | ||||||
| fct_IDf | Kt | FscaleP | |||||||
| Pext | |||||||||
| B | |||||||||
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| mat_ID | 材料識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子 (整数、最大10桁) |
|
| mat_title | 材料のタイトル (文字、最大100文字) |
|
| 初期密度 (実数) |
||
| E | ヤング率 (実数) |
|
| ポアソン比 (実数) |
||
| A0 | 材料塑性係数 (実数) |
|
| A1 | 材料塑性係数 (実数) |
|
| A2 | 材料塑性係数 (実数) |
|
| Amax | 制限的なフォンミーゼス応力。 デフォルトは1030に設定されます(実数) |
|
| fct_IDf |
を記述する関数識別子 (整数) |
|
| Kt | 引張体積弾性係数 3 (実数) |
|
| FscaleP | 圧力関数スケールファクター デフォルト = 1.0(実数) |
|
| 最小圧力 デフォルト = -1030(実数) |
||
| Pext | 外部圧力 4 デフォルト = 0(実数) |
|
| B | 除荷体積弾性係数 3 (実数) |
|
| 圧縮における最大体積ひずみ 5 (実数) |
例(Sand)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/DPRAG/1/1
Sand
# Init. dens.
1.6E-9
# E Nu
100 .3
# A0 A1 A2 Amax
1E-7 .001 1 0
# If Kt Fscale
2 1 0
# P_min
-1.5E-4
# B Mu_max
80 .4
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
Sand
# X Y
-1 0
0 0
.1 1000
.2 2500
.3 5000
.4 10000
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|コメント
- 流体力学的挙動はユーザー定義の関数
で定義されます。ここで、
- P
- 材料内の圧力
- 右記の式で示される体積ひずみ;
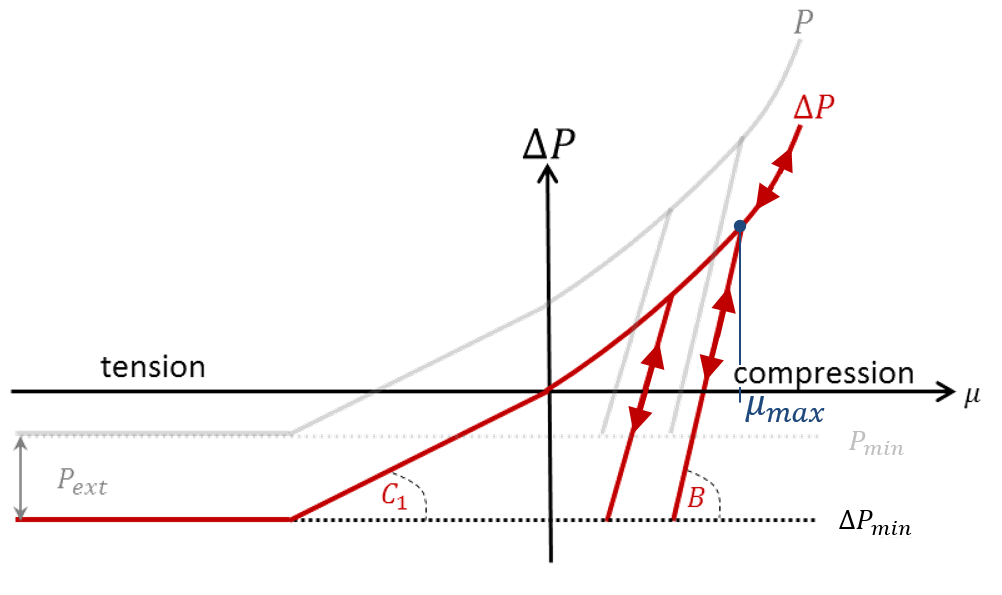
図 1. - Drucker-Prager降伏基準では、修正フォンミーゼス降伏基準を使用して塊状構造の圧力の影響を取り込みます:
(1) 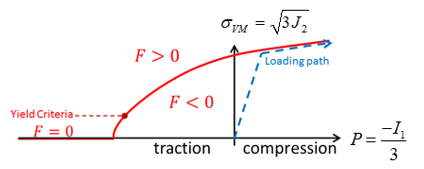
図 2.ここで、- 偏差応力の第2不変量で、
- P
- 圧力で、 で与えられる圧力( は第1応力不変量)
- A0、A1、およびA2
- 材料塑性係数
- 降伏基準はフォンミーゼス( )
- 除荷体積弾性率Bは を記述する関数の初期勾配に、引張体積弾性率Ktは除荷体積弾性率 Bの1/100に、Ktは正の値に、それぞれ設定することが推奨されます。
- 相対圧力定式化の場合は、外部圧力が必要です。この特定のケースでは、降伏基準とエネルギー統合に全圧力の値が必要とされます。Radiossは、
に相対する圧力を出力します。全圧力の値は以下から算出できます:
(2) 全圧力の限界は以下から算出できます:(3) の場合、出力結果が全圧力です:
および
- Bは除荷体積弾性率Bが定義されている場合、
における勾配
よりも大きくする必要があります。
- で の場合、除荷経路と荷重経路は同じです。
- または の場合、Bのデフォルト値は です。
- または の場合、 のデフォルト値は です。
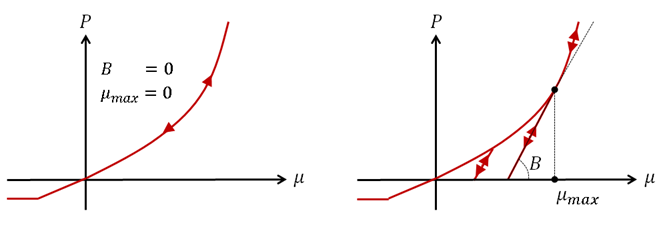
図 3.