/MAT/LAW75 (POROUS)
ブロックフォーマットキーワード P- 多孔質材料モデルを記述します。この材料はHerrmannモデルでの延性多孔質材料を記述します。これは8節点3次元ソリッド要素のみで機能し、ALEとは適合性がありません。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW75/mat_ID/unit_IDまたは/MAT/POROUS/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| mat_IDs | Iflag1 | Iflag2 | itemax | ||||||
| PE | Ps | n | |||||||
| tol | |||||||||
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| mat_ID | 材料識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子 (整数、最大10桁) |
|
| mat_title | 材料のタイトル (文字、最大100文字) |
|
| 多孔質材料の初期密度 (実数) |
||
| E | ヤング率 (実数) |
|
| ポアソン比 (実数) |
||
| mat_IDs | ソリッド(完全にコンパクトな)材料の材料識別子 (整数) |
|
| Iflag1 | 圧力定式化フラグ
(整数) |
|
| Iflag2 | 偏差応力定式化フラグ
(整数) |
|
| itemax | 計算の最大反復回数 デフォルト = 5(整数) |
|
| PE | 弾性コンパクト圧力 3 (実数) |
|
| Ps | ソリッド(マトリックス)コンパクト圧力 3 (実数) |
|
| n | 実験用データのフィッティングに使用する指数 3 デフォルト = 2(実数) |
|
| tol | 計算の収束判定基準
デフォルト = 10-8(実数) |
例(多孔質土壌)
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. LOCAL_UNIT_SYSTEm:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
g cm mus
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW75/1/1
porous soil
# RHO_I
1.7
# E NU
3 .3
# MAT_IDs IFLAG1 IFLAG2 ITEMAX
2 1 2 0
# PE PS N
.01 .05 0
# TOL
0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HYD_JCOOK/2/1
soil
# RHO_I RHO_O
1.76000004 0
# E nu
3.5999999 .300000012
# A B n epsmax sigmax
10000 0 0 0 0
# Pmin
0
# C EPS_DOT_0 M Tmelt Tmax
0 0 0 0 0
# RHOCP Troom
0 0
/EOS/POLYNOMIAL/2/1
EOS for soil
# C0 C1 C2 C3
0 2.81999993 2 -1.37
# C4 C5 E0 Psh RHO_0
1.53999996 1.53999996 0 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|コメント
- 空隙率
は次のように定義されます:
(1) ≥ 1 ( )である点にご留意ください。
ここで、- ソリッド(完全にコンパクトなマトリックス)材料の密度
- 多孔質材料の密度
- ソリッド(マトリックス)材料のEOSが次の場合:
(2) の場合、多孔質材料のEOSは次のようになります:- Herrmann定式の場合
- 修正Herrmann定式の場合
ここで( )は、単位初期体積あたりの内部エネルギーです。これは多孔質材料でもソリッド(マトリックス)材料でも同じです。
-
の場合、材料挙動は弾性で、
は塑性領域を記述します。
弾性領域では、圧力 による空隙率 の変化は可逆的です。
塑性領域での空隙率 は圧力に次のように依存すると仮定されます:(3) ここで、- 圧力が弾性コンパクト圧力に達する場所の空隙率
- 圧力はソリッド(マトリックス)コンパクト圧力に達します
- 初期空隙率
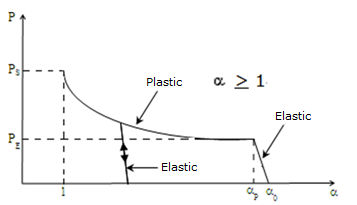
図 1.