CVT Model

使用されるシンボル:

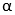= p、プライマリプーリー

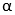= s、セカンダリプーリー

半径比 [状態]		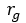プーリーの最小半径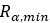
プーリーの慣性		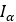プーリーの最大半径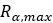
プーリーのトルク		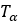プーリーの軸方向変位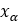
プーリーの実行半径		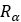最大トルク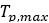
プーリーのRPM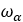
ベルトの質量		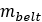軸からのフライウェイトの距離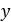
ベルトの長さ		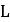フライウェイトの質量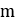
プーリーの距離		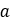ローラーの数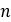
プーリーの半角		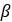プライマリプーリーのシーブ角度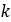
ラップ角		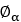プライマリシーブのランプ角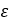
ねじれ角		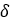内部スプリング剛性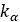
らせん半径		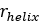内部スプリングのプリロード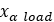
セカンダリスプリングの回転剛性		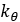回転スプリングのプリロード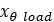
Static Friction Coefficient		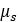Dynamic Friction Coefficient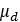

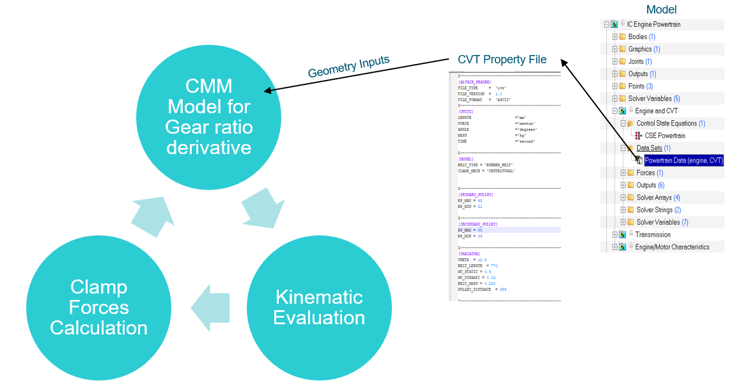CVTモデルの評価は次の手順で行われます:

図 1.

1.運動学的評価

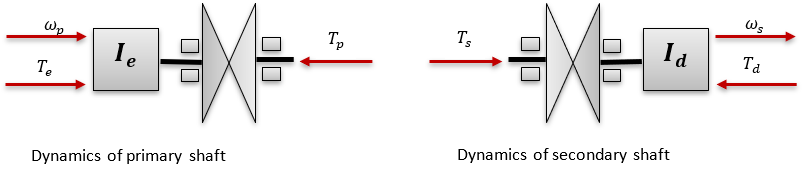
プライマリプーリーへの入力はエンジンPRMから行われ、次のように関連付けられます:

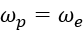
セカンダリプーリーの出力は変速機への入力となり、次のように関連付けられます:

CVTのシフト比は次の図のように可視化できます:

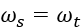
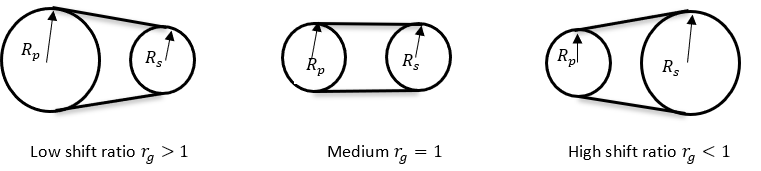図 2.

プーリーとバリエーターの半径比と形状情報があれば、プーリーの実行半径、ラップ角、軸方向変位はいつでも算出できます。バリエーターのベルトは剛体と見なされます。

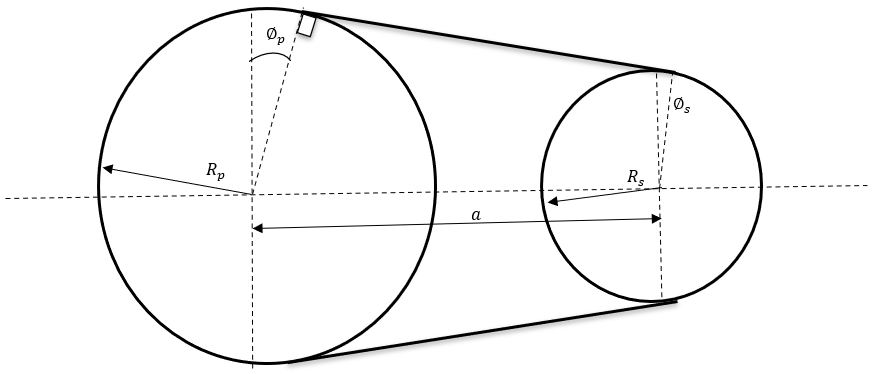図 3. バリエーターの形状設定

下の式はモデル内の幾何学的拘束を表すものです。簡略化すると、最終的な式が実行半径と角度に関して陰解法になっていることが確認できるため、Newton-Raphson法を使用して実行半径と角度を解析できます。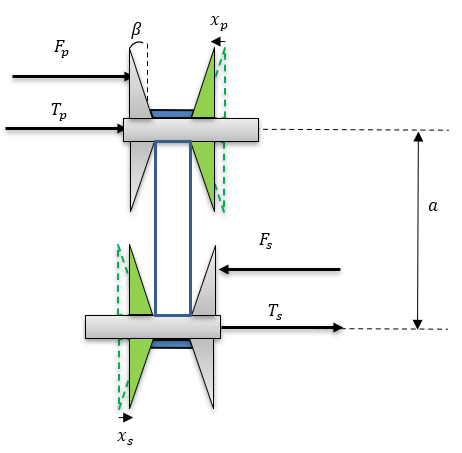

図 4. CVTのプーリーの軸上のシフト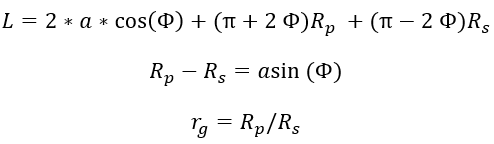

実行半径と角度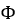を得た後、次のようにプーリーの軸方向変位とラップ角を計算できます。

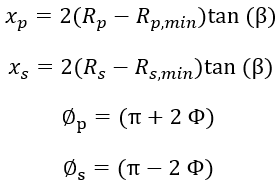
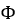下の図は、プーリーの半径、ラップ角およびの半径比を基準とした変化を示しています。

図 5.

2.計算用のクランプ

CVTモデルは、機械的、電動、油圧のCVTをモデル化できるように設定されます。デフォルトでは、MSはCVTプロパティファイル内の次のパラメータに基づいて機械的CVTをモデル化します。

CLAMP_MECHの値が‘CENTRIFUGAL’以外の場合、モデルに対してクランプ力の値をユーザーが入力する必要があります。クランプ力は、下の図に示すソルバー変数を使用してモデルに入力できます。

図 6.

プライマリプーリーのクランプ力:

‘CENTRIFUGAL’メカニズムは主にスクーターで使用されます。そこでは、エンジンシャフトの周囲をプライマリプーリーのシーブに沿って回転するフライウェイトを使用して、クランプ力が生成されます。このシーブには、フライウェイトによって生成された遠心力をクランプ力に変換するランププロファイルがあります。

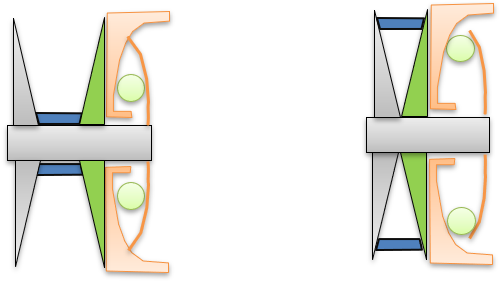図 7. ランプ上のローラーの重みのシフトメカニズム

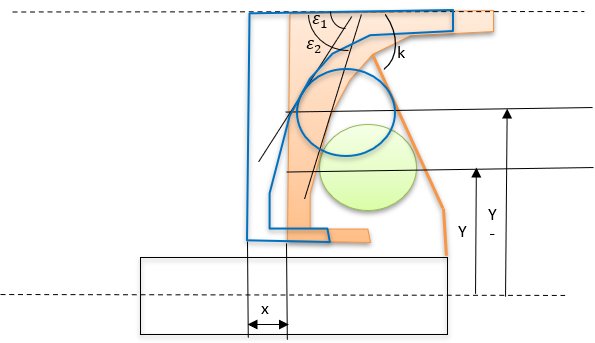図 8. ローラーとランプの形状

ランププロファイル:

下のカーブは、シャフト中心線からのローラーの距離（）とプライマリプーリーのシーブの軸上のシフト（）の関係を示しています。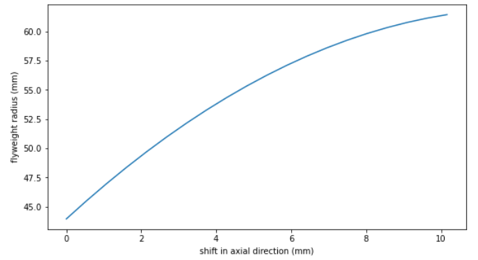

図 9.

下のカーブは、ランプ角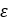（）とプライマリプーリーのシーブの軸上のシフト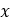（）の関係を示しています。

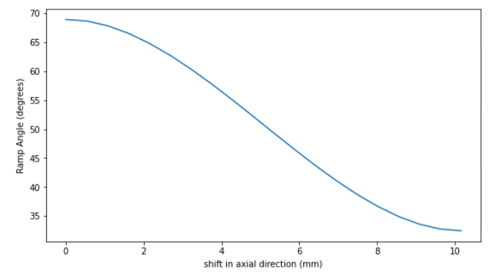図 10.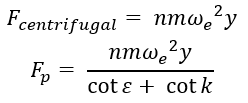

セカンダリプーリーのクランプ力:

セカンダリプーリーはトーションスプリングとトルクレギュレータカム（らせんカムとも呼ばれる）を使用して、クランプ力を生成します。

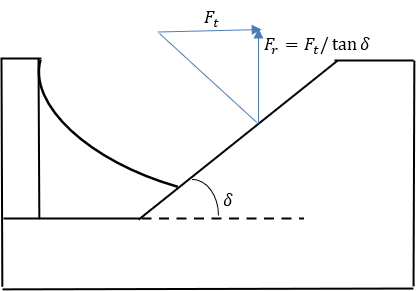図 11. らせんカム / トルクレギュレータの形状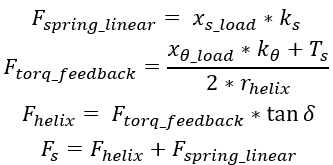

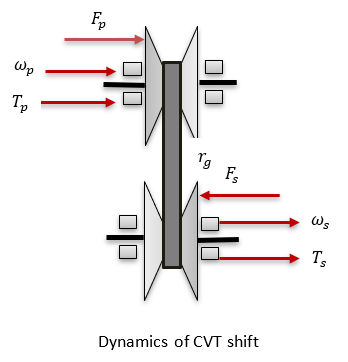
3.シフト比の計算

シフト比を計算するには、CMMモデルを使用します。CMMモデルに従って、プライマリプーリーとセカンダリプーリーのクランプ力比が静止クランプ力比と同じでない場合、バリエーターのベルトが移動します。静止クランプ力とは、ベルトが平衡を保ち移動することのないクランプ力の比です。

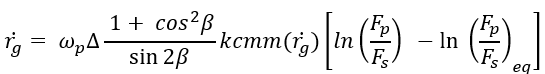
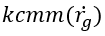係数は、実験的に測定される必要があります。

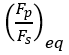は静止クランプ力比です。