/MAT/LAW117

ブロックフォーマットキーワードこの材料則は、法線方向と接線方向の2モードにおける延性接着材料の構成関係を表します。この材料則では、材料の弾性および破壊応答をモデル化します。

この材料は、ソリッド六面体要素（/BRICK）とTYPE43プロパティ（粘着ソリッド）のみに適合します。この材料は、破壊モデルとの適合性はありません。すべての損傷と破壊は、この材料内で直接定義されます。

フォーマット

(1)	(2)	(3)	(5)	(6)	(7)	(9)
/MAT/LAW117/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`EN`		`ET`	`I`_mass	`I`_del	`I`_rupt
`Fct_TN`	`Fct_TT`	`TN`	`TT`		`Fscale_x`
`GIC`		`GIIC`	`EXP_B`		`EXP_BK`	`Gamma`

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	（オプション）単位識別子（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度。（実数）	$[\frac{kg}{m^{3}}]$
`EN`	粘着要素の平面に対して垂直方向の剛性。（実数）	$[\frac{P a}{m}]$
`ET`	粘着要素の平面内の剛性。（実数）	$[\frac{P a}{m}]$
`I`_mass	質量計算フラグ = 1（デフォルト）要素質量は密度と平均面積を使用して計算されます。 = 2 要素質量は密度と体積を使用して計算される（整数）
`I`_del	要素を削除するための積分点の数を示す破壊フラグ（1～4）。デフォルト = 1（整数）
`I`_rupt	混合モードの変位則のフラグ。 = 1（デフォルト）べき乗則 = 2 Benzeggage-Kenane （実数）
`Fct_TN`	法線方向のピーク引張と要素メッシュサイズの関係を示す関数の識別子。（整数）
`Fct_TT`	接線方向のピーク引張と要素メッシュサイズの関係を示す関数の識別子。（整数）
`TN`	法線方向のピーク引張（デフォルト = 0）または`Fct_TN`の縦軸スケールファクター（デフォルト = 1）（実数）	$[Pa]$
`TT`	接線方向のピーク引張（デフォルト = 0）または`Fct_TT`の縦軸スケールファクター（デフォルト = 1）（実数）	$[Pa]$
`Fscale_x`	`Fct_TN`と`Fct_TT`の横軸スケールファクター。デフォルト = 1（実数）	$[m]$
`GIC`	モードIのエネルギー解放率。（実数）	$[Pa . m]$
`GIIC`	モードIIのエネルギー解放率。（実数）	$[Pa . m]$
`EXP_B`	混合モードのべき乗則指数。デフォルト = 2（実数）
`EXP_BK`	混合モードのBenzeggage-Kenane指数。（実数）
`Gamma`	Benzeggage-Kenane則のGamma指数。デフォルト = 1（実数）

例（結合材料）

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
Units
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW117/1/1
CONNECT MATERIAL
#              RHO_I
              7.8E-6
#                 EN                  ET     Imass      Idel     Irupt
                   5                 1.2         0         1         0
#   Fct_TN    Fct_TT                  TN                  TT            Fscale_x
         0         0                   2                 0.7                   0
#                GIC                GIIC               EXP_B              EXP_BK               Gamma
                   1                1.75                   2                   2                   1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

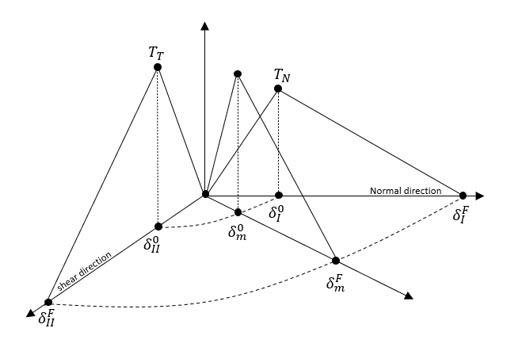
モードIは法線方向であり、モードIIはせん断方向です。 $δ_{I}$ は、 $δ_{z z}$ 方向に等しい法線方向の分離です。 $δ_{I I}$ は、接線方向の分離と等しくなります（ $δ_{I I} = \sqrt{δ_{y z} + δ_{z x}}$ ）。混合モードの変位は、 $δ_{m}$ と表されます。
モードIとモードIIの損傷開始変位は、それぞれ $δ_{I}^{0} = \frac{T_{N}}{E N}$ と $δ_{I I}^{0} = \frac{T_{T}}{E T}$ であり、混合モードでは次のとおりです：(1)
$δ_{m}^{0} = δ_{I}^{0} \cdot δ_{I I}^{0} \cdot \sqrt{\frac{1 + β^{2}}{{(δ_{I I}^{0})}^{2} + {(β \cdot δ_{I}^{0})}^{2}}}$

ここで、モード混合 $β = \frac{δ_{I I}}{δ_{I}}$ です。
破壊時の最大変位 $δ_{m}^{F}$ は、I_rupt=1の場合はべき乗則を使用して計算できます：(2)
$δ_{m}^{F} = \frac{2 (1 + β^{2})}{δ_{m}^{0}} \cdot {[{(\frac{E N}{G I C})}^{E X P_B} + {(\frac{β \cdot E T}{G I I C})}^{E X P_B}]}^{- (\frac{1}{E X P_B})}$

I_rupt =2の場合は、Benzeggage-Kenane則を使用して計算できます：(3)
$δ_{m}^{F} = \frac{2}{δ_{m}^{0} {(\frac{1}{1 + β^{2}} \cdot E N^{γ} + \frac{β^{2}}{1 + β^{2}} \cdot E T^{γ})}^{\frac{1}{γ}}} \cdot [G I C + (G I I C - G I C) {(\frac{β^{2} \cdot E T}{E N + β^{2} \cdot E T})}^{E X P_B K}]$
GICとGIICはそれぞれモードIとモードIIのピーク引張と最大変位の間のエネルギー解放率です。
$G I C = \frac{T N \cdot δ_{I}^{F}}{2}$ および $G I I C = \frac{T T \cdot δ_{I I}^{F}}{2}$

/MAT/LAW117

フォーマット

定義

例（結合材料）

コメント