| mat_ID |
材料識別子 (整数、最大10桁)
|
|
| unit_ID |
単位の識別子(オプション) (整数、最大10桁)
|
|
| mat_title |
材料のタイトル (文字、最大100文字)
|
|
|
ρi
|
初期密度。 (実数)
|
[kgm3]
|
|
EI
|
単位長さあたりの法線方向のヤング(剛性)率。 (実数)
|
[Pam]
|
|
EII
|
単位長さあたりの接線方向のせん断(剛性)係数。 デフォルト =
EII=EI
(実数)
|
[Pam]
|
| Thick |
基準粘着板厚。 (実数)
|
[m]
|
| Imass |
質量計算フラグ
- = 1(デフォルト)
- 要素質量は密度と平均面積を使用して計算されます。
(整数)
|
|
| Idel |
要素を削除するための積分点の数を示す破壊フラグ(1~4)。 デフォルト = 1(整数)
|
|
| Icrit |
降伏と損傷の開始フラグ。
(整数)
|
|
|
GCI_ini
|
モードI(法線方向)の初期臨界エネルギー解放率。 (実数)
|
[J]
|
|
GCI_inf
|
臨界エネルギー解放率の上限。GCI
のひずみ速度依存性を示します。 デフォルト = 0.0(実数)
|
[J]
|
|
˙εGI
|
GCひずみ速度依存性の参照(下限)ひずみ速度。
GCI_inf>0
の場合、定義する必要があります。
(実数)
|
[Hz]
|
|
fGI
|
モードIでの破壊前のエネルギー解放率の形状係数。 (実数)
|
|
|
GCII_ini
|
モードII(せん断)の初期臨界エネルギー解放率。 (実数)
|
[J]
|
|
GCII_inf
|
臨界エネルギー解放率の上限。GCII
のひずみ速度依存性を示します。 デフォルト = 0.0(実数)
|
[J]
|
|
˙εGII
|
GCひずみ速度依存性の参照(下限)ひずみ速度。
GCII_inf>0
の場合、定義する必要があります。
(実数)
|
[Hz]
|
|
fGII
|
モードIIでの破壊前のエネルギー解放率の形状係数。 (実数)
|
|
|
σA_I
|
モードIでの静的降伏応力。 (実数)
|
[Pa]
|
|
σB_I
|
モードIでのひずみ速度依存の降伏応力項。 (実数)
|
[Pa]
|
|
˙εI
|
モードIでの降伏応力速度依存性の参照(下限)ひずみ速度値。
σB_I>0
の場合、定義する必要があります。
(実数)
|
[Hz]
|
| Iorder_I |
モードIでのひずみ速度に対する降伏応力依存性の次数。
- = 1(デフォルト)
- ひずみ速度の線形対数依存性。
(整数)
|
|
| Ifail_I |
fGI
によって定義される破壊基準:
(整数)
|
|
|
σA_II
|
モードIIでの静的降伏応力。 (実数)
|
[Pa]
|
|
σB_II
|
モードIIでのひずみ速度依存の降伏応力項。 (実数)
|
[Pa]
|
|
˙εII
|
モードIIでの降伏応力速度依存性の参照(下限)ひずみ速度値。
σB_II>0
の場合、定義する必要があります。
(実数)
|
[Hz]
|
| Iorder_II |
モードIIでのひずみ速度の降伏応力依存性の次数。
- = 1(デフォルト)
- ひずみ速度の線形対数依存性。
(整数)
|
|
| Ifail_II |
fGII
によって定義される破壊基準:
(整数)
|
|
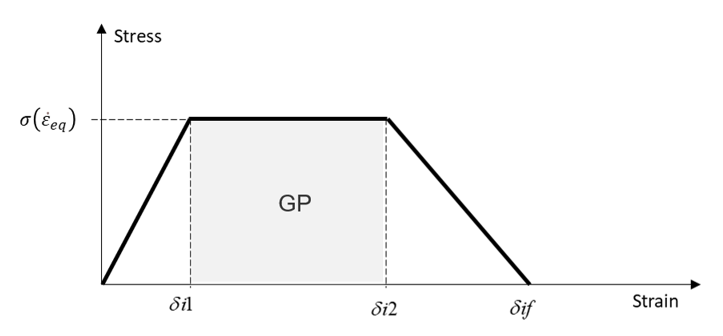 ここで、
ここで、