| prop_ID |
プロパティの識別子 (整数、最大10桁)
|
|
| unit_ID |
単位識別子 (整数、最大10桁)
|
|
| prop_title |
プロパティのタイトル (文字、最大100文字)
|
|
| Mass |
質量。
- Ileng = 0の場合
-
M
- Ileng = 1の場合
-
M⋅l0
(実数)
|
[kg]
または [kg⋅m]
|
| sens_ID |
センサーの識別子 (整数)
|
|
| Isflag |
センサーフラグ 4 5
- =2
- スプリング要素はアクティブまたは非アクティブ
(整数)
|
|
| Ileng |
単位長さあたりの入力フラグ
(整数)
|
|
| Fric |
Coulomb摩擦。 6 (実数)
|
|
| K1 |
剛性
K
、ただしIleng= 0
- fct_ID11= 0の場合
- 線形スプリングの剛性
- fct_ID11≠ 0の場合
- 非線形スプリングの除荷剛性
(実数)
|
[Ns]
|
剛性
Kl0
、ただしIleng= 1
- fct_ID11= 0の場合
- 線形スプリングの剛性
- fct_ID11≠ 0の場合
- 非線形スプリングの除荷剛性
(実数)
|
[Nm⋅s]
|
| C1 |
減衰
C
、ただしIleng= 0 (実数)
|
[Nsm]
|
| 減衰
Cl0
、ただしIleng= 1 (実数)
|
[Ns]
|
| A1 |
引張に対するひずみ速度の係数(力に対して均一) デフォルト = 1.0(実数)
|
[N]
|
| B1 |
引張に対するひずみ速度の対数係数(力に対して均一) (実数)
|
[N]
|
| D1 |
伸び速度のスケール係数 デフォルト = 1.0(実数)
|
[ms]
|
| fct_ID11 |
f(δ)
(Ileng= 0)または
f(ε)
(Ileng= 1)を定義する剛性関数識別子
(整数)
|
|
| H1 |
非線形スプリングの硬化フラグ
- = 2
- 引張における分離硬化を伴う非線形弾塑性スプリング
- = 6
- 等方硬化と非線形除荷を伴う非線形弾塑性スプリング
(整数)
|
|
| fct_ID21 |
g(˙δ)
(Ileng= 0)または
g(˙ε)
(Ileng=1)でのスプリング変位(または回転)速度に伴う力の変化を定義する関数 (整数)
|
|
| fct_ID31 |
除荷専用の関数 H1 = 4の場合:下方の降伏曲線を定義する関数識別子。
H1 = 5の場合:残差変位対最大変位を定義する関数識別子。
H1 = 6の場合:非線形除荷曲線を定義する関数識別子。
H1 = 7の場合:非線形除荷曲線を定義する関数識別子。
(整数)
|
|
| fct_ID41 |
h(˙δ)
(Ileng= 0)またはh(˙ε)
(Ileng=1)での速度または変形速度依存性を考慮する関数。 (整数)
|
|
|
δ1min
|
負の破壊変位(Ileng=0の場合)、または 負の破壊変位 x
l0
(Ileng=1の場合)
デフォルト = -1030(実数)
|
[m]
|
|
δ1max
|
正の破壊変位(Ileng=0の場合)、または 正の破壊変位 x
l0
(Ileng=1の場合)
デフォルト = 1030(実数)
|
[m]
|
| F1 |
δ
または
˙ε
のスケールファクター(
g(˙δ)
または
g(˙ε)
のfct_ID21関数の横軸) (実数)
|
[ms]
|
| E1 |
ひずみ速度効果(力に対して均一)であるg(˙δ)
またはg(˙ε)
(fct_ID21関数)のスケールファクター (実数)
|
[N]
|
| Ascale1 |
δ
または
ε
のスケールファクター(
f(δ)
または
f(ε)
のfct_ID11関数の横軸) (実数)
|
[m]
|
| Hscale1 |
力に対して均一な
h(˙δ)
または
h(˙ε)
(fct_ID41関数)のスケールファクター デフォルト = 1.0(実数)
|
|
| fct_IDfr |
プーリーの左右アーム間の力の差異の関数として摩擦係数Fricのスケーリングを定義する関数識別子 (整数)
|
|
| Ifr |
摩擦モデルフラグ 6
(整数)
|
|
| Yscale_F |
関数fct_IDfrの縦軸スケール デフォルト = 1.0(実数)
|
|
| Xscale_F |
関数fct_IDfrの横軸スケール デフォルト = 0.0(実数)
|
[N]
|
| F_min |
不可逆的摩擦モデルの負の制限力 Ifr = 1の場合のみ使用 6
デフォルト = -1030(実数)
|
[N]
|
| F_max |
不可逆的摩擦モデルの正の制限力 Ifr = 1の場合のみ使用 6
デフォルト = 1030(実数)
|
[N]
|
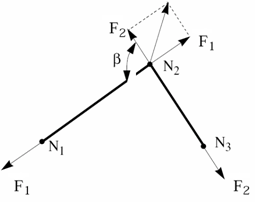
 節点1が節点2にスライドすると、プーリーを通して移動が不可能なノット(結び目)が節点1にあるかのように、ロッキングが起こります。図 2.
節点1が節点2にスライドすると、プーリーを通して移動が不可能なノット(結び目)が節点1にあるかのように、ロッキングが起こります。図 2.