/BEM/DAA

ブロックフォーマットキーワード流体の質量マトリックスが境界要素法で計算される水中爆発の二重漸近近似。

フォーマット

(1)	(2)	(3)	(5)	(6)	(7)	(8)	(9)
/BEM/DAA/`daa_ID`/`unit_ID`
`daa_title`
`surf_ID`	`grav_ID`
$ρ$ $ρ$		`C`	`P`_min
`X`_s		`Y`_s	`Z`_s
`I`_form	`Ipri`	`Ipres`		`Kform`	`Freesurf`	`Afterflow`	`Integr`

Ipres=1の場合挿入

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`P`_m		$θ$ $θ$		`a`		$a_{θ}$ $a_{θ}$

Ipres=2の場合挿入

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fct_ID`_P		`Fscale`_P

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`X`_c		`Y`_c		`Z`_c

grav_ID > 0またはFreesurf=2の場合挿入

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`X`_A		`Y`_A		`Z`_A
`Dir-X`		`Dir-Y`		`Dir-Z`

定義

フィールド	内容	SI 単位の例
`daa_ID`	DAAブロック識別子（整数、最大10桁）
`unit_ID`	単位識別子。（整数、最大10桁）
`daa_title`	DAAブロックタイトル（文字、最大100文字）
`surf_ID`	湿潤サーフェス識別子 2 3 （整数）
`grav_ID`	/GRAVオプション識別子（整数）
$ρ$ $ρ$	流体密度。（実数）	$[\frac{kg}{m^{3}}]$ $[\frac{kg}{m^{3}}]$
`C`	流体の音速（実数）	$[\frac{m}{s}]$ $[\frac{m}{s}]$
`P`_min	圧力のカットオフ( < 0 ) デフォルト = -10³⁰（実数）	$[Pa]$ $[Pa]$
`X`_s	スタンドオフポイントのX座標 3 （実数）	$[m]$ $[m]$
`Y`_s	スタンドオフポイントのY座標 3 （実数）	$[m]$ $[m]$
`Z`_s	スタンドオフポイントのZ座標 3 （実数）	$[m]$ $[m]$
`Iform`	BEMソリューションフラグ = 1（デフォルト）ガウス積分 = 2 解析的積分（整数）
`Ipri`	出力フラグレベル = 1（デフォルト）低減出力 = 2 フル出力（整数）
`Ipres`	圧力荷重フラグ 6 =1 圧力は、 $P_{i} (t) = P_{m} e^{- \frac{t}{θ}}$ $P_{i} (t) = P_{m} e^{- \frac{t}{θ}}$ として計算されます。 = 2 関数による入力（整数）
`Kform`	解析フラグ = 1（デフォルト） DAA1定式化 = 2 高周波数（整数）
`Freesurf`	自由サーフェスフラグ 6 = 1（デフォルト） × = 2 あり（整数）
`Afterflow`	アフターフローの計算 7 =1 × = 2（デフォルト）あり（整数）
`Integr`	時間整数フラグ =1 1次 = 2（デフォルト） 2次（整数）
`P`_m	最大圧力 5 （実数）	$[Pa]$ $[Pa]$
$θ$ $θ$	減衰時間（実数）	$[s]$ $[s]$
`a`	最大圧力定数 5 （実数）
$a_{θ}$ $a_{θ}$	圧力減衰時間定数 5 （実数）
`fct_ID`_P	入射圧力関数識別子（整数）
`Fscale`_P	`fct_ID`_Pの縦軸（圧力）のスケールファクター（実数）	$[Pa]$ $[Pa]$
`X`_C	装薬のX座標（実数）	$[m]$ $[m]$
`Y`_C	装薬のY座標（実数）	$[m]$ $[m]$
`Z`_C	装薬のZ座標（実数）	$[m]$ $[m]$
`X`_A	自由サーフェス上のポイントAのX座標（実数）	$[m]$ $[m]$
`Y`_A	自由サーフェス上のポイントAのY座標（実数）	$[m]$ $[m]$
`Z`_A	自由サーフェス上のポイントAのZ座標（実数）	$[m]$ $[m]$
`Dir-X`	自由サーフェス平面への法線のX座標（実数）
`Dir-Y`	自由サーフェス平面への法線のY座標（実数）
`Dir-Z`	自由サーフェス平面への法線のZ座標（実数）

構造全体がモデル化される必要があります。対称解析はサポートされません。
サーフェスの法線 $n$ $n$ は、流体に向いている必要があります。
(X_s, Y_s, Zs)で定義されたスタンドオフポイントは、入射圧力波が時間=0において与えられた位置です：

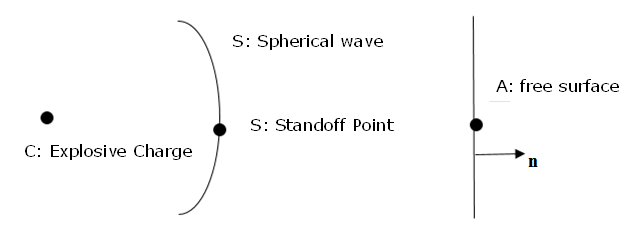
図 1.
平面波は球波を使用し、装薬を十分離して置いてシミュレートすることができます。

時間の関数としてのスタンドオフポイントにおける圧力は：(1)

P_{i} (t) = P_{m} e^{- \frac{t}{θ}}

$P_{i} (t) = P_{m} e^{- \frac{t}{θ}}$

ここで、

$P_{m}$ $P_{m}$: 最大圧力
$t$ $t$: 時間
$θ$ $θ$: 減衰時間

最大圧力と減衰時間は、以下を用いて計算できます：(2)

P_{m} = K {[\frac{W^{\frac{1}{3}}}{R}]}^{a}

$P_{m} = K {[\frac{W^{\frac{1}{3}}}{R}]}^{a}$

(3)

θ = K_{θ} W^{\frac{1}{3}} {[\frac{W^{\frac{1}{3}}}{R}]}_{θ}^{a_{θ}}

$θ = K_{θ} W^{\frac{1}{3}} {[\frac{W^{\frac{1}{3}}}{R}]}^{a_{θ}}$

$W$ $W$: 爆発物質量
$R$ $R$: 爆発までの距離
$K$ $K$ 、 $α$ $α$ 、 $K_{θ}$ $K_{θ}$ and $a_{θ}$ $a_{θ}$: 爆薬に依存する定数

W

$W$ （kg）、

R

$R$ （m）、

P_{m}

$P_{m}$ （MPaおよびms）の場合。

	$K$ $K$	$α$ $α$	$K_{θ}$ $K_{θ}$	$a_{θ}$ $a_{θ}$
TNT	52.12	1.180	0.0895	-0.185
PETN	56.21	1.194	0.0860	-0.257
HBX	53.51	1.144	0.0920	-0.247

自由サーフェスは、1つのポイントとその法線ベクトルによって定義される平面です。
アフターフロー法線速度は次のように計算されます：(4)
$v_{a f t e r f l o w} = \frac{cos γ}{ρ R} \int_{0}^{t} P (t) d t$ $v_{a f t e r f l o w} = \frac{\cos γ}{ρ R} \int_{0}^{t} P (t) d t$

P

流体ポイント

C

装薬ポイント

S

スタンドオフポイント

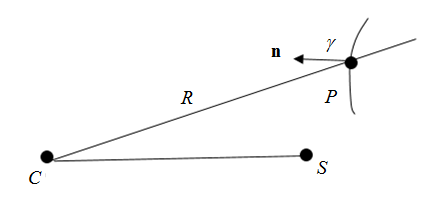
図 2.

Littlewood, J. de Runtz T. 2004."USA Code".Mecalog Workshop, Sophia Antipolis, France, 2004

Cole, Robert H. Underwater Explosion.Princeton University Press, 1948

/BEM/DAA

フォーマット

定義

コメント