/LOAD/PBLAST
ブロックフォーマットキーワード 構造上でエアブラストの圧力をシミュレートするシンプルな方法を提供します。
エアブラストの入射圧力は、実験データからフィッティングされ、爆風圧力はサーフェスの向きから爆発位置へ導かれます。ユーザーは、爆発位置、爆発時間および相当TNT質量を与える必要があります。
これは、到着時間と入射圧力が障害物について調整されないため、簡素化された載荷手法です。閉じ込め効果や地面効果は考慮されません。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /LOAD/PBLAST/load_ID/unit_ID | |||||||||
| load_title | |||||||||
| surf_ID | Exp_data | I_tshift | Ndt | IZ | Iform | Node_ID | |||
| xdet | Ydet | Zdet | Tdet | WTNT | |||||
| Pmin | Tstop | ||||||||
| Ground_ID | |||||||||
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| load_title | 荷重のタイトル (整数、最大10桁) |
|
| surf_ID | サーフェス識別子 (整数、最大10桁) |
|
| Exp_data | 実験データフラグ
(整数、最大10桁) |
|
| I_tshift | 時間シフトフラグ
(整数) |
|
| Ndt | 最小時間ステップのインターバルの数 Δtblast=inf(T0)NdtΔtblast=inf(T0)Ndt ここで、 T0T0 は正のフェイズの期間です。 デフォルト = 100(整数) |
|
| IZ | スケーリングされた距離の経時的な更新
(整数) |
|
| Iform | モデリングフラグ。
(整数) |
|
| Node_ID | 爆発位置を定義する節点識別子 定義されている場合、フラグXdet、YdetおよびZdetは無視されます。 |
|
| Xdet | 爆発位置のX座標 Node_ID ≠ 0の場合、無視されます。 デフォルト = 0.0(実数) |
[m][m] |
| Ydet | 爆発位置のY座標 Node_ID ≠ 0の場合、無視されます。 デフォルト = 0.0(実数) |
[m][m] |
| Zdet | 爆発位置のZ座標 Node_ID ≠ 0の場合、無視されます。 デフォルト = 0.0(実数) |
[m][m] |
| Tdet | 爆発時間 デフォルト = 0.0(実数) |
[s][s] |
| WTNT | 相当TNT質量 (実数) |
[Kg][Kg] |
| Pmin | 最小圧力 デフォルト = -1020(実数) |
[Pa][Pa] |
| Tstop | 停止時間 デフォルト = 1020(実数) |
[s][s] |
| Ground_ID | グラウンド定義のサーフェス識別子 Exp_data=1の場合、無視されます。 サーフェスタイプは/SURF/PLANEです。 デフォルト:原点=(0,0,0)、法線=(0,0,H) |
コメント
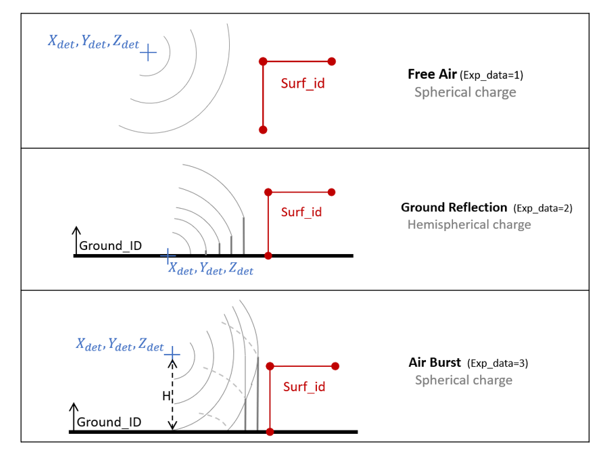
- モデリング状況はExp_dataフラグを使用して設定されます。ユーザーは、爆発データ(Xdet、Ydet、Zdet)、爆発質量(WTNT)、ターゲットサーフェス(surf_ID)、爆発時間(Tdet)を指定します。他のすべてのパラメータとフラグにはデフォルト値があります。Exp_data=3の場合は、爆発高さを定義する必要があります。図 1.
 ユーザーサーフェス上の指定されたポイントで、対応する半径 RR と爆発質量WTNTを使用して、衝風波動の特性値が決定されます(到着時間 tata 、最大圧力Pmax、正の期間 Δt+Δt+ 、衝撃 I+I+ など)。。入射波と反射波はどちらもFriedlanderの式に従います:
ユーザーサーフェス上の指定されたポイントで、対応する半径 RR と爆発質量WTNTを使用して、衝風波動の特性値が決定されます(到着時間 tata 、最大圧力Pmax、正の期間 Δt+Δt+ 、衝撃 I+I+ など)。。入射波と反射波はどちらもFriedlanderの式に従います:- Imodel = 1(Friedlanderモデル)の場合
(1) PFriedlander(t)=P⋅e−(t−ta)Δt+(1−t−taΔt+)PFriedlander(t)=P⋅e−(t−ta)Δt+(1−t−taΔt+) - If Imodel = 2(修正Friedlanderモデル)の場合
(2) PFriedlander(t)=Pmax⋅e−b(t−ta)Δt+(1−t−taΔt+)PFriedlander(t)=Pmax⋅e−b(t−ta)Δt+(1−t−taΔt+)
ここで、 Pmax,Δt+,taPmax,Δt+,ta は、スケーリングされた指定の距離 RW13RW1/3 において実験的にわかっています。 3
修正Friedlanderモデル(Imodel=2)では、‘b’は正のインパルスをフィッテングするために導入された減衰パラメータです。
'b’は次のように解かれます:(3) ta+Δt+∫taPFriedlander(t)dt=I+ta+Δt+∫taPFriedlander(t)dt=I+図 2. Friedlanderの式からの爆風プロファイル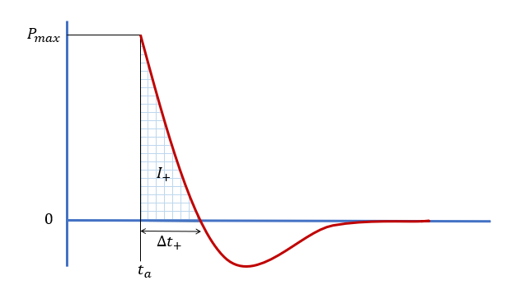
- Imodel = 1(Friedlanderモデル)の場合
- このフィッティングされた時刻歴関数
Pincident(t)Pincident(t)
および
Preflected(t)Preflected(t)
は、与えられたフェイスの重心Z’(図 3)における爆風の載荷
PBLAST(t)PBLAST(t)
の計算にも用いられます。 2
(4) PBLAST(t)={cos2θ⋅Preflected(t)+(1+cos θ−2cos2 θ)⋅Pincident(t) if cosθ>0 Pincident(t) if cosθ≤0PBLAST(t)={cos2θ⋅Preflected(t)+(1+cosθ−2cos2θ)⋅Pincident(t) if cosθ>0 Pincident(t) if cosθ≤0図 3. フェイスの重心Z’に付与される爆風圧力. フェイスの向きに依存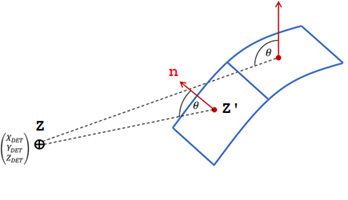
ここで、 θθ はサーフェスのセグメント(重心Z’)と爆発位置への方向との間の角度です。
これは、セグメントが直接爆発位置に面している場合、爆風圧力は反射圧力に等しく、セグメントが直接爆発位置に面していない場合は、入射圧力に等しいことを示しています。このモデル化は、到着時間と入射圧力が、関連する構造のシャドーイングで調整されていないため、簡易なものです。閉じ込め効果やトンネル効果も考慮されていません。
また、サーフェスが外を向いた法線ベクトルを有していることが必要とされます。
- Iz =1の場合、Rは一定で、Starter実行時にtime=0.00において計算されます。Iz =2の場合、 R=R(t)R=R(t) は、Engine計算時のサイクルごとに更新されます。
- WTNTが設定されていない場合、質量はゼロで、関連するサーフェスに圧力は付与されません。
- モデル化された爆発物がTNTではない場合、等価のTNT質量が与えられなければなりません。
- 実験データは単位系{cm, g, μsμs }を使用します。/BEGINで定義された単位は、実験データの単位をモデル単位に変換するために使用されます。したがって、/BEGINで定義された単位はモデルで使用される単位と精確に一致する必要があります。
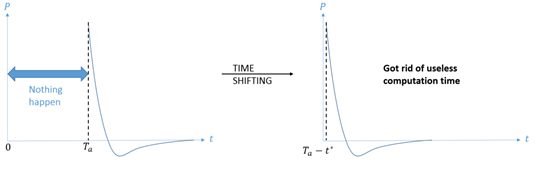
-
T=0T=0
から
t*=inf(Tarrival)t∗=inf(Tarrival)
までの計算時間をスキップすることが可能です。シフト値はStarter実行中に自動的に計算されます。
t*t∗
までの計算を無効にするには、I_tshiftの値を2にする必要があります。図 4. I_tshiftは最初の波の到着時間までの計算時間をスキップさせることが可能
-
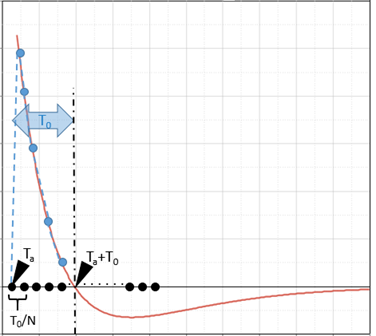
NdtNdt
パラメータは、構造の時間ステップが十分大きくない場合に最小時間ステップを課すことが可能です。
Δtblast=inf(T0)NdtΔtblast=inf(T0)Ndt
を課すと、正のフェイズ中、すなわち爆風波の指数関数的減少の間に十分な時間ステップが確保されます。デフォルトでは、
Ndt=100Ndt=100
です。図 5.
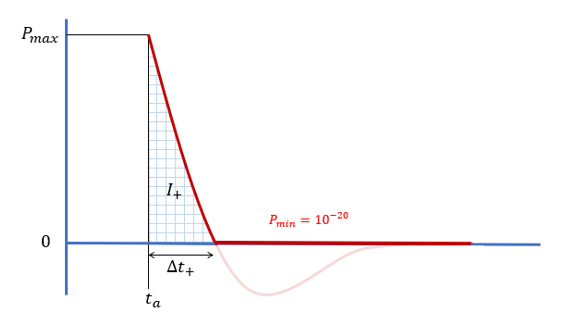
- Friedlander爆風モデルの正の部分を維持するために、パラメータ
PminPmin
が導入されました。
(5) P(t)=max(PBLAST(t),Pmin)P(t)=max(PBLAST(t),Pmin)図 6. 過剰圧力(載荷の正の部分)のみを維持するために使用されるパラメータ PminPmin