/BEM/FLOW
ブロックフォーマットキーワード 境界要素法による非圧縮性流体流れを記述します。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /BEM/FLOW/flow_ID/unit_ID | |||||||||
| flow_title | |||||||||
| surf_IDex | Nio | Iinside | fct_IDfsp | Fscalefsp | Ascalefsp | ||||
| grn_IDaux | Itest | Tole | |||||||
| Rho | Ivinf | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| surf_IDio | fct_IDnv | fct_IDp | Fscalenv | Fscalep | Ascalet | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Iform | Ipri | Dtflow | |||||||
| fct_IDv | Fscalev | Ascalev | |||||||
| Dirx | Diry | Dirz | |||||||
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| flow_ID | 非圧縮性流れブロックの識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子。 (整数、最大10桁) |
|
| flow_title | 非圧縮性流れブロックのタイトル (文字、最大100文字) |
|
| surf_IDex | 流れ外部サーフェスの識別子 (整数) |
|
| Nio | 流入-流出サーフェスの数 (整数) |
|
| Iinside | 内部流れまたは外部流れのフラグ
(整数) |
|
| fct_IDfsp | 停滞圧力曲線識別子 (整数) |
|
| Fscalefsp | 停滞圧力スケールファクター デフォルト = 1.0(実数) |
|
| Ascalefsp | 停滞圧力曲線の横軸スケールファクター デフォルト = 1.0(実数) |
|
| grn_IDaux | 補助節点グループ識別子 2 (整数) |
|
| Itest | テスト補助節点フラグ 2 (0より大きい整数) |
|
| Tole | 寸法公差 2 デフォルト = 1.e-5(実数) |
|
| Rho | 流体密度。 (実数) |
|
| Ivinf | 追加の速度フィールドフラグ 3 (0より大きい整数) |
|
| surf_IDio | 流入-流出サーフェス識別子 4 (整数) |
|
| fct_IDnv | 法線速度曲線 4 (整数) |
|
| fct_IDp | 作用圧力曲線 5 (整数) |
|
| Fscalenv | 法線速度スケールファクター デフォルト = 1.0(実数) |
|
| Fscalep | 作用圧力スケールファクター デフォルト = 1.0(実数) |
|
| Ascalet | 法線速度曲線と作用圧力曲線の横軸スケールファクター デフォルト = 1.0(実数) |
|
| Iform | 定式化フラグ 6
(整数 > 1) |
|
| Ipri | 出力レベル (1より大きい整数) |
|
| Dtflow | BEMマトリックスアセンブリの時間ステップ 7
(実数) |
|
| fct_IDv | 速度曲線の識別子。 (整数) |
|
| Fscalev | 速度のスケールファクター デフォルト = 1.0(実数) |
|
| Ascalev | 速度曲線の横軸スケールファクター デフォルト = 1.0(実数) |
|
| Dirx | 追加のフィールド方向ベクトルのX成分 (実数) |
|
| Diry | 追加のフィールド方向ベクトルのY成分 (実数) |
|
| Dirz | 追加のフィールド方向ベクトルのZ成分 (実数) |
例
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/BEM/FLOW/1
Flow 1
#surf_IDex Nio Iinside fct_IDfsp Fscale_fsp Ascale_fsp
3 2 1 0 0. 0.
#grn_IDaux Itest Tole
1 0 1e-5
# Rho Ivinf
1.0 0
#surf_IDio fct_IDnv fct_IDp Fscale_nv Fscale_p Ascale_t
2 1 0 10.0 0.0 1.0
#surf_IDio fct_IDnv fct_IDp Fscale_nv Fscale_p Ascale_t
1 0 1 0.0 101325.0 1.0
# Iform Ipri Dt_flow
1 1 1e-3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
Function 1
# X Y
0 1
100 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata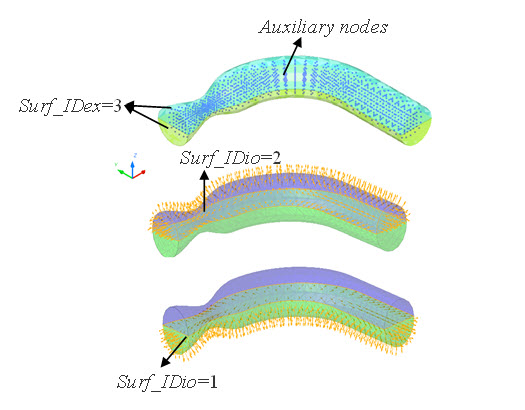
図 1.
コメント
- surf_IDexでは閉じたサーフェスを定義する必要があります。
- BEMを使用して、surf_IDexで定義されたサーフェスに属する節点について、流動電位、速度、および圧力が計算されます。
外観および後処理に関する懸念事項については、grn_IDauxに属する流れの内部にある一連の節点について流れ特性を計算できます。
Itest = 1の場合は、補助節点の実際の配置場所が内部(Iinside =1の場合)なのか外部(Iinside =2の場合)なのかにかかわらず、各時間ステップにおいてsurf_IDexで定義されたサーフェスがテストされます。その後、適切でない節点が現在の時間ステップについて取り消されます。
許容値Toleを使用して、閉じたサーフェス内のポイントのテストが実行されます。
- フラグIvinfが有効となるのは、surf_IDex(Iinside =2)で定義されたサーフェスの外部にある非有界領域内の流れ計算に対してのみです。
Ivinf = 1の場合は、流入条件は、自由空間内で定義された追加の均一流れによって定義されます。計算された流れは、surf_IDで定義されたサーフェスから無限距離にある追加の流れと等しくなります。
- Iinside = 0の場合:流れは、surf_IDexで定義されたサーフェスの内部で計算されます。法線速度が強制される1つ以上のサーフェスが存在する必要があるとともに、法線速度が自由なままになるサーフェスが1つのみ存在する必要があります。この自由サーフェスにおける速度は、surf_IDexで定義されたグローバルサーフェス上の流束のつり合いにより計算されます。
Iinside = 2およびIvinf = 0の場合: Iinside = 0、ただし、流れはsurf_IDexで定義されたサーフェスの外部で計算されます。
Iinside = 2かつIvinf = 1の場合: サーフェスの数は自由であり、これらすべてのサーフェス上で法線速度が強制される必要があります。
- 速度場からの圧力を減らすためには、流れ計算全体に対して1つの圧力のみを適用する必要があります。この圧力は、グローバル停滞圧力であっても、いずれかの流入-流出サーフェスにおける圧力であってもかまいません。
- コロケーション法は高速ですが、非常に複雑な形状を扱うのに十分なロバスト性を備えていない可能性があります。
Galerkin法はあらゆる状況に対応できますが、非常に低速です。
- BEMマトリックスは、サーフェスの形状のみに依存します。
Dtflow = 0(デフォルト)の場合は、BEMマトリックスはシミュレーションのすべてのサイクルでアセンブルされます(時間ステップは慣行的に有限要素の安定条件によって指定されます)。
Dtflow ≠ 0の場合は、max(Dtflow, Dt)を使用してBEMマトリックスが更新されます。ここで、Dtは有限要素の時間ステップです。