RD-E: 1600 Dummy Settling
Quasi-static loading analysis on a dummy, settling on a seat before crash analysis, using Altair Radioss explicit or Radioss implicit solvers.
- Standard explicit method with constant loading,
- Explicit method with kinetic relaxation (/KEREL)
- Explicit with dynamic relaxation (/DYREL)
- Explicit with dynamic relaxation with auto-defined adaptive damping (/ADYREL)
- Explicit with Rayleigh damping (/DAMP)
- Nonlinear implicit solution (/IMPL)
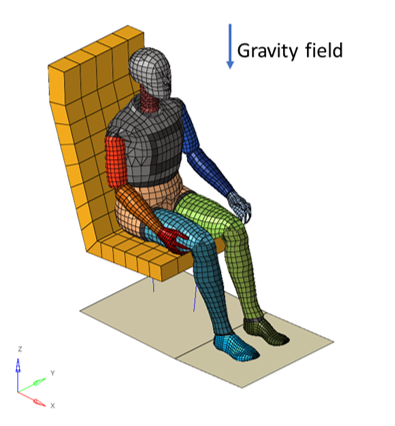
Figure 1. Problem studied
Options and Keywords Used
- /SHELL,/BRICK, and /BEAM elements
- Quasi-static analysis by explicit, kinetic and dynamic relaxation (/KEREL, /DYREL and /ADYREL), and Rayleigh damping (/DAMP)
- Contact interface (/INTER/TYPE7)
- Hyperfoam material (/MAT/LAW62 (VISC_HYP))
- Linear elastic material (/MAT/LAW1 (ELAST))
- General solid property set (/PROP/TYPE14 (SOLID)) and shell property (/PROP/TYPE1 (SHELL))
- Void material (/MAT/LAW0 (VOID)) and void property (/PROP/TYPE0 (VOID))
- Added mass (/ADMAS)
- Boundary conditions (/BCS)
- Gravity (/GRAV)
- Rigid body (/RBODY)
Input Files
- Explicit
- RD-E-1601_Explicit.zip
- Implicit
- RD-E-1602_Implicit.zip
Model Description
Model Method
- a dummy with only the external surface is defined as a rigid body
- a seat is comprised of six parts:
- foam seat back
- foam seat cushion
- seat back brace
- seat bottom brace
- seat legs
- the floor
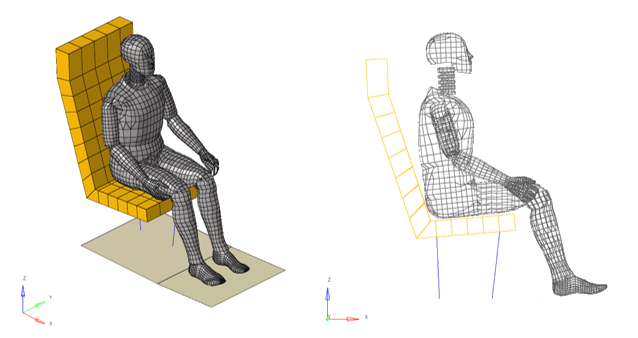
Figure 2. Model Mesh. Left: Perspective view - Shaded display; Right: Profile view - Edges display
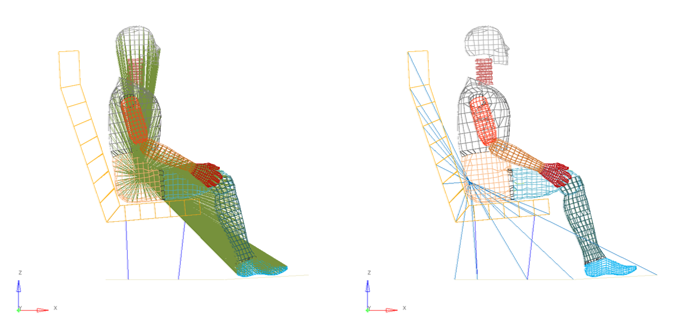
Figure 3. Rigid Bodies Setup
The seat structure and the floor are defined in a rigid body. Only the seat cushion parts are deformable during simulation.
The main node coordinates, and skew are extracted from the pelvis part of the dummy rigid body.
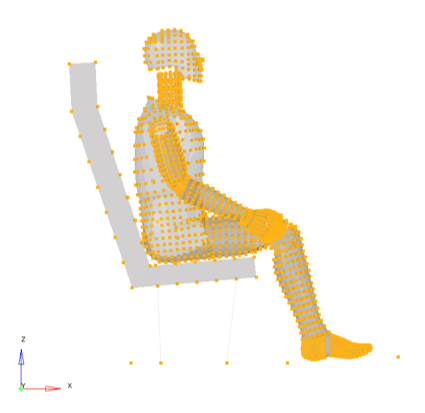
Figure 4. Input gravity function (-9810 mm/s-2) at selected nodes (yellow)
The main node of the seat and floor rigid body is clamped.
Figure 5. Boundary conditions on the rigid bodies’ main nodes
Material Properties
- Material Properties
- Value
- Young's modulus
- 210000
- Poisson's ratio
- 0.3
- Density
- 7.8E-9 ton/mm3
- Material Properties
- Value
- Ground shear modulus
- (0.02,2), (0.01,-2)
- Poisson's ratio (foam behavior)
- 0
- Density
- 7.8 x 10-9 ton/mm3
- Material Properties
- Value
- Young's modulus
- 2070
- Poisson's ratio
- 0.28
- Density
- 5E-11 ton/mm3
Element Properties
- Isolid
- 24 (HEPH)
- Icpre, Iframe and Ismstr
- Set to -1 (Recommended value)
The other parameters are set to default (0).
- Seat back thickness
- 2 mm
- Floor thickness
- 1 mm
Shell properties used are default value for all parameters (0).
- Area
- 2580 mm2
- Inertia
-
- IXX
- 554975 mm4
- IYY
- 554975 mm4
- IZZ
- 937908 mm4
- Dummy thickness
- 1 mm
Contact Interfaces
- Seat foams define the Main surface, Dummy parts define the Secondary nodes
- Dummy parts define the Main surface, Seat foams define the Secondary nodes (symmetrical contact)
- The floor defines the Main surface, dummy feet define the Secondary nodes
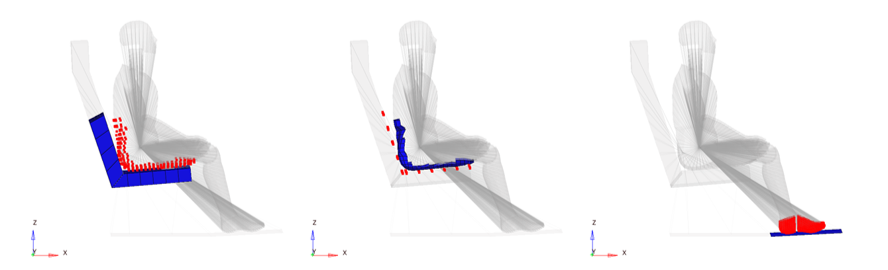
Figure 6. Contacts Modeling with TYPE7 Symmetrical Interface and foot-floor interface
- Contact gap
- 5 mm
- Coulomb friction
- 0.3
- Stiffness
- 4 (minimum stiffness between main and secondary)
- Minimum stiffness
- 1000 N/mm (usually value for automotive crash analysis)
- Friction formulation
- 2 (stiffness)
Refer to the Radioss Theory Manual and Starter Input for further information about the definition of the TYPE7 interface.
Resolution Methods
- Explicit solver:
A quasi-static simulation using a dynamic resolution method needs to minimize the dynamic effects to converge towards static equilibrium. This usually describes the pre-loading case prior to dynamic analysis. Thus, the quasi-static solution of gravity loading on the model is the steady-state part of the transient response.
A first analysis is done to view the dynamic effect due to gravity loading and compare the results with the different methods to reduce the dynamic effect.
To reduce the dynamic effect, the following options are available in the Engine file:- Kinetic energy relaxation (/KEREL)
All velocities are set to zero each time the kinetic energy reaches a maximum value (no additional input parameters are required).
- Dynamic relaxation (/DYREL)
- Dynamic relaxation with a user-defined damping factor and period to damp.
- The model without dynamic relaxation is computed to identify the period to damp and defined the parameters for the /DYREL card.
- Dynamic relaxation (/ADYREL)
- Dynamic relaxation with auto-defined adaptive damping.
- Radioss solver automatically defines the period to damp. There is no parameter to set.
- Rayleigh damping (/DAMP)
- Rayleigh mass and stiffness damping coefficients applied to a set of nodes for any nodal DOF either in local or global coordinate system.
- For this application, the mass needs to be damped to reduce the kinetic energy.
- The parameter, is defined as a damping percentage divided by the computation time step.
Detailed information about the different formulations are available in the Radioss Theory Manual.
- Kinetic energy relaxation (/KEREL)
- Implicit solver:
However, the implicit algorithm uses a global resolution which requires convergence for each time step and has low robustness in comparison to the explicit (null pivots, divergence for high nonlinearities, and so on).
The implicit methods result in solving a linear system for each time step, which is relatively expensive but enables a large time step: so there are few expensive calculations. The explicit method treats linear or nonlinear systems depending on the problem. It is less expensive and faster for each step, but requires short time steps to ensure stability of the scheme that has many inexpensive cycles.
For this example, the following implicit solution and solver is used:- Nonlinear solver
- Modified Newton method with relative residual in force (/IMPL/NONLIN/1)
- Linear solver
- Direct solver MUMPS (/IMPL/SOLVER/2)
- Quasi-static solution
- Considers the mass and inertia with a scale factor (/IMPL/QSTAT/DTSCAL)
- Time step
- Arc-length method is used to accelerate and to control the convergence (/IMPL/DT/2)
- Time step control
- Initial (/IMPL/DTINI), minimum and maximum time step (/IMPL/DT/STOP)
Detailed information about the different formulations are available in the Radioss Theory Manual.
Results
Curve and Animation
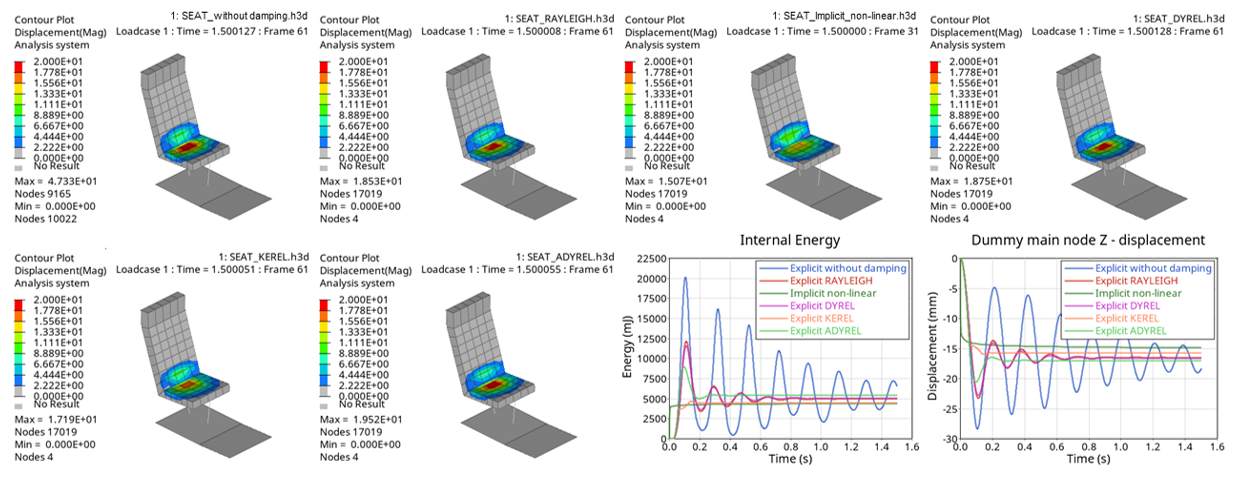
Figure 7. Results of displacement in Z-direction of the dummy and total internal energy
The results are similar for all methods used; except for the model without relaxation or damping (as is to be expected).
- Model
- Convergence time
- Explicit without damping
- Can not converge to static equilibrium
- Explicit ADYREL
- 0.4
- Explicit DYREL
- 1.5
- Explicit KEREL
- 0.2
- Explicit RAYLEIGH
- 1.5
- Implicit Nonlinear
- > 1.5
Conclusion
The model with dynamic relaxation (/DYREL), automatic dynamic relaxation (/ADYREL), and Rayleigh damping (/DAMP) converges to the same results. Automatic dynamic relaxation converges faster.
The results can be slightly different between the methods mainly because of the contact treatment, how the contact starts and how it evolves according to the elastic vibrations.