RD-E: 2700 Football (Soccer) Shots
Simulation of a soccer ball impact on a goal post.

Figure 1.
This is an example for demonstration purposes: During the Champions League final, 1976, between FC Bayern Munich and AS St. Etienne two shots of the French team rebounded off the opponent’s goal post. The fact that England was the only European country that has not replaced its goal posts with round poles has made French supporters believe that St. Etienne could have won the final if the goal posts had been replaced. Based on a simulation, an answer should be provided to these speculations. However, this controversy will undoubtedly continue.
Options and Keywords Used
- 4-node shell (Q4) and 3-node shell (T3), Fabric Law for Elastic Orthotropic Shells
- One-chambered airbag with hybrid input of injected gas (/MONVOL/AIRBAG1)
- Sensor (/SENSOR)
- Rigid wall (/RWALL) (Rigid cylinder and Rigid parallelogram)
- Rigid body (/RBODY)
- Initial velocity (/INIVEL)
- Rotational and translational velocity on a group of nodes in a given coordinate system (/INIVEL/AXIS)
- Translational material velocity (/INIVEL/TRA)
- Gravity load on a node group (/GRAV)
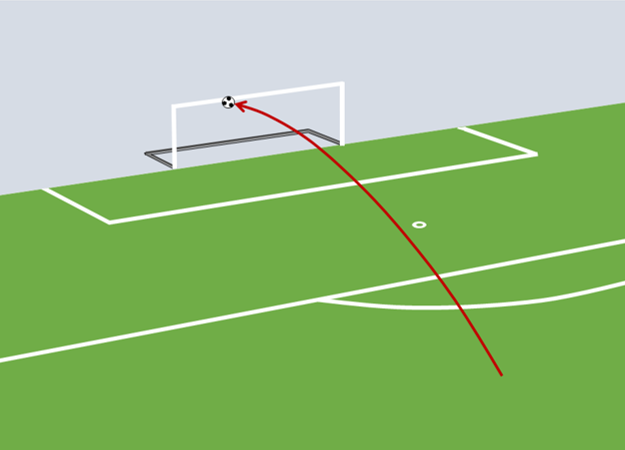
Figure 2. Trajectory of the Soccer Ball of Bathenay's Shot
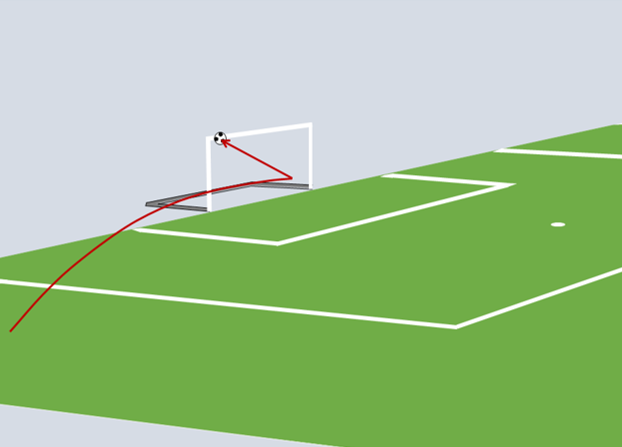
Figure 3. Trajectory of the Soccer Ball of Santini's Header
Input Files
Model Description
During the European football (Soccer) Cup final in 1976 (Bayern of Munich versus Saint Etienne), a shot from Bathenay and a header from Santini rebounded off the square cross-section frame of the German team's goal. The purpose of this demonstration is to determine the influence of a square or a round cross-section bar for both cases.
The main differences between both shots are the incidence, the velocity and the impact point of the ball on the bar (its vertical value).
- Initial density
- 2.01x10-3
- Young's modulus (dir. 1 and 2)
- 20000
- Shear modulus (12, 23 and 31)
- 10000
- Poisson ratio
- 0.29
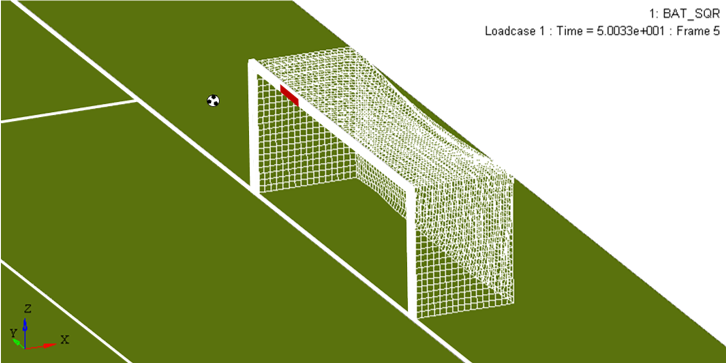
Figure 4. Geometry of the Problem
Model Method
Figure 5. Ball Mesh
Radioss Options Used
- A rigid body is created, containing all the nodes of the ball. It is deactivated just before impact on the bar.
- A rotational and translational initial velocities are applied to the rigid body’s main node using /INIVEL/AXIS. The velocities are defined in a local coordinate system using /FRAME/FIX.
- The goal posts are modeled with a cylindrical rigid wall for the round post and two rigid parallelograms for the square post.
- Gravity is taken into account using a gravity load.
- The ball is considered as an airbag, which is activated when the rigid body is deactivated.
Multiple Engine files are used. The second Engine file deactivates the ball rigid body using /RBODY/OFF. The time animation output is also increased to every 1 ms, so more details about the ball impacting the goal can be viewed. The third Engine file changes the animation output back to every 12.5 ms.
Results
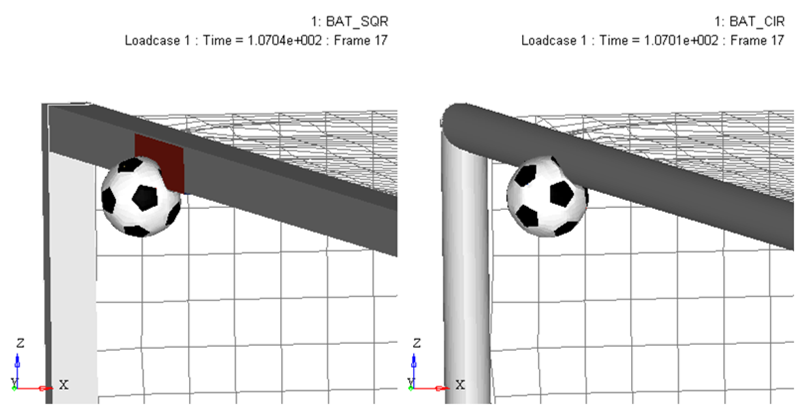
Figure 6. Impact of the Soccer Ball on a Square and a Round Cross-section
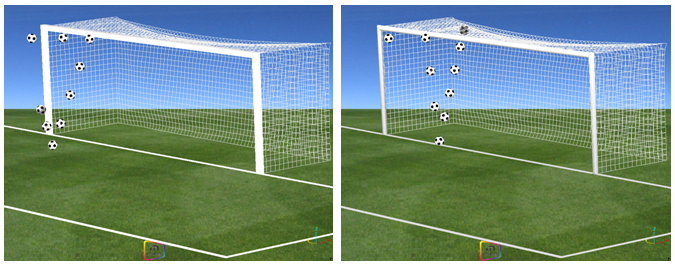
Figure 7. Trajectory of the Ball for Bathenay's Shot. (impact on a square and a round bar, respectively)
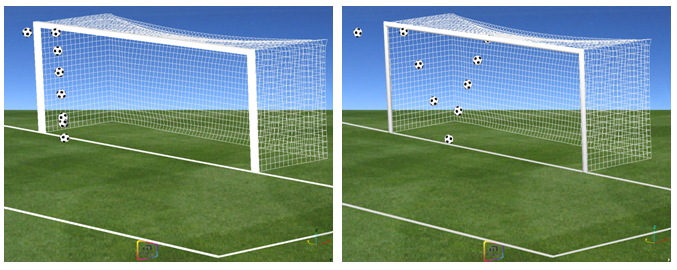
Figure 8. Trajectory of the Ball for Santini's Head. (impact on a square and a round bar, respectively)
Conclusion
Even using a simple modeling of the impact (bars modeled with rigid walls instead of parts), the simulation provides quite accurate results in the case of a square cross-section when simulations are compared to reality. The results obtained for the bars with a round cross-section show that the ball enters the goal for both shots. However, several impact parameters, such as friction and rotational velocity are estimated as calibrating the case of a square cross-section.