RD-E:0602 流体流れ
燃料タンクの転倒による流体流れのシミュレーション。リザーバータンクの転倒が水平に作用する重力を用いてモデル化されます。タンクのコンテナは変形しないものと仮定し、タンク内部の水と空気のみがALE定式化Iale=1を用いて考慮されます。
タンクが転倒する際の流体流れが検討されます。この例題はALE(Arbitrary Lagrangian Eulerian)定式化と流体力学2相材料則(/MAT/LAW37)が水と空気、タンク表面との間の相互作用のシミュレートに用いられます。タンクコンテナは変形しないと仮定され、モデル化されません。
使用されるオプションとキーワード
- 流体流れシミュレーションとALE定式化
- 3次元ソリッド要素
- 流体力学と2相液体-気体(/MAT/LAW37 (BIPHAS))
- ALE境界条件(/ALE/BCS)
- 重力(/GRAV)
- Iale=1を使用した、ALE特性定式化。
- 材料速度
- グリッド速度
境界内部の全ての節点はグリッドと材料速度がZ方向に固定され、右と左側面の節点は材料速度がXとZ方向に固定され、上と下の面の節点は材料速度がYとZ方向に固定されます。グリッド速度は境界で完全に固定され、材料速度が角で固定されます。
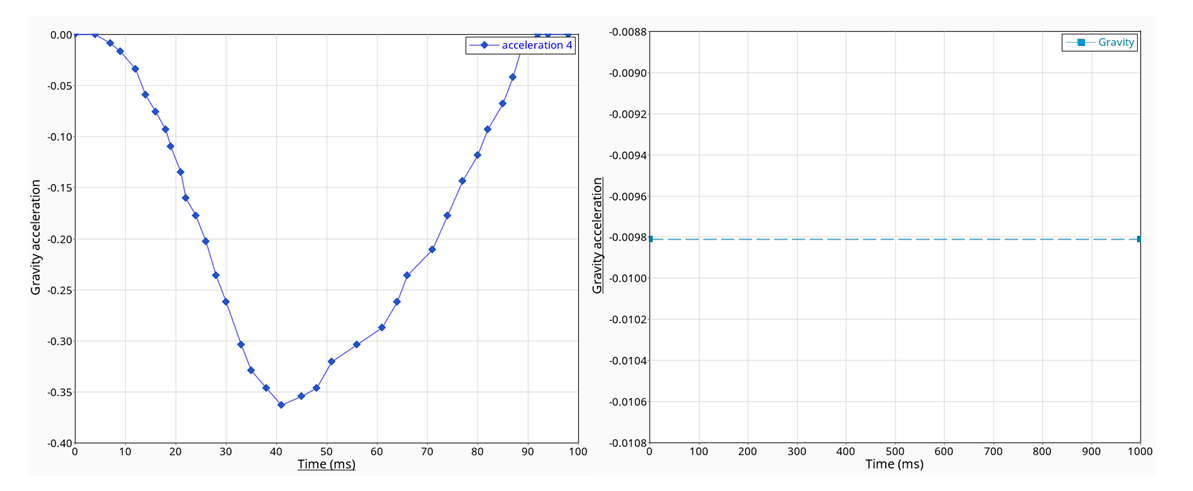
図 1. 左:可変加速度、右:重力
入力ファイル
モデル概要
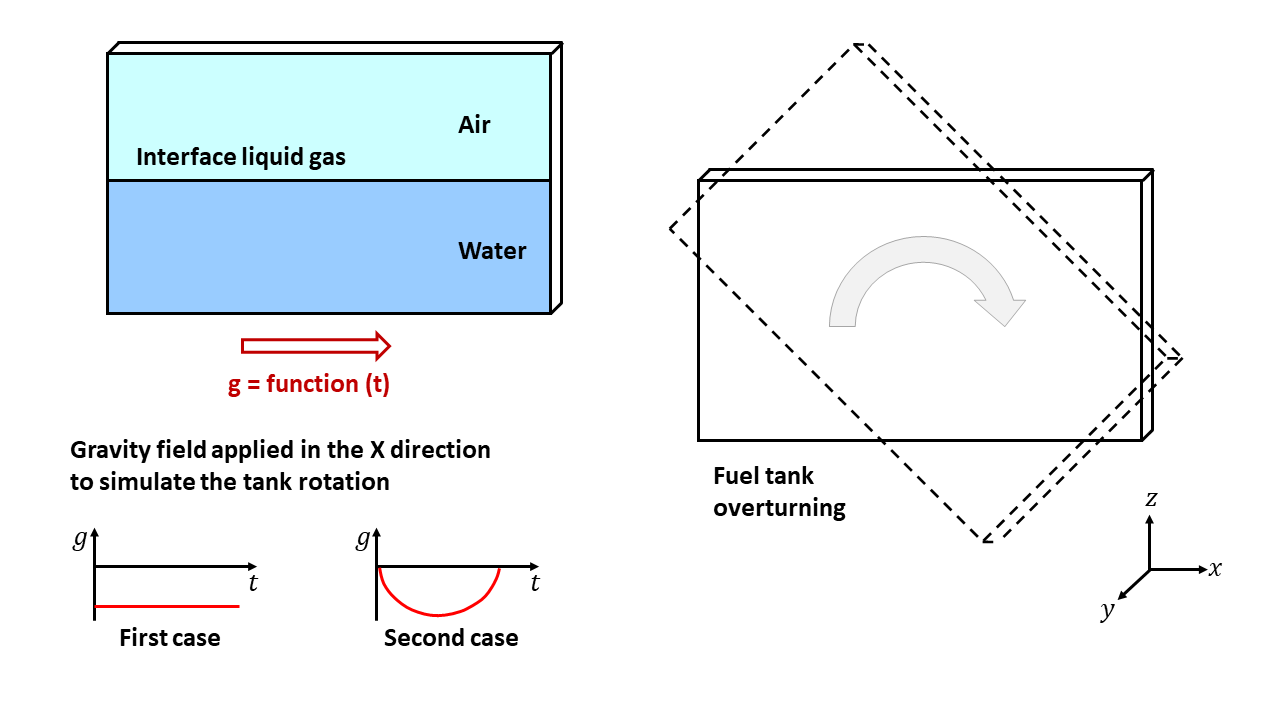
図 2. 問題の詳細
この例題では2つの荷重ケースを扱います: 燃料タンクの90度の瞬間的な回転(重力関数1)と漸進的な回転(重力関数2)です。
- 材料特性
- 値
- 空気密度
- 1.22x10-6
- 水の密度
- 0.001
- 気体の初期圧力
- 0.1
モデリング手法
2相材料、空気-水が流体力学材料則(/MAT/LAW37)で記述されます。完全な入力データを含むこの材料則の情報については前のセクションを参照してください。
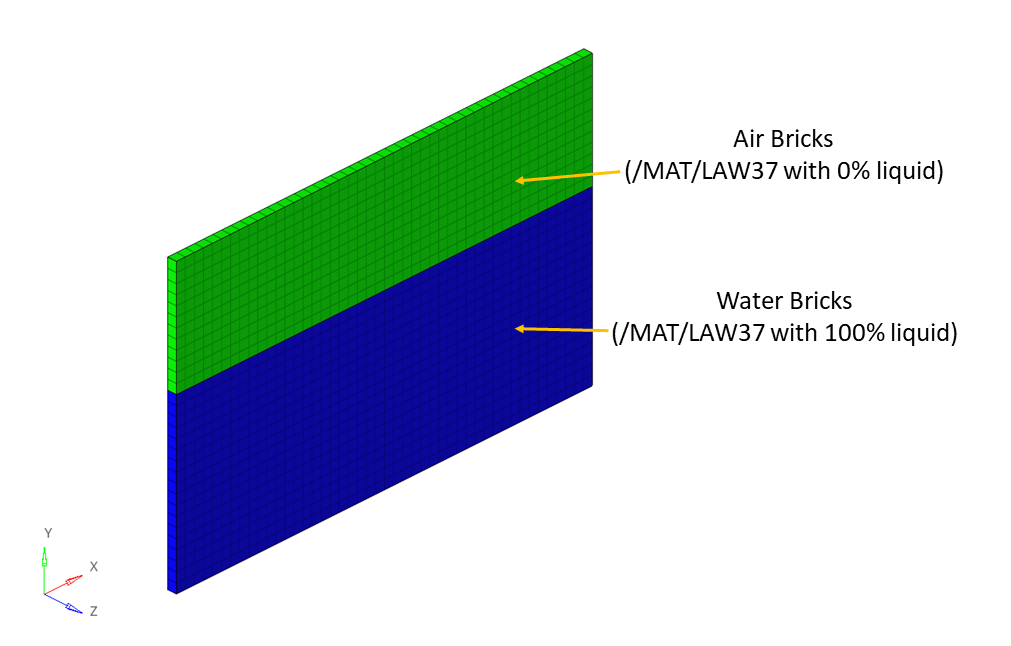
図 3. 空気と水のメッシュ(ALEソリッド)
ALE定式化を用い、ソリッドメッシュはタンクの変形によってのみ変形し、水がメッシュ内を流れます。Lagrangeシェル節点は材料のポイントに一致し、要素は材料と共に変形します。これはLagrangianメッシュです。ALEメッシュでは、境界上の節点は境界に留まるために固定され、内部節点が移動します。
結果
曲線とアニメーション
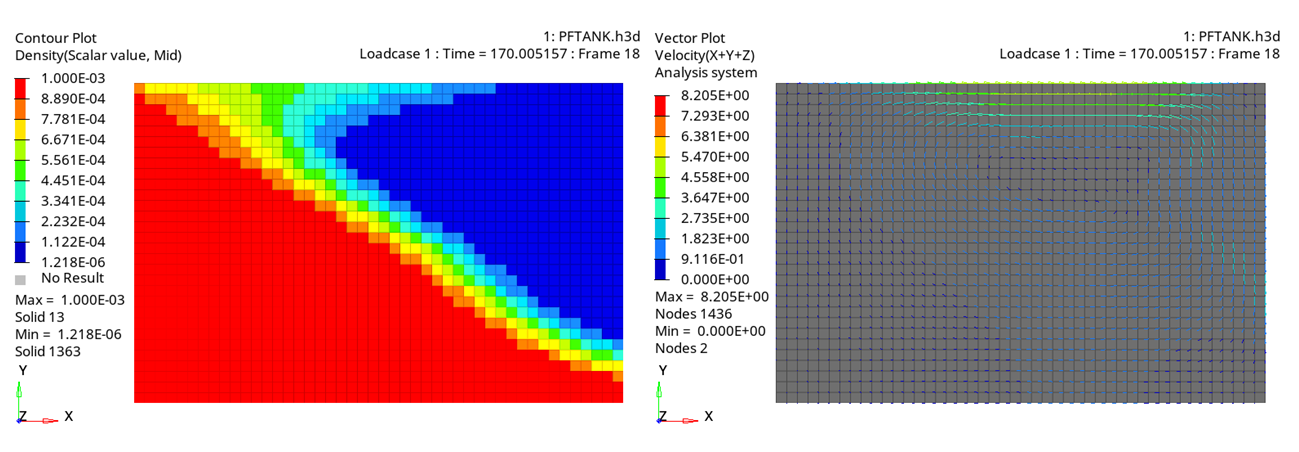 図 4. 一定加速度のモデル (重力関数1) - 時間 = 170 ms
図 4. 一定加速度のモデル (重力関数1) - 時間 = 170 ms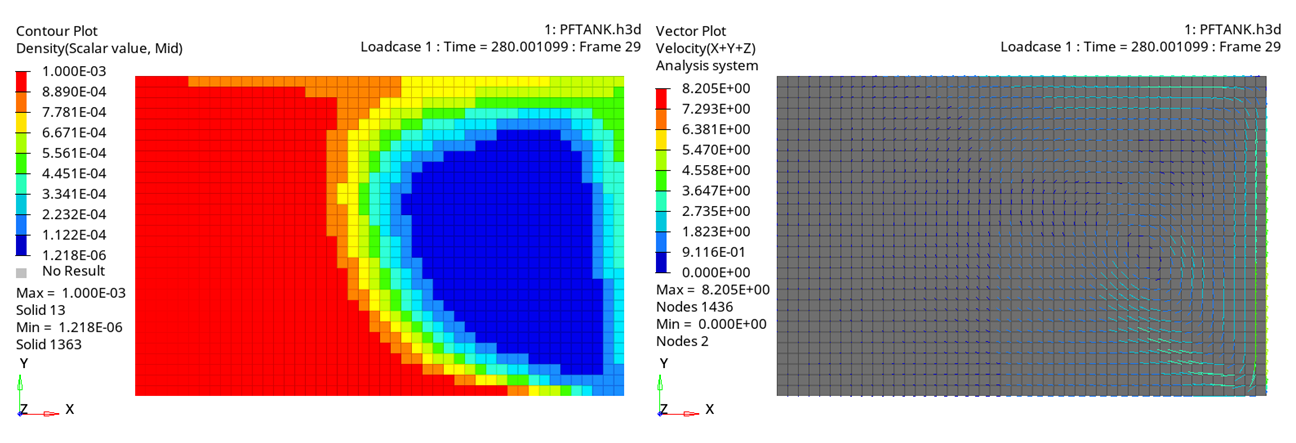 図 5. 一定加速度のモデル (重力関数1) - 時間 = 280 ms
図 5. 一定加速度のモデル (重力関数1) - 時間 = 280 ms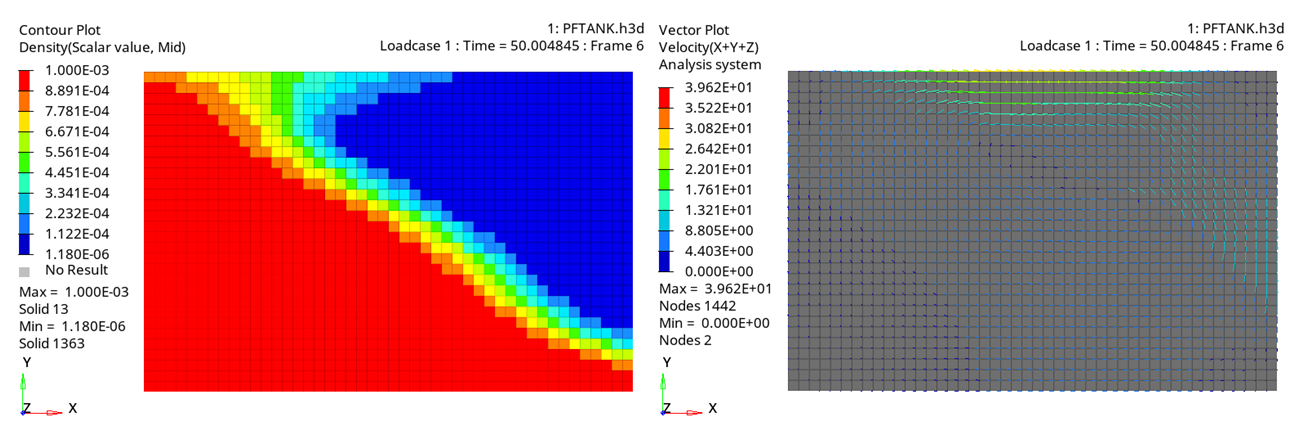 図 6. 可変加速度のモデル (重力関数2) - 時間 = 50 ms
図 6. 可変加速度のモデル (重力関数2) - 時間 = 50 ms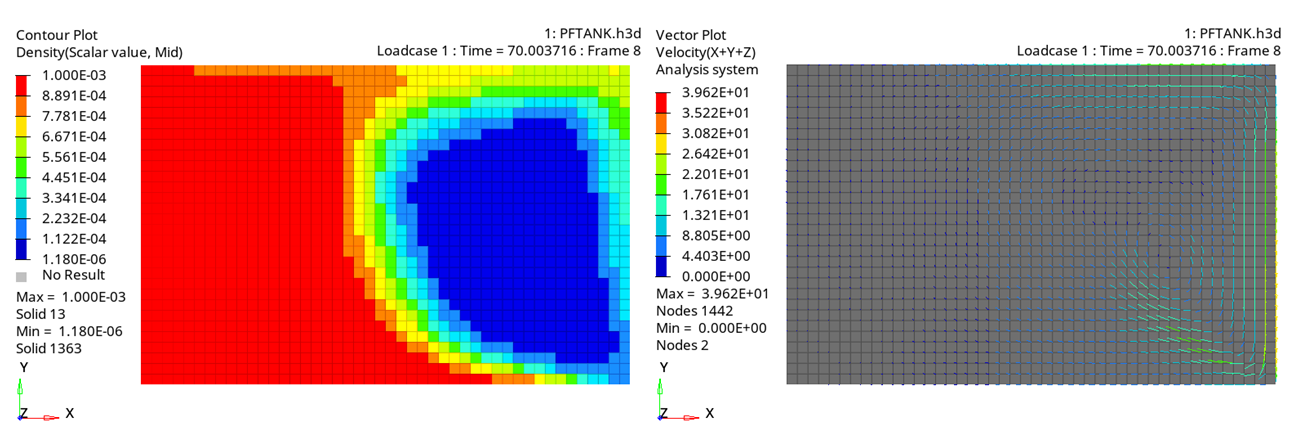 図 7. 可変加速度のモデル (重力関数2) - 時間 = 70 ms
図 7. 可変加速度のモデル (重力関数2) - 時間 = 70 msまとめ
この例題では、ALE定式を使用した流体力学的2層材料をRadiossのLAW37を用いて検討しています。ALE定式化での境界条件の適用と流体-構造相互作用の取り扱いについて議論されます。加えて、得られた結果は物理的問題を正しく表現しています。