試験体に引張力が作用します。標準化されている“ドッグボーン”試験体には、断面積が規定されています。特性の評価対象とする材料はDP600鋼です。1 試験体の右端に速度が適用されます。
単位: mm、ms、Kg、N、GPa
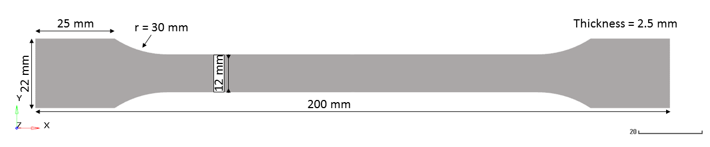
図 1. 標準化されている引張試験体の形状. 断面積は規定値
この試験体の材料は、Johnson-Cookモデル(/MAT/LAW2)で再現できる等方性弾塑性挙動を示します。表形式材料則(/MAT/LAW36)も検討されます。
この試験体のモデルを、図 2に示すように、4節点のシェルと3節点のシェルでメッシュ化します。平均の要素サイズは約2mmです。
このシェルのプロパティには、試験に適した値にする板厚部分を除き、以下の推奨のベストプラクティス設定を使用します。
- 板厚上の5つの積分点
- QEPHシェル定式化(Ishell = 24)
- 平面応力のための反復塑性(Newton-Raphson法; Iplas = 1)
- 応力計算に板厚変化を考慮(Ithick = 1)
- 初期板厚は2.5mmの一定値
境界条件
試験体の左端は、6方向の自由度(3方向の並進自由度と3方向の回転自由度)のすべてで固定されています。右端はX方向の並進のみが自由で、他の5方向の自由度はすべて固定されています。X方向に-1.0m/sの速度を、この剛体のメイン節点(
図 2に示した点)に適用し、低速で試験体の伸張量が均一に増加するようにします。

図 2. 引張試験体に適用するすべての境界条件
80mm離れた2つの測定節点(図 3)を選択し、シミュレーションで試料の測定部分に発生するの変化を継続的に測定し、試料のひずみを求めます。
工学応力(公称応力)を次の式から求めます。
(1)
ここで、
- 測定に使用した力
- 変形前の試料の断面積
工学応力の合計値を次の式から求めます。
(2)
ここで、
- 2つの測定点間長さの変化量
- 測定部分の初期長さ

図 3. 80mm離れた測定節点
真ひずみを次の関係式から求めます。
(3)
上記により、工学ひずみと真ひずみとの間には次の式が成り立ちます。
(4)
真応力は、力を真の変形後の断面で割ることにより測定できます:
(5)
したがって、真応力を計算するには断面積を考慮する必要があります。ポアソン比を0.5と仮定すると、塑性変形の間の単軸引張における真の断面積は次の式で求められます。
(6)
したがって、真応力公称応力の間の関係式は:
(7)
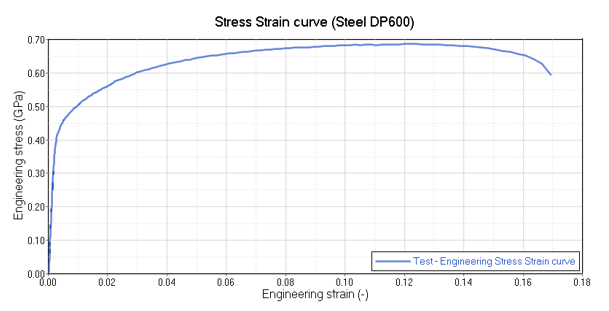
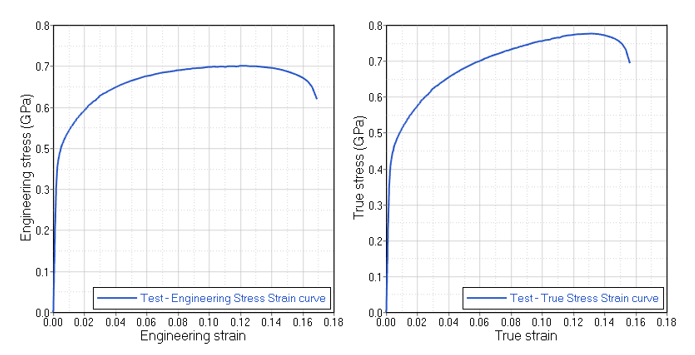
図 4. DP600鋼試験体の引張試験で得られた実験結果
材料則の特性化
材料則の特性化には2つのステップがあります。
工学応力工学ひずみ曲線から、真応力真ひずみ曲線への変換(このステップはあらゆる弾塑性材料則に適用されます)。
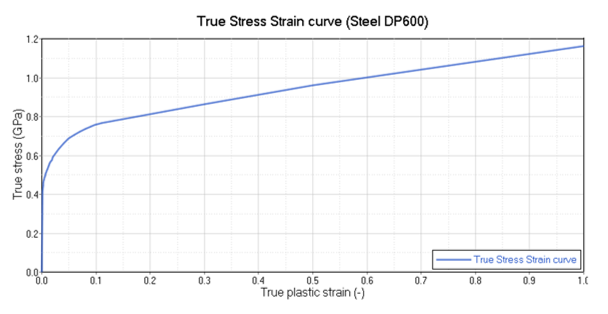
真応力対真ひずみの曲線から主なパラメーターを取り出し、材料則を定義(Johnson-Cook則と/MAT/LAW2のための材料係数、または/MAT/LAW36のための降伏曲線)。
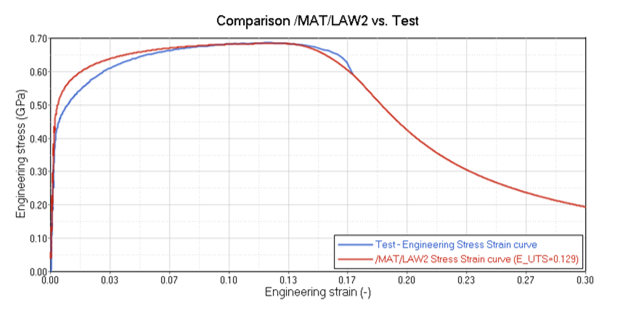
設計が早期段階であるなどの理由で材料試験データがない場合は、降伏応力、引張強度(UTS、工学応力値)、およびUTSにおける工学ひずみの各値を用意し、Iflag = 1を使用して/MAT/LAW2を特性化する必要があります。
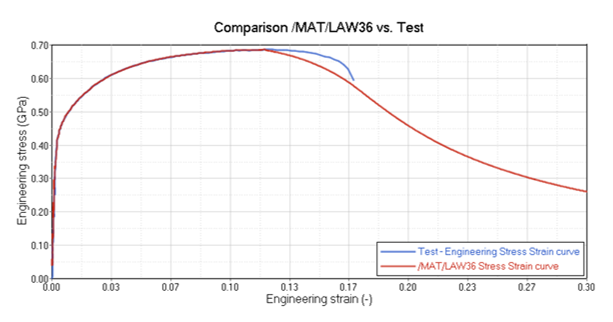
この特性化は、/MAT/LAW2(Johnson-Cook弾塑性)と/MAT/LAW36(表形式弾塑性)を対象として実施します。それぞれの材料則で、降伏応力とヤング率は曲線から決められます。
塑性ひずみは次のように定義できます:
(8)
曲線で特性化される重要なポイントはネッキングポイントで、力対変位の曲線の勾配が0になり、以下の関係式が与えられます:
(9)
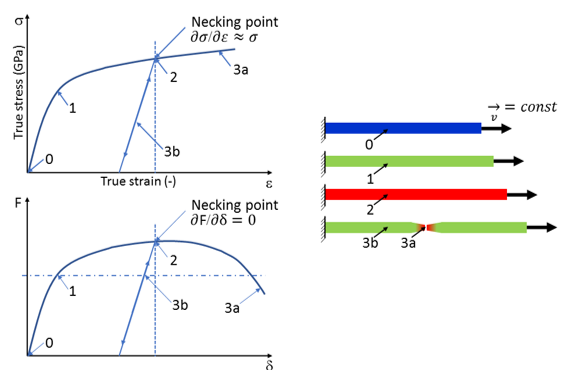
図 5. 引張試験の図式. (0~1: 弾性領域、1: 降伏点、2: ネッキングポイント、3a: 破断、3b: 線形弾性緩和)
表 1. 解析に用いられた式
| 材料特性 |
一般的な式 |
| 公称応力 |
|
| 工学ひずみ |
|
| 真応力 |
|
| 真ひずみ |
|
| 真ひずみ速度 |
|