RD-E：1701 密度

スチール製のボックスビームが、一端を固定され、他端に無限の質量で衝撃を受けます。異なる密度のメッシュの結果が比較されます。

スチール製のボックスビームが、一端を固定され、他端に無限の質量で衝撃を受けます。ボックスビームの寸法は203 mm x 50.8 mm x 38.1 mmであり、その板厚は0.914 mmです。対称性が考慮に入れられているため、構造の1/4のみがモデル化されます。

使用されるオプションとキーワード

  • シェル Q4
  • インターフェース（/INTER/TYPE7および/INTER/TYPE11）

    構造の自己接触が構造全体でのTYPE7インターフェースを用いてモデル化されます。インターフェースのメインサーフェスはモデル全体を用いて定義されています。セカンダリ節点グループはメインサーフェスを用いて定義されます。

    ビームの上部で、起こり得るエッジ-エッジ接触がTYPE11セルフインパクトインターフェースを用いて取り扱われます。そのエッジにはTYPE7インターフェースのメインサーフェスが入力のサーフェスとして用いられます。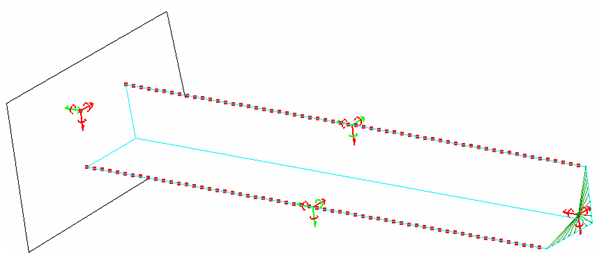

    fig_17-3
    図 1. 境界条件
  • グローバル塑性、反復塑性、可変板厚
  • BT_TYPE1、3、4、 QEPH、 BATOZ、 DKT18 と C0 定式化
  • 境界条件（/BCS）

    対称性を考慮して、Y-Z平面内の全ての節点はY方向並進とXとZ軸周りの回転が拘束されます。構造の1/4がモデル化されます。

  • 剛壁（/RWALL）

    インパクタはZ-方向の強制速度（13.3 m/s）を用いたスライド剛壁でモデル化され、他の並進と回転は固定されます。

  • 強制速度（/IMPVEL）
  • 剛体（/RBODY）

    下（固定）端は、全ての下端の点（Z = 0.0）を結合する剛体を用いてモデル化されます。剛体は並進と回転が完全に拘束されます。

入力ファイル

Before you begin, copy the file(s) used in this example to your working directory.

モデル概要

単位： mm、ms、g、N、 MPa

用いた材料は等方性弾塑性材料（/MAT/LAW2）でJohnson-Cook塑性モデルに従い、以下の特性値を持ちます：
材料特性
値
初期密度
7.8 x 10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
ヤング率
210000 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
ポアソン比
0.3
降伏応力
206 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
硬化パラメータ
450 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
硬化指数
0.5
最大応力
340 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@

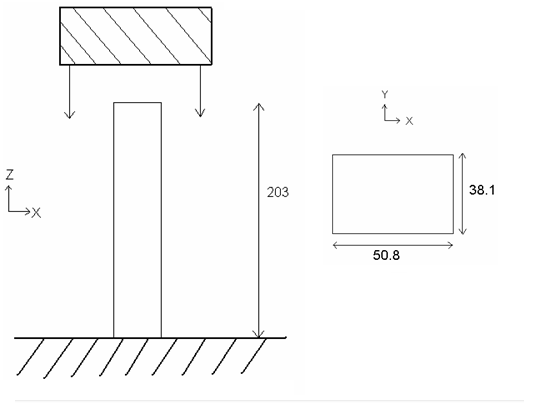
fig_17-1
図 2. 検討された問題

モデリング手法

ビームのモデル化に4タイプのメッシュが用いられます。初期メッシュはトータル60 x 8要素を用いた均一なメッシュです。他の3つのメッシュは、図 3に示すようにその要素の長さが2、3、4倍されています。

それぞれのモデルで、複数の要素定式化がテストされます：
  • BT_TYPE1
  • BT_TYPE3
  • BT_TYPE4
  • QEPH
  • BATOZ
  • C0（T3 要素）
  • DKT18（T3 要素）

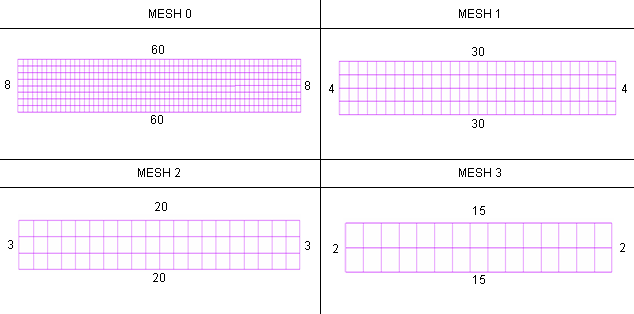
fig_17-2
図 3. メッシュ

3節点シェルメッシュは4節点シェル要素を分割して得られます。

結果

結果は2つの異なる視点を用いて比較されます：
  • 与えられたタイプの要素定式化に対するメッシュの役割と影響。
  • 与えられたメッシュに対するシェル要素定式化。
3つの基準で得られた結果の品質が比較されます：
  • 圧壊力対変位

    圧壊力はインパクタ（剛壁）のZ-方向の法線方向力に相当し、対称性から4倍されます。

    比較では、剛壁のメイン節点のZ-方向移動が変位に相当します。

  • アワグラスエネルギー
  • 全エネルギー

    全エネルギーは全てのエネルギーの合計です。

与えられたシェルでのメッシュの影響


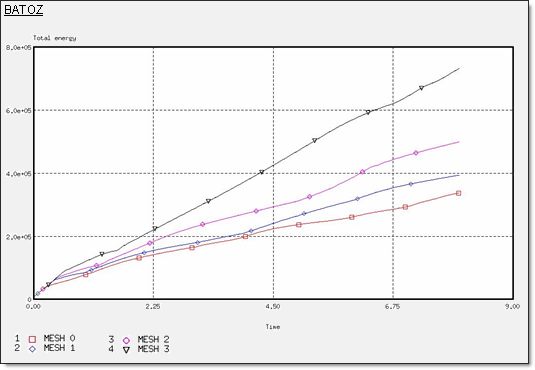
fig_17-4
図 4. BATOZ定式化での全エネルギー

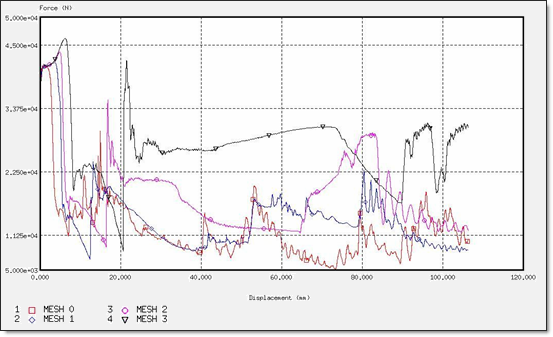
fig_17-5
図 5. BATOZ定式化での力

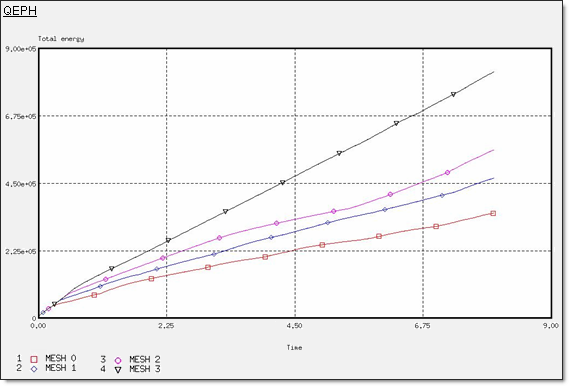
fig_17-6
図 6. QEPH定式化での全エネルギー

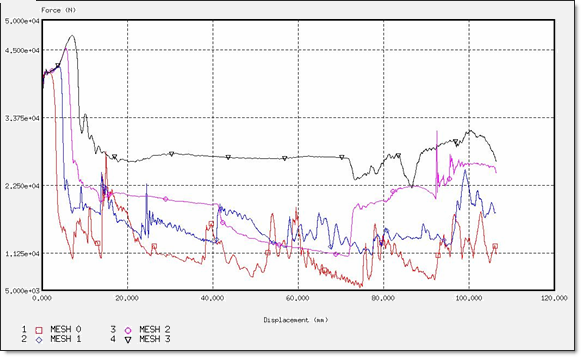
fig_17-7
図 7. QEPH定式化での力

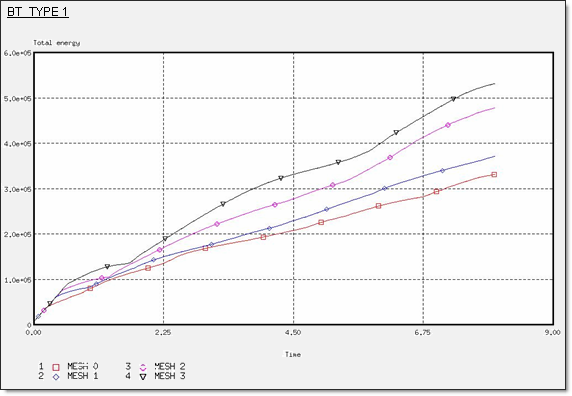
fig_17-8
図 8. BT_TYPE1定式化での全エネルギー

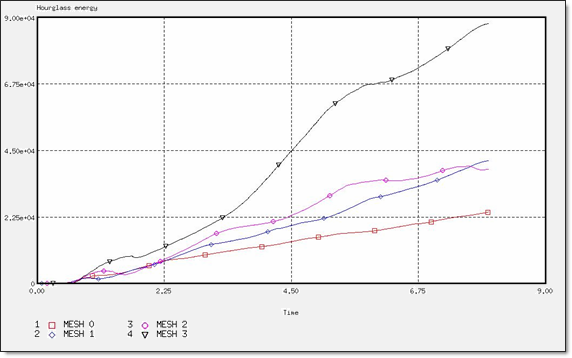
fig_17-9
図 9. BT_TYPE1定式化でのアワグラスエネルギー

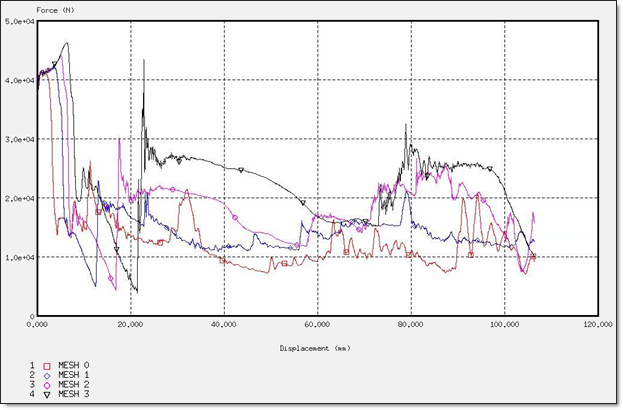
fig_17-10
図 10. BT_TYPE1定式化での力

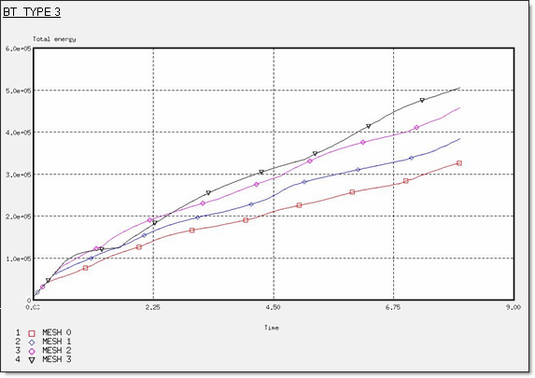
fig_17-11
図 11. BT_TYPE3定式化での全エネルギー

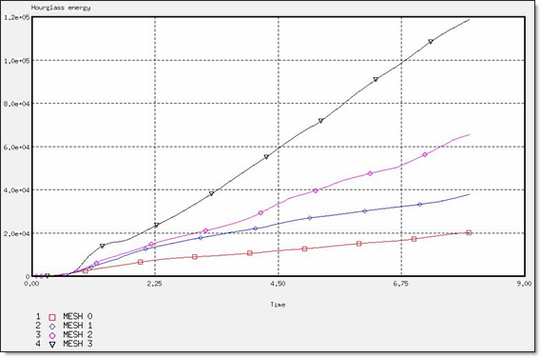
fig_17-12
図 12. BT_TYPE3定式化でのアワグラスエネルギー

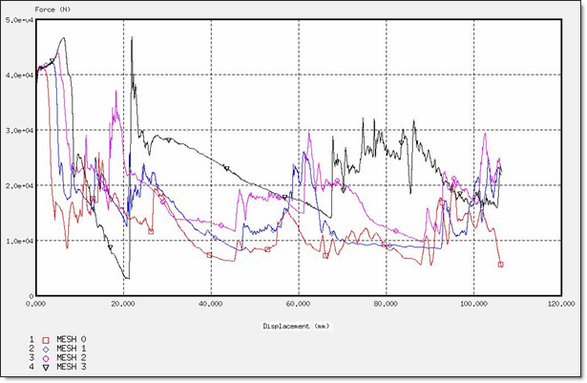
fig_17-13
図 13. BT_TYPE3定式化での力

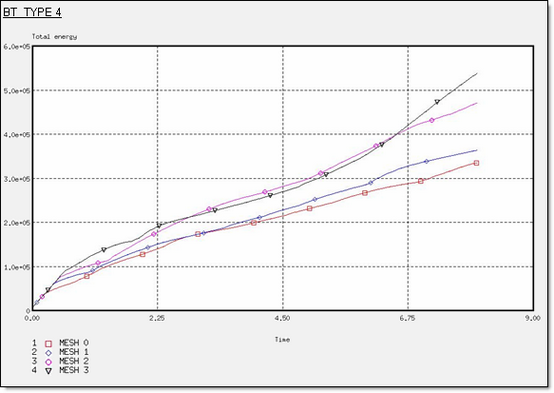
fig_17-14
図 14. BT_TYPE4定式化での全エネルギー

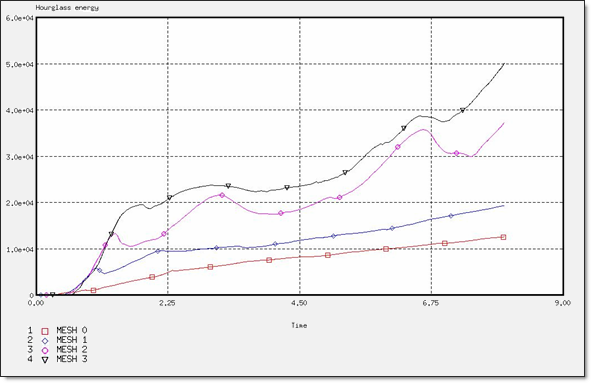
fig_17-15
図 15. BT_TYPE4定式化でのアワグラスエネルギー

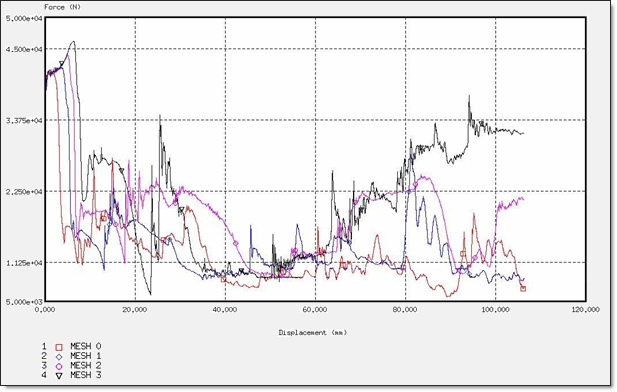
fig_17-16
図 16. BT_TYPE4定式化での力

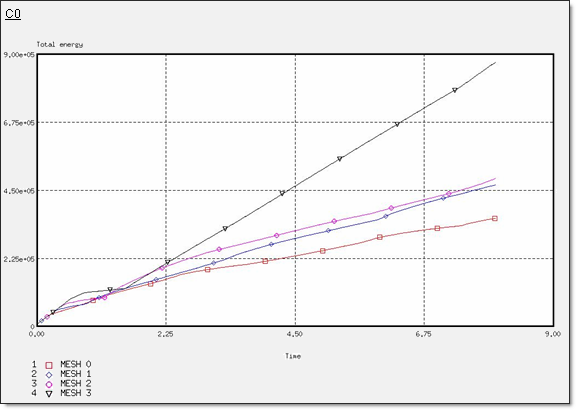
fig_17-17
図 17. CO定式化での全エネルギー

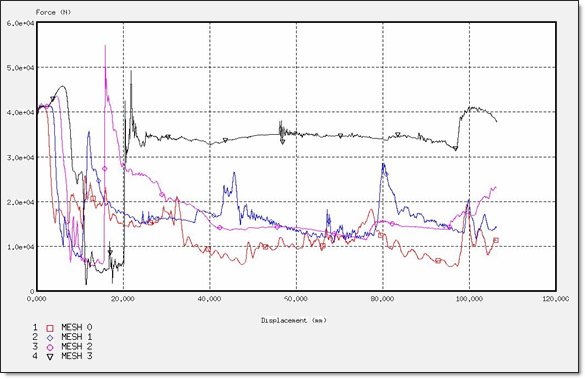
fig_17-18
図 18. CO定式化での力

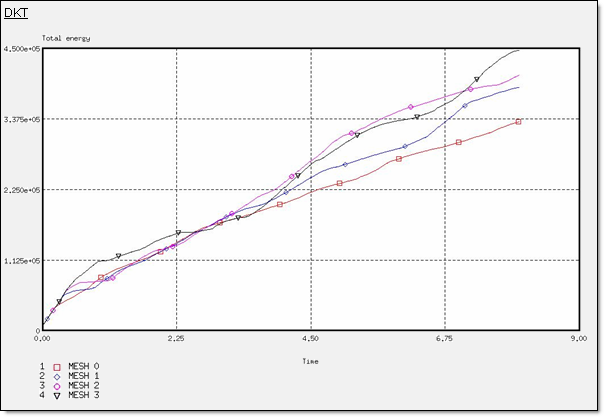
fig_17-19
図 19. DKT定式化での全エネルギー

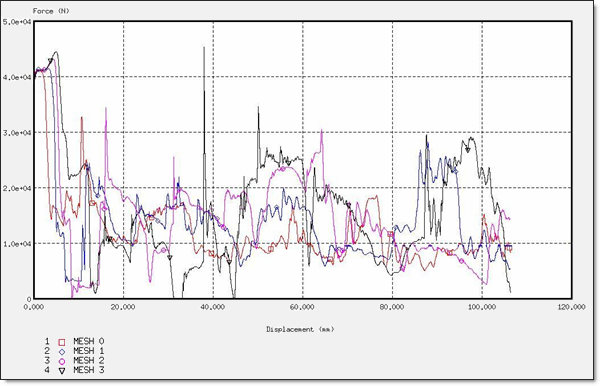
fig_17-20
図 20. DKT定式化での力

メッシュ3を用いた要素定式化の影響


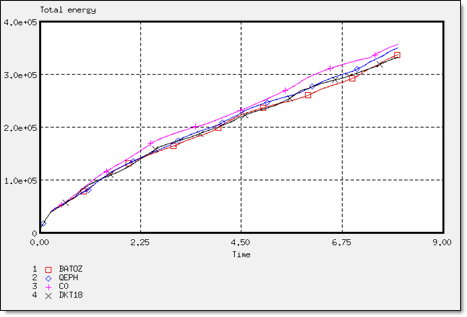
fig_17-21
図 21. 異なる定式化での全エネルギー

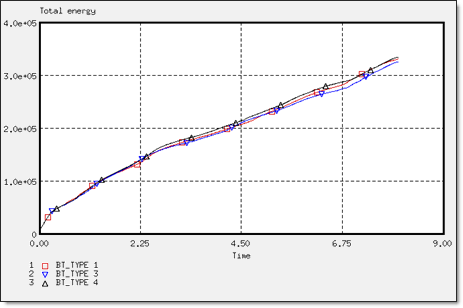
fig_17-22
図 22. 異なる定式化での全エネルギー

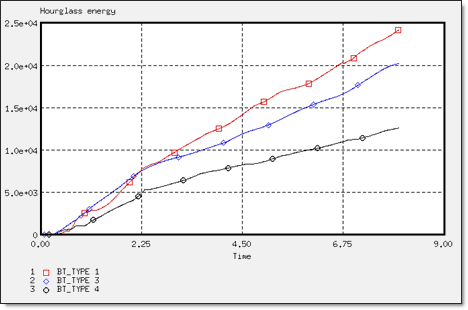
fig_17-23
図 23. 異なる定式化でのアワグラスエネルギー

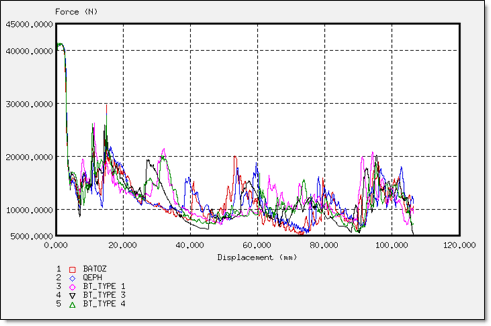
fig_17-24
図 24. 異なる要素定式化での変位

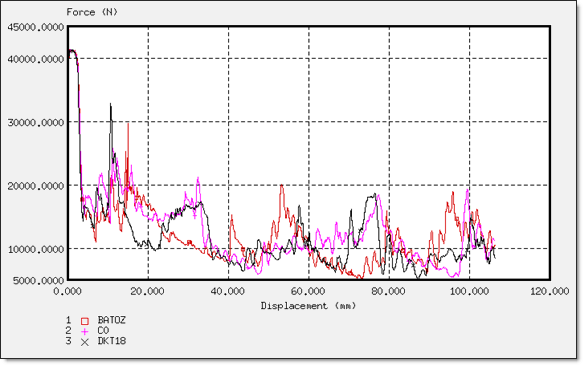
fig_17-25
図 25. 異なる要素定式化での変位

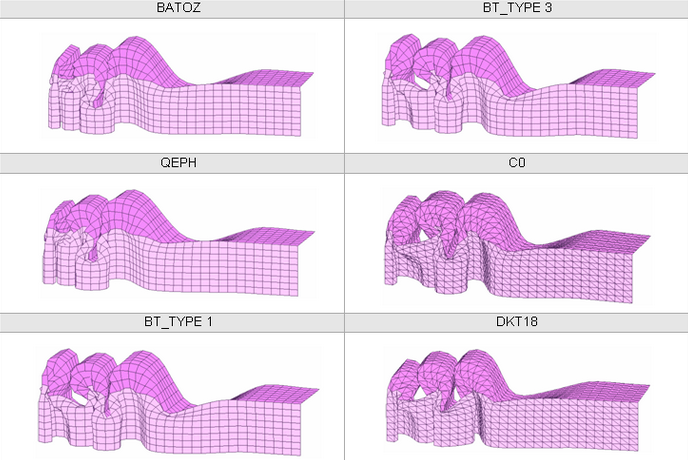
ex_17_mesh_0
図 26. メッシュ 0

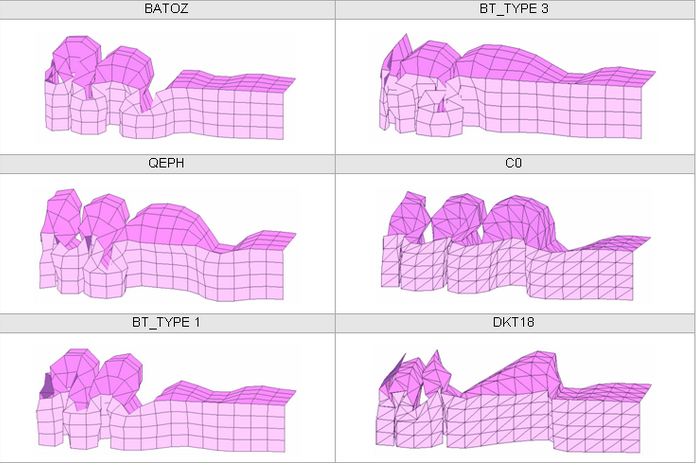
ex_17_mesh_1
図 27. メッシュ 1

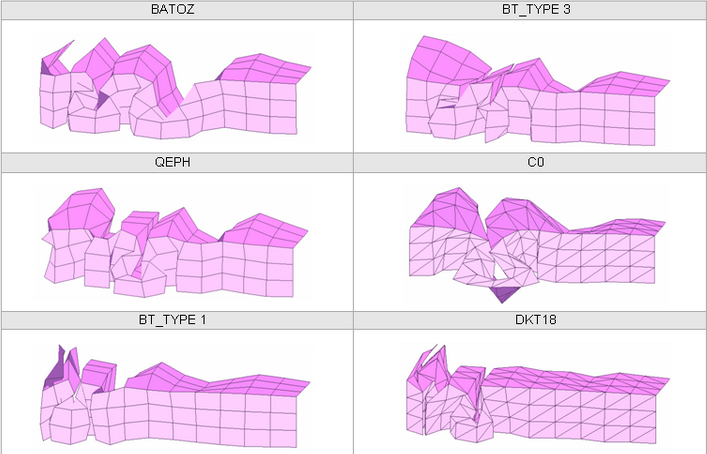
ex_17_mesh_2
図 28. メッシュ 2

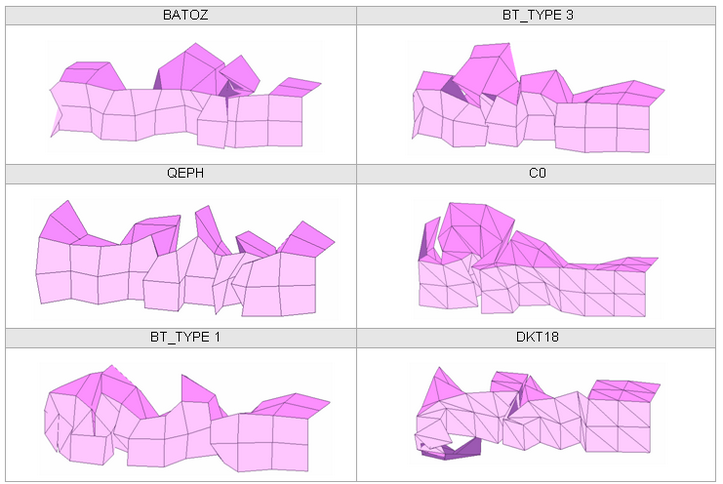
ex_17_mesh_3
図 29. メッシュ 3
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.25 x 105 3.82 x 105 4.88 x 105 7.23 x 105
Ehr

t = 8 ms

 - - - -
EK

t = 8 ms

 1.32 x 104 1.23 x 104 1.26 x 104 1.10 x 104
全エネルギー 3.38 x 105 3.94 x 105 5.00 x 105 7.34 x 105
誤差

t = 8 ms

 0.3% 1.1% 1.6% 2.9%
壁の最大法線方向力 （N） 10350 10491 10953 11555
表 1. 定式化：QEPH
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.38 x 105 4.55 x 105 5.49 x 105 8.13 x 105
Ehr

t = 8 ms

 - - - -
EK

t = 8 ms

 1.32 x 104 1.36 x 104 1.35 x 104 0.93 x 104
全エネルギー 3.51 x 105 4.68 x 105 5.63 x 105 8.23 x 105
誤差

t = 8 ms

 2.0% 2.9% 3.2% 8.0%
壁の最大法線方向力 （N） 10345 10574 11335 11865
表 2. 定式化：BT_TYPE1
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.19 x 105 3.60 x 105 4.68 x 105 5.19 x 105
Ehr

t = 8 ms

 2.42 x 104 4.17 x 104 3.87 x 104 8.80 x 104
EK

t = 8 ms

 1.29 x 104 1.23 x 104 1.16 x 104 1.35 x 104
全エネルギー 3.32 x 105 3.72 x 105 4.79 x 105 5.32 x 105
誤差

t = 8 ms

 -6.4% -9.3% -5.8% 11.5%
壁の最大法線方向力 （N） 10344 10505 10971 11569
表 3. 定式化：BT_TYPE3
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.14 x 105 3.73 x 105 4.46 x 105 4.94 x 105
Ehr

t = 8 ms

 2.02 x 104 3.80 x 104 6.56 x 104 11.90 x 104
EK

t = 8 ms

 1.31 x 104 1.24 x 104 1.32 x 104 1.29 x 104
全エネルギー 3.27 x 105 3.85 x 105 4.60 x 105 5.07 x 105
誤差

t = 8 ms

 -5.5% -8.2% -11.0% -16.7%
壁の最大法線方向力 （N） 10353 10526 11000 11670
表 4. 定式化：BT_TYPE4
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.23 x 105 3.52 x 105 4.60 x 105 5.26 x 105
Ehr

t = 8 ms

 1.26 x 104 1.94 x 104 3.74 x 104 5.02 x 104
EK

t = 8 ms

 1.30 x 104 1.24 x 104 1.21 x 104 1.31 x 104
全エネルギー 3.36 x 105 3.64 x 105 4.72 x 105 5.39 x 105
誤差

t = 8 ms

 -3.3% -4.0% -5.8% -6.5%
壁の最大法線方向力 （N） 10344 10538 11011 11568
表 5. 定式化：C0
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.45 x 105 4.56 x 105 4.79 x 105 8.64 x 105
Ehr

t = 8 ms

 - - - -
EK

t = 8 ms

 1.29 x 104 1.30 x 104 1.10 x 104 1.12 x 104
全エネルギー 3.58 x 105 4.69 x 105 4.90 x 105 8.75 x 105
誤差

t = 8 ms

 0.2% 0.8% 1.7% 2.5%
壁の最大法線方向力 （N） 10355 10344 10875 11435
表 6. 定式化：DKT18
  メッシュ 0 メッシュ 1 メッシュ 2 メッシュ 3
EI

t = 8 ms

 3.21 x 105 3.75 x 105 3.97 x 105 4.32 x 105
Ehr

t = 8 ms

 - - - -
EK

t = 8 ms

 1.29 x 104 1.34 x 104 1.13 x 104 1.45 x 104
全エネルギー 3.34 x 105 3.88 x 105 4.08 x 105 4.47 x 105
誤差

t = 8 ms

 0.5% 0.8% 1.6% 1.9%
壁の最大法線方向力 （N） 10348 10367 10800 11139

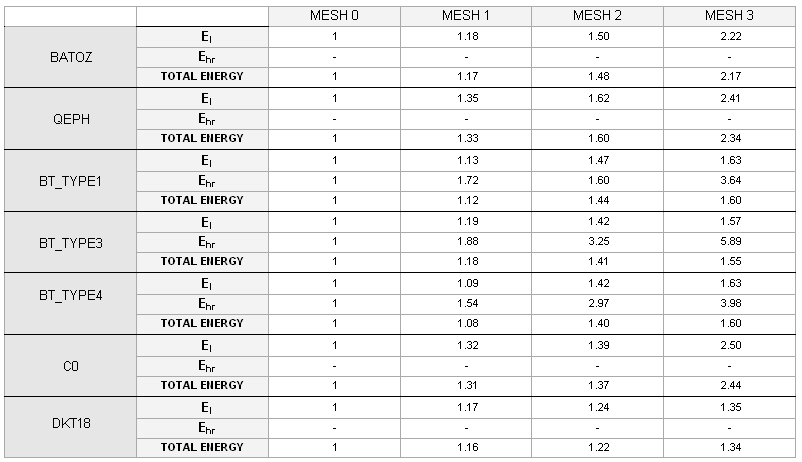
ex_17_mesh_table2-1
図 30.

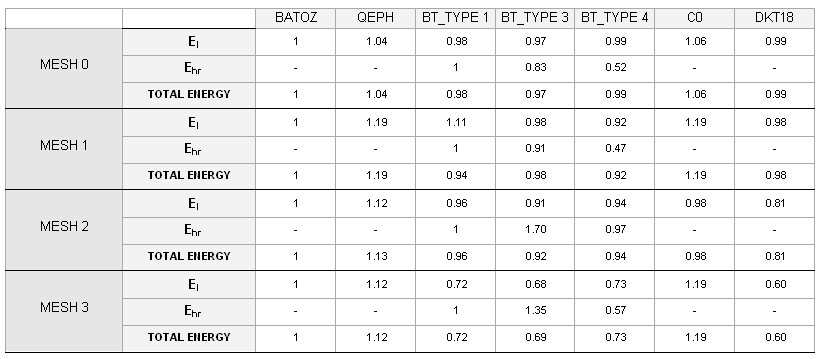
ex_17_mesh_table2-2
図 31.