/FAIL/ALTER

ブロックフォーマットキーワードフロントグラスなどガラス用途のための高度な非線形応力ベースの破壊基準。

破壊応力は、微小亀裂および亀裂伝播速度を定義するパラメータによって表されます。X-FEMでは、応力は亀裂方向に垂直で0に設定されます。

フォーマット

(1)	(3)	(5)	(7)	(8)	(9)	(10)
/FAIL/ALTER/`mat_ID`/`unit_ID`
`Exp_n`	`V0`	`Vc`	`Ncycles`	`Irate`	`Iside`	`mode`
`Cr_foil`	`Cr_air`	`Cr_core`	`Cr_edge`		`grsh4N`	`grsh3N`
`K`_IC	`K`_TH	`Rlen`	`T`_delay		`Iout`
`Kres1`	`Kres2`
`Eta1`	`Beta1`	`Tau1`	`Area_ref`
`Eta2`	`Beta2`	`Tau2`
`Sig0`	`P_scale`	`P_switch`

オプションの行

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fail_ID`

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	（オプション）単位識別子（整数、最大10桁）
`Exp_n`	亜臨界亀裂進展の亀裂進展指数デフォルト = 16.0（実数）
`V0`	`K`_ICにおける亜臨界亀裂進展の亀裂進展速度 $V_{0}$ 。デフォルト = 0.0（実数）	$[\frac{m}{s}]$
`Vc`	最大亀裂進展速度ガラスデフォルト = 0.0（実数）	$[\frac{m}{s}]$
`Ncycles`	反復する応力フィルタリング期間。`Irate`=0の場合にのみ使用されます。 2 = 1（デフォルト）フィルタリングなし（整数）
`Irate`	応力速度フィルタリング手法 = 0 `Ncycles`を用いた指数移動平均 = 1 最後の50サイクルを用いた算術平均（整数）
`Iside`	ひずみ速度依存オプション = 0（デフォルト）空気（外向き）側のみのひずみ速度依存。 = 1 シェルの両側のひずみ速度依存。（整数）
`mode`	近傍の要素間の破壊進展モデルを切り替えるためのフラグ = 0（デフォルト）破壊進展なし = 1 XFEM破壊進展 = 2 等方性フロントウェーブ進展 = 3 要素エッジを介した方向進展 = 4 エッジと対角線を介した方向進展（整数）
`Cr_foil`	下部サーフェスにおける亀裂深さデフォルト = 0.0（実数）	$[m]$
`Cr_air`	上部サーフェスにおける亀裂深さデフォルト = 1.0（実数）	$[m]$
`Cr_core`	底部とサーフェスの積分点の間の亀裂深さデフォルト = 1.0（実数）	$[m]$
`Cr_edge`	ウィンドシールドのエッジ要素における亀裂深さデフォルト = 1.0（実数）	$[m]$
`grsh4N`	（オプション）4節点エッジシェル要素のグループ識別子デフォルト = 0（整数）
`grsh3N`	（オプション）3節点エッジシェル要素のグループ識別子デフォルト = 0（整数）
`K`_IC	破壊靭性デフォルト = 0.0（実数）	$[P a \sqrt{m}]$
`K`_TH	疲労のしきい値デフォルト = 0.0（実数）	$[P a \sqrt{m}]$
`Rlen`	参照長さデフォルト = 1.0（実数）	$[m]$
`T`_delay	要素を削除する前の緩和時間。デフォルト = 0.0（実数）	$[s]$
`Iout`	Engine出力ファイルで完全破壊フラグをアクティブにします。 = 0（デフォルト）追加の出力はありません。 = 1 拡張出力をアクティブにします。（整数）
`Kres1`	1つ目の亀裂方向の残留引張応力スケールファクター。デフォルト = 0.0（実数）
`Kres2`	2つ目の亀裂方向の残留引張応力スケールファクター。デフォルト = 0.0（実数）
`Eta1`	下部サーフェスの分布パラメータ $η_{1}$ 。 10 （実数）	$[Pa]$
`Beta1`	下部サーフェスの分布パラメータ $β_{1}$ 。 10 （実数）
`Tau1`	下部サーフェスの分布パラメータ $τ_{1}$ 。 10 （実数）	$[Pa]$
`Area_ref`	参照要素サーフェス面積。（実数）	$[m^{2}]$
`Eta2`	上部サーフェスの分布パラメータ $η_{2}$ 。 10 （実数）	$[Pa]$
`Beta2`	上部サーフェスの分布パラメータ $β_{2}$ 。 10 （実数）
`Tau2`	上部サーフェスの分布パラメータ $τ_{2}$ 。 10 （実数）	$[Pa]$
`Sig0`	ガラス表面の初期応力。（実数）	$[Pa]$
`P_scale`	選択した分布関数の定義区間を制限します。（0.0と1.0の間の実数）
`P_switch`	分布関数の区間： = 0 分布関数fromは、(0, `P_scale`)の間で定義されます。 = 1 分布関数fromは、(`P_scale`, 1)の間で定義されます。（整数）
`fail_ID`	破壊基準識別子 9 （整数、最大10桁）

例（ガラス）

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
#              MUNIT               LUNIT               TUNIT
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW36/72200103/1
Glass with linear hardening
#              RHO_I
             2.50E-9
#                  E                  NU           Eps_p_max               Eps_t               Eps_m
             70000.0                0.23                   0                   0                   0 
#  N_funct  F_smooth              C_hard               F_cut               Eps_f
         1         1                   0                1650                   0
#  fct_IDp              Fscale   fct_IDE                EInf                  CE
         0                   0         0                   0                   0
#  fct_ID1   fct_ID2   fct_ID3   fct_ID4   fct_ID5
 722001021
#           Fscale_1            Fscale_2            Fscale_3            Fscale_4            Fscale_5
                1000
#          Eps_dot_1           Eps_dot_2           Eps_dot_3           Eps_dot_4           Eps_dot_5
                   0 
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FAIL/ALTER/72200103/1
#              EXP_N                  V0                  VC   NCYCLES     IRATE     ISIDE      MODE
                16.0                 6.0             1520000         6         0         0         1
#            CR_FOIL              CR_AIR             CR_CORE             CR_EDGE    GRSH4N    GRSH3N
             0.00040             0.00100             0.00500                   0         0         0
#                KIC                 KTH                RLEN                TDEL      Iout
              23.717              7.9057                 1.0                   0         0
#              KRES1               KRES2
                   0                   0
#               ETA1               BETA1                TAU1            AREA_REF
                   0                   0                   0                   0
#               ETA2               BETA2                TAU2
                   0                   0                   0
#               SIG0             P_SCALE  P_SWITCH
                   0                   0         0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/722001021
Function for glass
#                  X                   Y
                 0.0               500.0
                 1.0               550.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata

この破壊基準は、破壊の基準として最大応力を用いており、初期亀裂と亀裂進展速度によって決定される材料の強度に基づいて計算されます。modeスイッチフラグに応じて、近傍の要素間の異なる破壊進展モデルが使用され得ます。
Irate=0である際、指数移動平均フィルターが使用され、フィルタリングされた応力は：(1)
$σ_{f} (t) = α σ (t) + (1 - α) σ (t - Δ t)$

ここで、

$σ_{f} = filtered stress$

$α = \frac{2}{N_{c y c l e s} + 1}$
この破壊モデルは低減積分シェル要素（I_shell =24およびI_sh3n =2を推奨）とのみ適合性があり、完全積分シェル要素とは適合性を有しません。また、使用されるシェルプロパティに制限はないものの、1層シェルモデルとのみ適合します。
グループgrsh4Nおよびgrsh3N内で定義された要素は、フロントガラスのエッジに沿っていなくてはならず、特定の破壊脆弱を受けます。
この破壊モデルは、重複節点を用いてポリビニルブチラール（PVB）ソリッド要素の層を挟むシェル要素に適用されます。アセンブリ全体がフロントガラスをモデル化します。

図 1. フロントガラスの有限要素モデル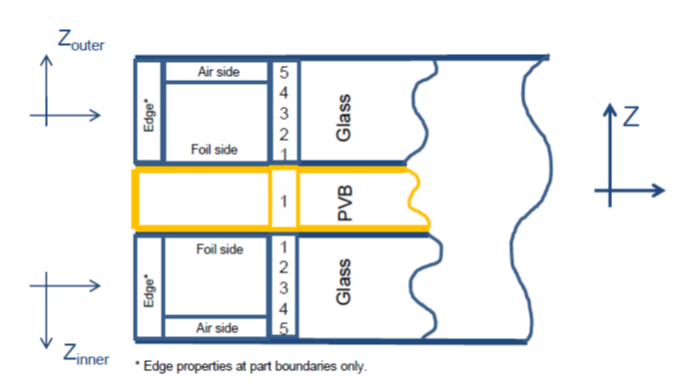

図 2. フロントガラスモデル - アセンブリ全体
この破壊モデルを用いたシェル要素は、法線が中間PVBから離れる方向を指すよう方向付けされていなくてはなりません。
シェル要素には、曲げを正しくモデル化するために、オフセットが適用される必要があります。これは、/PROP/TYPE51 I_pos=4を用いて行うことができます。
破壊限界は、その位置および周りの要素の破壊状態に依存します。 ¹
fail_IDは、/STATE/BRICK/FAILと/INIBRI/FAILおよび/PERTURB/FAIL/BIQUADと共に使用されます。デフォルト値はありません。この行が空白の場合、/INIBRI/FAIL内の破壊モデル変数のために出力される値はありません（3次元ソリッドの場合は/STATE/BRICK/FAIL、シェルの場合は/STATE/SHELL/FAILで.staファイルに書き込まれます）。
Ch. Brokmann拡張²は、外部ガラス表面のみを対象にした破壊基準を追加定義します。これにより、機械的処理または化学的処理により発生するガラス表面の初期応力を定義します。ガラス表面の微小欠陥の統計的評価により、ワイブル確率分布（left-truncated）を使用して破壊の確率を定義できます。
ここで、 $i$ = 1、2 （下部および上部のサーフェスの場合） (2)
$P (σ) = 1 - \exp [{(\frac{τ_{i}}{η_{i}})}^{β_{i}} - {(\frac{σ}{η_{i}})}^{β_{i}}]$

切り捨て点 $τ = 0$ では、よく知られている2パラメータワイブル分布が得られます。Brokmannモデルは、ガラス内のランダムに配向された初期欠陥を計算し、それらをさまざまな長さと形状を持つすべての有限要素に配分します。亀裂の成長は、次の微分方程式で表すことができます： (3)
$d a = V_{0} . {(\frac{Y σ \sqrt{π a}}{K_{I C}})}^{E x p_n} d t$

ここで、 $Y$ はワイブル分布を使用して求めた欠陥形状係数です。

式 3を積分すると、応力速度に強く依存する実際の亀裂サイズが得られます。実際の応力拡大係数を計算して、破壊基準で使用することができます。

Brokmannのモデルの面白さは、分布パラメータと破壊応力値によって、破壊の確率的な可能性を推定できることです。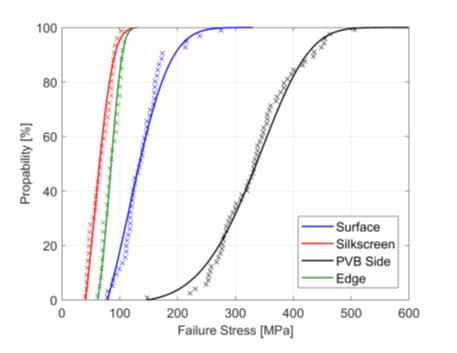

図 3.

ガラスの欠陥をランダムに初期化して十分な回数のシミュレーションを実行した後、頭部損傷基準（HIC）の特定の値に到達する確率を推定する可能性を返します。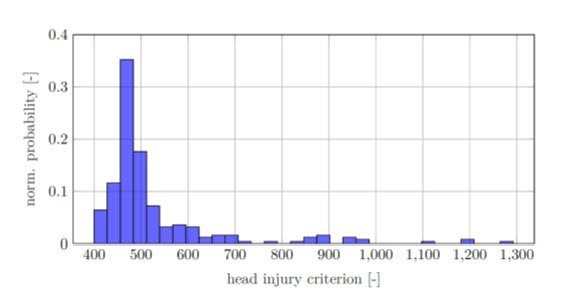

図 4.
Ch. Brokmann基準を使用すると、フラグIrateは自動的に0に設定されます。この場合、指数平均を使用して、応力フィルタリング区間のサイクル数を定義する必要があります。

¹ Alter, Christian, Stefan Kolling, and Jens Schneider."An enhanced non–local failure criterion for laminated glass under low velocity impact."International Journal of Impact Engineering 109 (2017): 342-353.

² Ch.Brokmann: “A Model for the Stochastic Fracture Behavior of Glass and Its Application to the Head Impact on Automotive Windscreens”, Springer Vieweg, 2022, ISBN 9783658367879

/FAIL/ALTER

フォーマット

定義

例（ガラス）

コメント