/FAIL/SYAZWAN
ブロックフォーマットキーワード この簡素化された破壊基準は、線形損傷累積を伴う破壊サーフェスに基づいています。また、線形ひずみ経路を想定し、ひずみ履歴を使用した損傷値の初期化も提供します。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /FAIL/SYAZWAN/mat_ID/unit_ID | |||||||||
| IcardIcard | εfpMIN | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | |||||
| C6 | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| εcompf | εshearf | εtensf | εplanef | εbiaxf | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Dinit | Dsf | Dmax | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Inst | Iform | Nvalue | Softexp | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDEl | El_ref | Fscale_El | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fail_ID |
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| mat_ID | 材料識別子 (整数、最大10桁) |
|
| unit_ID | (オプション)単位の識別子。 (整数、最大10桁) |
|
| Icard | カード入力フォーマットのフラグ。 3
(整数) |
|
| εfpMIN | 破壊時の最小塑性ひずみ。 デフォルト = 0.0(実数) |
|
| C1 | 破壊サーフェスの第1定数。 (実数) |
|
| C2 | 破壊サーフェスの第2定数。 (実数) |
|
| C3 | 破壊サーフェスの第3定数。 (実数) |
|
| C4 | 破壊サーフェスの第4定数。 (実数) |
|
| C5 | 破壊サーフェスの第5定数。 (実数) |
|
| C6 | 破壊サーフェスの第6定数。 (実数) |
|
| εcompf | 単軸圧縮の破壊時塑性ひずみ。 (実数) |
|
| εshearf | せん断の破壊時塑性ひずみ。 (実数) |
|
| εtensf | 単軸引張の破壊時塑性ひずみ。 (実数) |
|
| εplanef | 平面ひずみの破壊時塑性ひずみ。 (実数) |
|
| εbiaxf | 2軸引張の破壊時塑性ひずみ。 (実数) |
|
| Dinit | ひずみテンソルからの損傷値初期化のフラグ。
(整数) |
|
| Dsf | 損傷初期化のスケールファクター。 デフォルト = 1.0(実数) |
|
| Dmax | 損傷初期化の最大値。 デフォルト = 1.0(実数) |
|
| Inst | ネッキング不安定性のフラグ。
(整数) |
|
| Iform | ネッキング不安定性定式化のフラグ。
(整数) |
|
| Nvalue | Hollomonの法則から導出されたN値。 デフォルト = 0.25(実数) |
|
| Softexp | 応力軟化指数。 デフォルト = 1.0(実数) |
|
| fct_IDEl | 要素サイズ因子関数識別子。 (整数) |
|
| El_ref | 参照要素サイズ。 デフォルト = 1.0(実数) |
[m] |
| Fscale_El | 要素サイズ係数関数のスケールファクター。 デフォルト = 1.0 |
|
| fail_ID | (オプション)破壊基準識別子。 (整数、最大10桁) |
▸例
コメント
- /PROP/SHELLの Iplas の値を1に設定することを強くお勧めします。これにより、主ひずみ速度 β の正確な計算が可能になります。
- C1、C2、C3、C4、C5、C6の値は、以下に基づきます:
(1) εfp=C1+C2η+C3ˉθ+C4η2+C5ˉθ2+C6ηˉθここで、- εfp
- 破壊時の塑性ひずみ。
- η
- 以下のように表される応力軸性 η=13(σxx+σyy)σVM
- ˉθ
- 正規化されたLode角 ˉθ=1−2πarcosζ
ここで、 σVM はフォンミーゼス応力です。
図 1 は、平面応力破壊曲線を破壊サーフェス基準に対して曲線フィッティングする例を示しています。図 1. Syazwan破壊基準フィッティングの例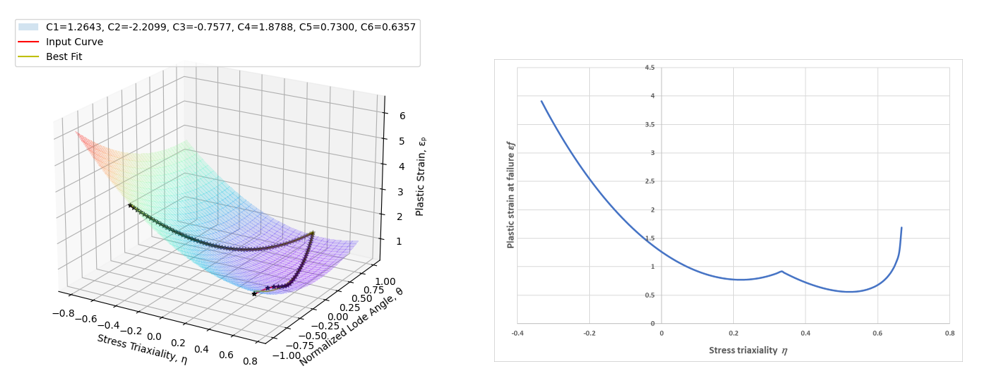
-
Icard
の値に応じて、2種類のパラメータ入力カードフォーマットが/FAIL/SYAZWANで使用可能です。
- Icard = 1の場合: Ciパラメータを直接入力する必要があります。
-
Icard
= 2の場合: 次の一般的にテストされている複数の荷重条件に対して破壊時の塑性ひずみを指定できます: 単軸圧縮
εcompf
、せん断
εshearf
、単軸引張
εtensf
、面ひずみ
εplanef
、2軸引張
εbiaxf
。この場合、以下の連立方程式を解くことで、Ciパラメータは自動的に計算されます:
(2) {C1−13C2−C3+19C4+C5+13C6=εcompfC1=εshearfC1+13C2+C3+19C4+C5+13C6=εtensfC1+1√3C2+13C4=εplanefC1+23C2−C3+49C4+C5−23C6=εbiaxfC2−18πC3+2√3C4−18π√3C6=0
注: 最後の式では、平面ひずみ条件がこの破壊基準の局所最小値に対応していることが要求されます。 - 場合によっては、一部の荷重条件について、この基準の値が負になったり非常に小さくなったりすることがあります。その場合、正または0である必要がある破壊時の最小塑性ひずみパラメータ
εfpMIN
(デフォルト値は0.0)によって、この基準が制限されます。
εfpMIN
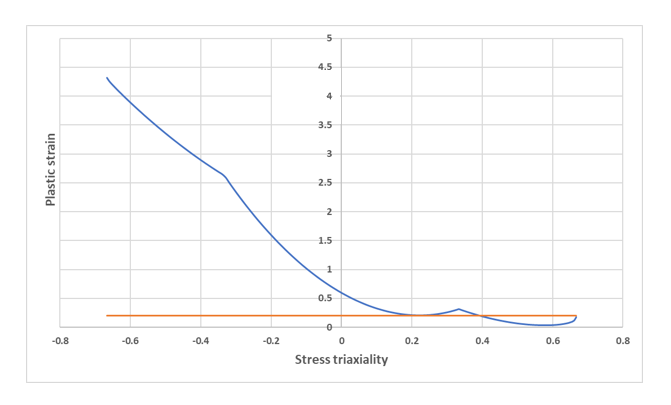
より小さい値はすべて無視されます。 図 2 は、0.2という最小値(オレンジ色の曲線)での例を示しています。図 2. 破壊時塑性ひずみの2.0という最小値(オレンジ色の曲線)によって制限された破壊基準. εfpMIN (青色の曲線)
- 損傷変数の進展は、次のように増分的に計算されます:
(3) D=∞∑t=0Δεpεfp - 既存の合計フィールドと塑性ひずみフィールドから始まるシミュレーションを実施することもできます(前の成形シミュレーションなどの後に)。最初のシミュレーション時に破壊基準が計算されない場合は、最初のシミュレーションの終了時に取得された全ひずみテンソル値と塑性ひずみ値から、損傷フィールドを推定できます(.staファイルを使用)。Dinitフラグが1に設定されている場合、塑性ひずみが0でなければ、損傷フィールドは計算されます。/INISHE/STRA_F、/INISHE/STRA_F、/INISHE/EPSP_F、/INISH3/EPSP_Fが、ステータスファイルのキーワード内に存在している必要があります。初期応力テンソルはシミュレーションモデルに組み込まれていないため、次の式を使用して応力軸性が導出されます:
(4) η=1√31+β√1+β+β2その後、次のように初期損傷値を推定できます:(6) Dt=0=εt=0pεfp図 3 は、破壊基準の計算なしで実行された成形シミュレーション後の1ステップで初期化された損傷フィールドの例を示しています。その後、損傷フィールドは、上記の塑性ひずみとひずみテンソルを使用して求められます。図 3. 成形シミュレーション後の損傷フィールドの“1ステップ”初期化の例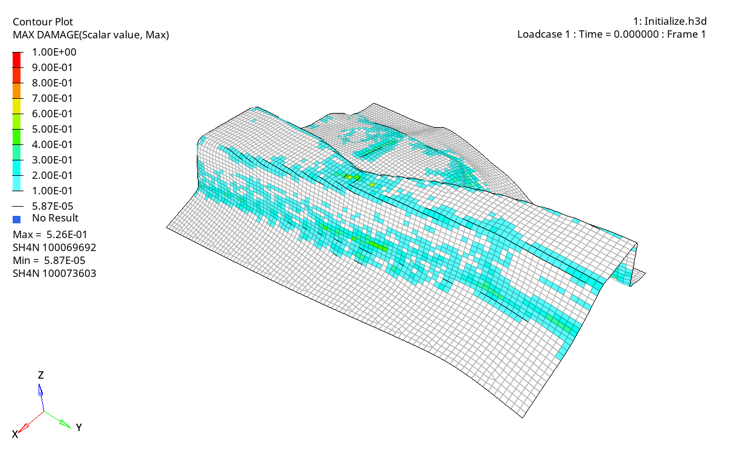
- Instフラグが1に設定されている場合は、制御されたネッキング不安定性を使用できます。この不安定性を引き起こすために、
f
と表される基準変数が、ユーザーによって指定されたNvalueに基づき、次の式を使用して計算されます:
(7) ε1=2(2−α)(1−α+α2)4−3α−3α2+4αNvalueε2=2(2α−1)(1−α+α2)4−3α−3α2+4αNvalueここで、 α は、次の式を使用して β から計算された最小主応力と最大主応力の比率です:(8) α=2β+12+βその後、ネッキング不安定性における有効塑性ひずみを次のように計算できます:(9) εinstp=ε1⋅√43(1+β+β2)パラメータNvalueは、単軸引張で取得された不安定性塑性ひずみの値です(ここで、 η=1/3 かつ ˉθ=1 )。その後、上記の β と応力軸性を結び付ける関係を使用して、不安定性ひずみの進展をプロットできます。
不安定性塑性ひずみを使用して、 f と表される不安定性基準変数が、次のいずれかで計算されます:- Iform = 1の場合、増分的に計算され、荷重履歴が考慮されます。
(10) f=∞∑t=0Δεpεinstp - Iform = 2の場合、直接計算され、荷重経路履歴が無視されます。
(11) f=εpεinstp
この基準に達した場合( f=1 )、損傷変数 D の瞬間値が、要素履歴変数になる値 Dcrit に保存されます。その後、応力軟化によってネッキング不安定性をトリガーできます。この方程式は次のとおりです:(12) D=∫ΔDf=∫ΔfDcrit={1whilef<1Dwhenf≥1σ=σeff(1−(D−Dcrit1−Dcrit)Softexp)ここで、- σ
- 損傷応力テンソル。
- σeff
- 無損傷有効応力テンソル。
- Dcrit
- 応力軟化を引き起こす限界損傷値。
- Softexp
- 指数パラメータ。
可視化のために、上記のすべての式から不安定性曲線( εinstp 対 η )を得ることができます。例えば、Nvalueが0.175に設定されている場合、次の曲線(図 4)が得られます。図 4. 不安定性曲線(オレンジ色)および破壊基準(青色)に対するこの曲線の位置の例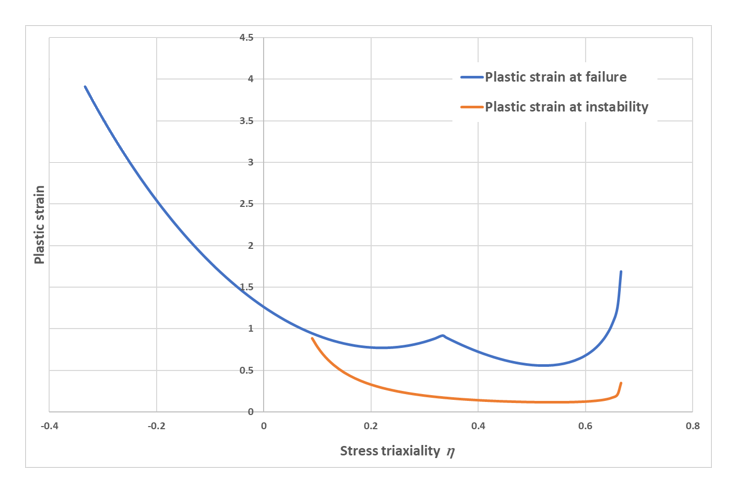
不安定性曲線の効果は正の応力軸性に制限され(ネッキングは引張でのみ発生するため)、破壊基準曲線の下にある場合にのみ効果を発揮します。
図 5 は、さまざまなNvalueパラメータ値を使用して得られたいくつかの不安定性曲線を示しています。図 5. さまざまなNvalueパラメータを使用して得られた不安定性曲線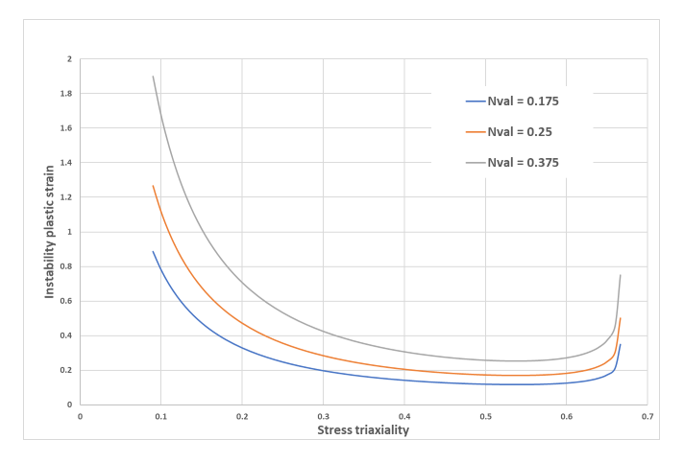
- Iform = 1の場合、増分的に計算され、荷重履歴が考慮されます。
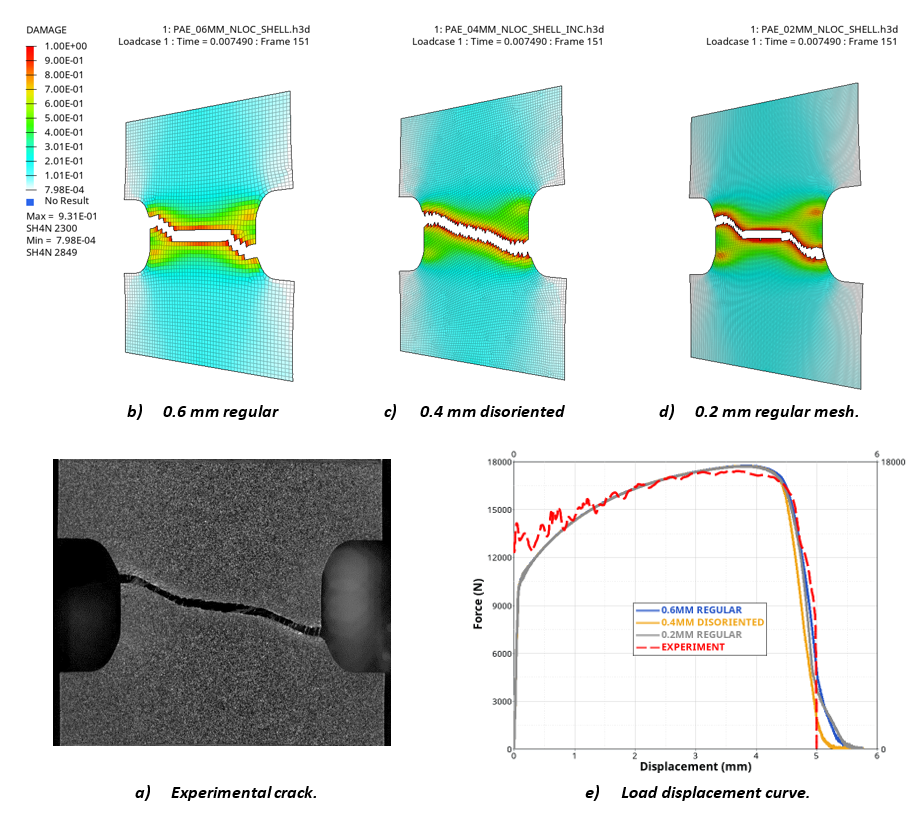
- 要素サイズスケーリングを使用して破壊を正則化し、さまざまなメッシュサイズで消散されたほぼ一定の破壊エネルギーを確実に求めることができます。この要素サイズ依存性は、関数fct_IDElで定義された
fsize
で表されるサイズスケールファクターを計算することで導入されます。このサイズスケールファクターの進展は、初期要素特性長を参照サイズEl_ref(デフォルト値は1.0)で除算した比率に対して得られます:
fsize(L0eLref)
。追加のスケールファクターFscale_Elを正則化関数全体に適用することもできます。このように計算された要素サイズのスケールファクター
fsize
は、次のように損傷変数進展方程式に(不安定性変数進展方程式が定義されている場合は、この方程式にも)導入されます:
(13) D=∞∑t=0Δεpεfp⋅fsize(L0eLref)⋅felscale - 代わりの方法として、Syazwan破壊基準(図 6)に適合している/NONLOCAL/MATオプションを使用して、メッシュのサイズと向きに従って解を正則化できます。非局所正則化が使用されている場合、非局所塑性ひずみを使用して、損傷進展が(不安定性変数が使用されている場合は、この変数も)計算されます。その場合、fct_IDElを通じて要素サイズスケーリングが定義されていると、初期要素サイズの代わりに、最大非局所長さパラメータLE_MAXが使用されます。また、“1ステップ”の損傷フィールド初期化で非局所正則化を使用することもできます。図 6. 自動車のDP450鋼材で/FAIL/SYAZWANと組み合わせた/NONLOCAL/MATオプションの例