/FAIL/LAD

この破壊モデルは直交異方性ソリッドと厚肉シェルに対して使用可能で、Plyxfemと共にシェルプロパティ/PROP/TYPE17で積層間材料破壊モデルとしても使用できます。この破壊モデルは/MAT/LAW12 (3D_COMP)、/MAT/LAW14 (COMPSO)および/MAT/LAW25 (COMPSH)および/MAT/LAW1 (ELAST)（Plyxfemと使用される場合のみ）と適合します。

フォーマット

(1)	(2)	(3)	(5)	(7)	(9)
/FAIL/LAD_DAMA/`mat_ID`/`unit_ID`
`K`₁		`K`₂	`K`₃	$γ_{1}$	$γ_{2}$
$Y_{0}$		$Y_{c}$	`k`	`a`	$τ_{\max}$
`I`_{fail_sh}	`I`_{fail_so}

オプションの行

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fail_ID`

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位識別子。（整数、最大10桁）
`K`₁	方向1の層間剛性。デフォルト = 10³⁰（実数）	$[\frac{P a}{m}]$
`K`₂	方向2の層間剛性。デフォルト = 10³⁰（実数）	$[\frac{P a}{m}]$
`K`₃	方向3の層間剛性。デフォルト = 10³⁰（実数）	$[\frac{P a}{m}]$
$γ_{1}$	剥離モードIとモードIIの間の連成係数。デフォルト = 0（実数）
$γ_{2}$	剥離モードIとモードIIIの間の連成係数。デフォルト = 0（実数）
$Y_{0}$	剥離を開始するための降伏エネルギー損傷。デフォルト = 10³⁰（実数）
$Y_{c}$	完全な剥離のための臨界エネルギー損傷パラメータ。デフォルト = $2 \sqrt{Y_{0}}$ （実数）
`k`	亀裂伝播の速度時間定数。デフォルト = 0（実数）	$[\frac{m}{s}]$
`a`	亀裂伝播の速度倍率。デフォルト = 10³⁰（実数）
$τ_{max}$	動的緩和。 3 デフォルト = 10³⁰（実数）	$[s]$
`I`_{fail_sh}	シェル破壊フラグ。 = 1（デフォルト）損傷基準に１つの層が達するとシェルが削除されます。 = 2 損傷基準にシェルの全層が達するとシェルが削除されます。（整数）
`I`_{fail_so}	ソリッド破壊フラグ。 = 1（デフォルト）損傷基準に１つの積分点が達するとソリッドが削除されます。 = 3 損傷がソリッドの１つの積分点（ $σ_{33} = σ_{23} = σ_{13} = 0$ ）に達すると、面外応力が0に設定されます。（整数）
`fail_ID`	破壊基準識別子。 2 （整数、最大10桁）

例（複合材）

#RADIOSS STARTER
/UNIT/1
unit for mat and failure
#              MUNIT               LUNIT               TUNIT
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/COMPSH/1/1
composite example
#              RHO_I
             .001506
#                E11                 E22                NU12     Iform                           E33
              144000               10000                 .25         0                         20000
#                G12                 G23                 G31              EPS_f1              EPS_f2
                4200                4200                4200                   0                   0
#             EPS_t1              EPS_m1              EPS_t2              EPS_m2                dmax
                   0                   0                   0                   0                   0
#              Wpmax               Wpref      Ioff                         ratio
             1000000                   0         0                             0
#                  b                   n                fmax
                   0                   0             1000000
#            sig_1yt             sig_2yt             sig_1yc             sig_2yc               alpha
               10100               10100               10100               10100                   0
#           sig_12yc            sig_12yt                c_12          Eps_rate_0       ICC
               10068               10068                   0                   0         0
#          GAMMA_ini           GAMMA_max               d3max
                   0                   0                   0
#  Fsmooth                Fcut
         0                   0
/FAIL/LAD_DAMA/1/1
#                 K1                  K2                  K3              Gamma1              Gamma2
                2000                2000                2000               1E-20               1E-20
#                 Y0                  YC                   K                   A             Tau_max
                  40                 160              100000                   1                 .01
# Ifail_sh  Ifail_so                                                                               
         1         3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

剥離用のLadeveze破壊損傷モデル：(1)
$Y_{d_{3}} = {\frac{\partial E_{D}}{\partial d_{3}} |}_{σ = cst} = \frac{1}{2} \frac{{〈 σ_{33} 〉}^{2}}{K_{3} {(1 - d_{3})}^{2}} Mode I$
(2)
$Y_{d_{1}} = {\frac{\partial E_{D}}{\partial d_{1}} |}_{σ = cst} = \frac{1}{2} \frac{{σ_{31}}^{2}}{K_{1} {(1 - d_{1})}^{2}} Mode II$
(3)
$Y_{d_{2}} = {\frac{\partial E_{D}}{\partial d_{2}} |}_{σ = cst} = \frac{1}{2} \frac{{σ_{32}}^{2}}{K_{2} {(1 - d_{2})}^{2}} Mode III$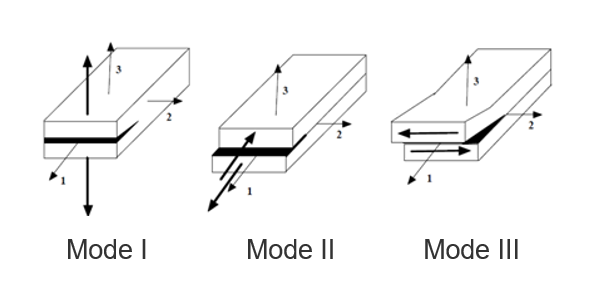

図 1.
²

2次元ソリッド要素の場合は、モードIIとモードIIIのみを使用可能です。

ここで、 $d_{i}$ はその破壊モードに伴う内部損傷パラメータです。

ダメージ進展則は等価なダメージエネルギー解放比によってコントロールされます。

$Y = Y_{d_{3}} + γ_{1} Y_{d_{1}} + γ_{2} Y_{d_{2}}$ ここで、 $Y_{d_{i}} |_{t} = \sup Y_{d_{i}} |_{τ \leq t}$

損傷パラメータの進展は連成係数 $γ_{1}$ と $γ_{2}$ に強く連成します。これらの2つのパラメータは剥離試験から来ます。

現在の破壊モデルについて、 $d_{1} = d_{2} = d_{3} = d$ であるとみなします。

損傷値dは特定の速度で増大します：(4)
$\dot{d} = \frac{k}{a} [1 - \exp (- a 〈 w (Y) - d 〉)]$

$d < 1$ の場合。

それ以外の場合は、 $d = 1$

このとき、

$a$ は、延性破壊の尺度です。値が低いほど、破壊の延性が強くなります。

$\frac{a}{k}$ は、最小破壊期間です。 $Y_{0}$ と $Y_{c}$ の間のエネルギーの期間は少なくとも $\frac{a}{k}$ に等しくなければなりません。(5)
$〈 x 〉 = {\begin{matrix} x if x > 0 \\ 0 if x < 0 \end{matrix}$

関数 $w (Y)$ は次のように計算されます：(6)
$w (Y) = \frac{〈 \sqrt{Y} - \sqrt{Y_{0}} 〉}{\sqrt{Y_{c}} - \sqrt{Y_{0}}}$

損傷パラメータ $d \leq 1.0$ ,の場合は、応力 $σ_{33}$ 、 $σ_{13}$ および $σ_{23}$ は次の関数に従って減少します：

緩和のテクニックが応力を徐々に減少させるために使用されます：(7)
$σ (t) = f (t) \cdot σ_{d} (t_{r})$

ここで、(8)
$f (t) = \exp (- \frac{t - t_{r}}{τ_{\max}}) and t \geq t_{r}$

ここで、

$t$

時間

$t_{r}$

損傷基準が推定される場合における緩和の開始時間

$τ_{max}$

動的緩和の時間

$σ_{d} (t_{r})$

損傷開始時の応力
fail_IDは、/STATE/BRICK/FAILおよび/INIBRI/FAILで使用されます。デフォルト値はありません。この行が空白の場合、/INIBRI/FAIL内の破壊モデル変数のために出力される値はありません（/STATE/BRICK/FAILオプションで.staファイルに書き込まれます）。
破壊基準に達した後、 $τ_{\max}$ の値は破断要素での応力が徐々に減少して0になるまでの期間を決定します。応力が破壊の開始時における応力値の1%に達すると、要素は削除されます。これは、要素が突然削除され、隣接要素で破断の“連鎖反応“が起こることによる不安定性を回避するために必要となります。破壊基準に達した場合でも、 $τ_{\max} = 1.0 E 30$ のデフォルト値であれば要素は削除されません。したがって、 $τ_{\max}$ をシミュレーションの時間ステップの10倍大きく定義することが推奨されます。

/FAIL/LAD_DAMA

フォーマット

定義

例（複合材）

コメント