/FAIL/INIEVO
ブロックフォーマットキーワード この基準では、2ステップの破壊アプローチを使用できます。このアプローチは、損傷が応力計算に影響を与えない開始フェーズと、応力軟化が生成される可能性のある損傷進展フェーズに分かれます。開始は、いくつかの応力状態量の関数としての塑性ひずみに基づきます。
開始基準に達すると、応力軟化損傷変数の進展が開始されます。この進展は、破壊時の塑性変位に基づくか、破壊エネルギーの特定の値に基づくことができます。さらに、形状として、従来の線形応力低減または耐荷力の指数関数的低減のどちらかを選択できます。開始 / 進展基準の複数のペアを同じ入力カードで組み合わせることができます。この基準は、ソリッドとシェルの両方に適合しており、非局所正則化と共に使用できます。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /FAIL/INIEVO/mat_ID/unit_ID | |||||||||
| NINIEVO | ISHEAR | ILEN | FAILIP | PTHICKFAIL | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| INITYPE | EVOTYPE | EVOSHAP | COMPTYP |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| TAB_ID | SR_REF | FSCALE | PARAM | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| TAB_EL | EL_REF | ELSCAL | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DISP | ALPHA | ENER | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fail_ID |
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| mat_ID | 材料識別子 (整数、最大10桁) |
|
| unit_ID | (オプション)単位の識別子。 (整数、最大10桁) |
|
| NINIEVO | 開始 / 進展基準の数。 デフォルト = 1(整数) |
|
| ISHEAR | 横せん断成分を考慮するためのフラグ(シェル専用)。
(整数) |
|
| ILEN | 要素特性長定式化のフラグ。
(整数) |
|
| FAILIP | ソリッド要素の削除が開始される破壊積分点の数。 デフォルト = 1(整数) |
|
| PTHICKFAIL | シェル要素の削除が開始される破壊層のパーセンテージ。 0.0 ≤ PTHICKFAIL ≤ 1.0 デフォルト = 0.0(実数) |
|
| INITYPE | 損傷開始の表形式基準タイプ。 2
(整数) |
|
| EVOTYPE | 損傷進展タイプ。
(整数) |
|
| EVOSHAP | 損傷進展の形状。
(整数) |
|
| COMPTYP | 基準組み合わせタイプ(NINIEVO > 0の場合のみ)。
(整数) |
|
| TAB_ID | 破壊開始基準テーブルの識別子。 (整数) |
|
| SR_REF | テーブル識別子の参照ひずみ速度。 デフォルト = 1.0(実数) |
[1s] |
| FSCALE | 破壊開始基準テーブルのスケールファクター。 デフォルト = 1.0(実数) |
|
| PARAM | 破壊開始基準のパラメータ。
デフォルト = 0.0(実数) |
|
| TAB_EL | 破壊開始基準の要素サイズスケーリング。 (整数) |
|
| EL_REF | サイズスケーリングテーブルの参照要素サイズ。 デフォルト = 1.0(実数) |
[m] |
| ELSCAL | 要素サイズスケーリング関数のスケールファクター。 デフォルト = 1.0(実数) |
|
| DISP | 破壊時の塑性変位。 デフォルト = 0.0(実数) |
[m] |
| ALPHA | 指数関数的形状パラメータ(指数関数的エネルギーベースの進展には適用できません)。 デフォルト = 1.0 |
|
| ENER | 破壊エネルギー。 デフォルト = 0.0 |
[Jm2] |
| fail_ID | (オプション)破壊基準識別子。 (整数、最大10桁) |
コメント
- INIEVO破壊基準は、塑性ひずみと応力状態に基づいた2ステップの破壊基準です。これら2つのステップは、2つの連続する損傷変数の計算で構成されます:
- 第1ステップ: 損傷開始フェーズ。示されたωD内部変数の進展が計算されます。この変数は、応力計算に影響を与えない純粋に内部的な値です。この開始変数が1.0という値に達すると、 D で表される損傷変数進展の計算によって、破壊の第2ステージが開始されます。
- 第2ステップ:損傷変数 D の進展が計算され、要素が完全に破壊して削除されるまで、応力軟化効果が生じます。
- INITYPEパラメータの値に応じて、さまざまなタイプの破壊開始基準を使用できます。
- INITYPE = 1の場合:応力軸性(オプションで、ひずみ速度)に関する表形式の破壊開始時塑性ひずみのマップが提供されます。
εinitp=f(η,˙ε)withη=−pσVM
ここで、- p
- 静水圧 −Tr(σ)/3
- σVM
- フォンミーゼス応力
- INITYPE = 2の場合:せん断の影響変数(オプションで、ひずみ速度)に関する表形式の破壊開始時塑性ひずみのマップが提供されます。
εinitp=f(θ,˙ε)withθ=σVM+kspτ
ここで、- ks
- 圧力の影響パラメータ
- τ
- 最大せん断応力
- INITYPE = 3の場合:主ひずみ速度比率(オプションで、ひずみ速度)に関する表形式の破壊開始時修正塑性ひずみのマップが提供されます。この開始基準はMSFLDとも表されます。
εinitp=f(α,˙ε)withα=˙εpminor˙εpminor≈sminorsmajor
ここで、 si は、主偏差応力成分です。
- INITYPE = 4の場合:主ひずみ速度比率(オプションで、ひずみ速度)に関する表形式の破壊開始時塑性ひずみのマップが提供されます。この開始基準はFLDとも表されます。
εinitp=f(α,˙ε)withα=˙εpminor˙εpminor≈sminorsmajor
- INITYPE = 5の場合:
β
と表される応力状態パラメータ(オプションで、ひずみ速度)に関する表形式の破壊開始時塑性ひずみのマップが提供されます。この開始基準はFLDとも表されます。εinitp=f(β,˙ε)withβ=σVM+kdpσmajor重要: 破壊基準に適用されるひずみ速度依存性は、ひずみ速度に依存する材料則のみで使用できます。構成則に使用されるひずみ速度(全ひずみ速度、偏差ひずみ速度、または塑性ひずみ速度)は、破壊基準に使用されるのと同じものになります。
- INITYPE = 1の場合:応力軸性(オプションで、ひずみ速度)に関する表形式の破壊開始時塑性ひずみのマップが提供されます。
- 損傷開始変数
ωD
は、次のように増分的に計算されます:
(1) ωD=∞∑t=0Δεpεinitp- INITYPE = 3(MSFLD)の場合は、修正塑性ひずみが使用され、このひずみは
η>0
の場合にのみ進展します:
(2) ωD=∞∑t=0Δεpεinitp - INITYPE = 3(MSFLD)およびINITYPE = 4(FLD)基準の場合は、PARAMの値に応じて、増分定式化の代わりに直接定式化を使用できます:
(3) ωD=εpεinitp
- INITYPE = 3(MSFLD)の場合は、修正塑性ひずみが使用され、このひずみは
η>0
の場合にのみ進展します:
- 要素サイズの正則化を考慮するために、初期要素サイズ
Le
に関するマップ
fsize
として表される要素サイズのスケールファクターを記述するテーブル(TAB_EL)を定義できます。また、オプションで、INITYPEの値に応じて破壊開始基準に応力状態変数を使用することもできます。例えば、INITYPE = 2の場合、
fsize=f(Le,θ)
となります。要素サイズ係数は、次のように損傷開始変数の計算に導入されます:
(4) ωD=∞∑t=0Δεpεinitp⋅fsize - 損傷開始変数
ωD
が1という値に達すると、損傷変数の進展
D
が開始され、応力軟化が生じます。この進展は、次のいずれかに基づくことができます:
- EVOTYPE = 1の場合、ufp と表される破壊時の塑性変位(DISP)。
- EVOTYPE = 2の場合、Gf と表される消散破壊エネルギー(ENER)。
- EVOSHAPパラメータを使用すると、損傷進展の形状を定義できます。両方の進展タイプについて(塑性変位または破壊エネルギー)、線形形状と指数関数的形状を選択できます。
- EVOSHAP = 1の場合、損傷進展は線形です:
- EVOTYPE = 1の場合: 破壊時の塑性変位はDISPで直接入力されます。
(5) ΔD=LeΔεpufpここで、Le は初期要素長です。図 1. 破壊時の塑性変位DISPによる線形損傷の進展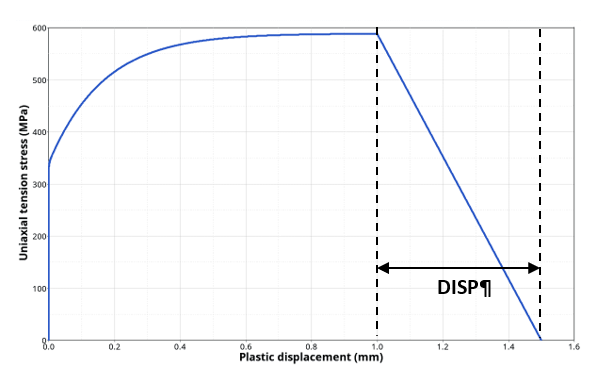
- EVOTYPE = 2の場合: 破壊時の塑性変位は、ENERを使用して計算される破壊エネルギー入力から求められます。
ΔD=LeΔεpufpwithufp=2Gfσ0Y
ここで、 σ0Y は、損傷進展開始時の降伏応力です。注: この式では、消散エネルギーが Gf と等しくなるように、損傷の開始時に塑性挙動がほぼ完全であると見なされます。図 2. 破壊エネルギー入力ENERによる線形の損傷進展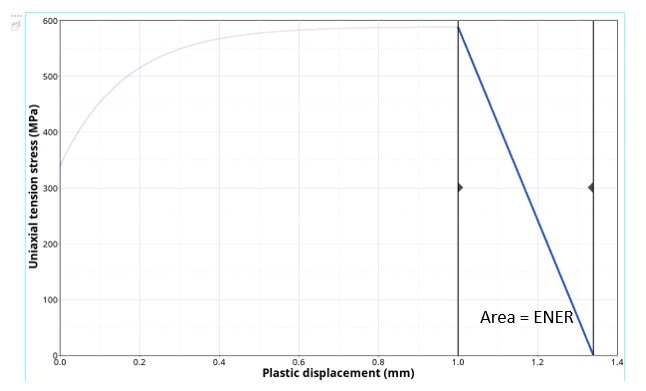
- EVOTYPE = 1の場合: 破壊時の塑性変位はDISPで直接入力されます。
- EVOSHAP = 2の場合、損傷進展は指数関数的です。
- EVOTYPE = 1の場合: 破壊時の塑性変位はDISPで直接入力され、指数関数の形状はALPHAを使用して変更できます。
(6) D=1−e−αLe(εp−ε0p)ufp1−e−α図 3. 塑性変位DISPによる指数関数的な損傷進展. さまざまなアルファパラメータ値を使用した破壊時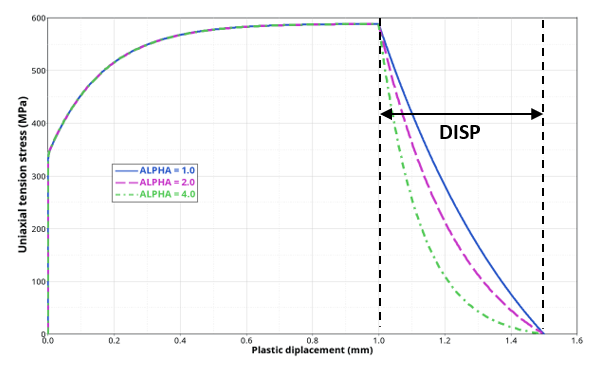
- EVOTYPE = 2の場合: 指数関数の応力-塑性変位曲線とx軸との間の面積は、破壊エネルギーENERに相当します。
D=1−e−EdisGfwithEdis=D=1∫D=0σY⋅LeΔεp
図 4. 破壊エネルギー入力ENERによる指数関数的な損傷進展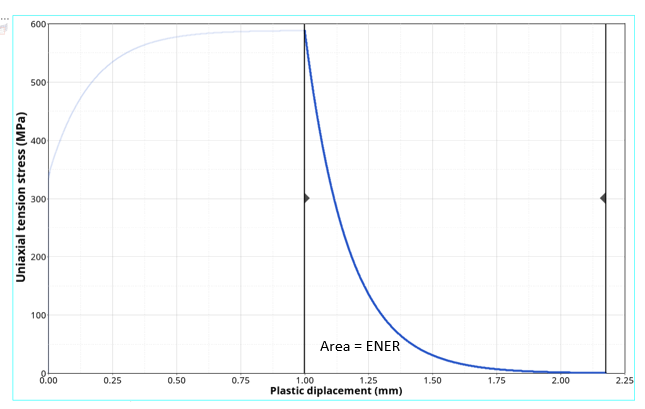
- EVOTYPE = 1の場合: 破壊時の塑性変位はDISPで直接入力され、指数関数の形状はALPHAを使用して変更できます。
- EVOSHAP = 1の場合、損傷進展は線形です:
- 同じ材料について、複数の開始 / 進展基準ペアを同じ入力カード内で定義して、NINIEVO > 1という値を設定できます。この場合、別のパラメータCOMPTYPを使用して、軟化効果を生じさせるためにさまざまな基準をどのように組み合わせるのかを選択できます。
- COMPTYP = 1の場合: Di
で表される対象の基準の損傷変数は、COMPTYP = 1を使用しているすべての基準の間での最大値と比較されます。
DMAX=max(Di,DMAX)withi∈NMAX
ここで、NMAX は、COMPTYP = 1を使用している開始 / 進展カードの数です。
- COMPTYP = 2の場合:
Di
で表される対象の基準の損傷変数は、COMPTYP = 2を使用しているすべての基準の間で乗法式によって累積されます。
(7) DMULT=1−∏i∈Nmult(1−Di)ここで、 NMULT は、COMPTYP = 2を使用している開始 / 進展カードの数です。
最後に、損傷応力テンソルを計算するために使用される全体損傷変数は、次の最大値として定義されます:(8) D=max(DMAX,DMULT)σ=(1−D)σeffここで、- σ
- 最終的な損傷応力テンソル
- σeff
- 有効応力テンソル(塑性リターンマッピング後に材料則から得られます)
- COMPTYP = 1の場合: Di
で表される対象の基準の損傷変数は、COMPTYP = 1を使用しているすべての基準の間での最大値と比較されます。
- FAILIPは、高次または完全積分ソリッド要素にのみ使用される整数値です。これは、ソリッド要素の削除が開始される破壊積分点の数を定義します。
- PTHICKFAILパラメータは、シェル要素に使用される実数パラメータです。PTHICKFAILが空白であるか、0.0に設定されている場合、シェルプロパティのPTHICKFAILの値が使用されます。PTHICKFAIL > 0.0の場合、シェルプロパティで定義されたPTHICKFAILの値は無視され、この破壊モデルに入力された値が使用されます。PTHICKFAIL > 0.0の値の場合、板厚方向の破壊積分点の比率がPTHICKFAIL以上になると、シェル要素が破壊されて削除されます。
- ILENは、要素の特性長
Le
を計算するための2つの式の候補からいずれかを選択するためのフラグパラメータです。
- ILEN=0
- 初期形状定式化です。ここでは、特性長は、シェルの初期面積の平方根に相当し(Le=√A0 )、ソリッドの初期体積の立方根に相当します(Le=3√V0 )。
- ILEN = 1
- 初期限界時間ステップ定式化です。ここでは、特性長は、初期要素限界時間ステップを計算するために使用される特性長に相当します。使用される式は、シェルまたはソリッドのさまざまな定式化の間で異なる可能性があります。
- ILEN = 2
- 現在の形状定式化です。ここでは、特性長は、シェルの現在の面積の平方根に相当します(Le=√A )。
- 非局所正則化が使用されている場合(/NONLOCAL/MAT)、非局所塑性ひずみを使用して、損傷開始変数と損傷変数が計算されます(不安定性変数が使用されている場合は、この変数も計算されます)。また、この場合、すべての式の初期要素長 Le は、非局所パラメータ LMAX に置き換えられます。