/MAT/LAW104 (JOHNS_VOCE_DRUCKER)

ブロックフォーマットキーワード Voce硬化と線形硬化が混在する6次Druckerモデルを使用した弾塑性材料構成則。Johnson-Cookひずみ速度の依存性および自己加熱に起因する熱軟化の効果もモデル化できます。この構成則は、等方性のシェル要素およびソリッド要素に適用できます。

フォーマット

(1)	(3)	(5)	(7)	(9)
/MAT/LAW104/`mat_ID`/`unit_ID` または /MAT/JOHNS_VOCE_DRUCKER/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$v$	`I`_res
$σ_{y l d}^{0}$	`H`	`Q`	`B`	`C`_DR
`C`_JC	${\dot{ε}}_{0}$
$μ$	`T`_ref	`T`_ini
$η$	`C`_p	${\dot{ε}}_{i s o}$	${\dot{ε}}_{a d}$

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位の識別子（オプション）（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`	ヤング率。（実数）	$[Pa]$
$v$	ポアソン比。（実数）
`I`_res	塑性の解法。 = 0 1に設定 = 1（デフォルト） NICE（Next Increment Correct Error）陽解法。 = 2 Newton反復陰解法。（整数）
$σ_{y l d}^{0}$	初期降伏応力（実数）	$[Pa]$
`H`	線形硬化モジュール。（実数）	$[Pa]$
`Q`	Voce硬化係数（実数）	$[Pa]$
`B`	Voce硬化指数。（実数）
`C`_DR	Drcker係数。（実数）
`C`_JC	Johnson-Cookひずみ速度係数。（実数）
${\dot{ε}}_{0}$	塑性ひずみ速度の非粘性極限。（実数）	$[\frac{1}{s}]$
$μ$	温度軟化曲線。（実数）	$[\frac{1}{K}]$
`T`_ref	実験で硬化則が確認された基準温度。（実数）	$[K]$
`T`_ini	シミュレーションにおける材料の初期温度。（実数）	$[K]$
$η$	Taylor-Quinney係数。（実数）
`C`_p	比熱（実数）	$[\frac{J}{kg \cdot K}]$ .
${\dot{ε}}_{i s o}$	等温条件における塑性ひずみ。（実数）	$[\frac{1}{s}]$
${\dot{ε}}_{a d}$	断熱条件における塑性ひずみ。（実数）	$[\frac{1}{s}]$

この構成則では、次のように6次のDrucker相当応力定義を使用しています。 (1)
$σ_{e q} = k {(J_{2}^{3} - C_{D R} J_{3}^{2})}^{\frac{1}{6}}$

$J_{2}$ と $J_{3}$ は、それぞれ偏差応力テンソル $k = {(\frac{1}{27} - C_{D R} \frac{4}{27^{2}})}^{- \frac{1}{6}}$ の第2不変量と第3不変量です。

このパラメータはユーザー定義であり、複数の降伏曲面を定義できます（図 1）。この図にある凸性を考慮するには、このパラメータ値を-27/8 ≤ C_DR ≤ 2.25の範囲で指定する必要があります。

図 1. Drucker降伏曲面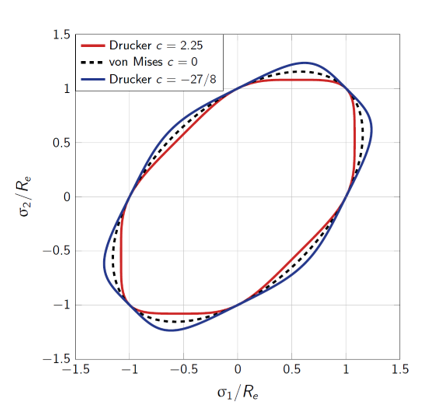
降伏関数を次のように定義します。(2)
$ϕ = \frac{σ_{e q}^{2}}{σ_{y l d}^{2}} - 1 = 0$

および (3)
$σ_{y l d} = (σ_{y l d}^{0} + H ε_{p} + Q (1 - e^{- B ε_{p}})) (1 + C_{J C} ln (\frac{{\dot{ε}}_{f}}{{\dot{ε}}_{0}})) (1 - μ (T - T_{r e f}))$

ここで、

$σ_{y l d}^{0}$

初期降伏応力

H

線形硬化。

$Q, B$

Voce硬化パラメータ。

$C_{J C}$

Johnson-Cookひずみ速度係数。

${\dot{ε}}_{f}$

フィルターつき塑性ひずみ速度。

ユーザーズガイドのフィルタリングをご参照ください。

${\dot{ε}}_{0}$

非粘性極限塑性ひずみ速度。

$μ$

熱軟化曲線。

塑性に対するこの流れ応力方程式の変化。

図 2. 塑性に対する流れ応力の変化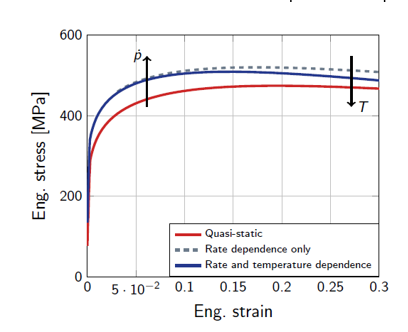
この材料に/HEAT/MATを使用していない場合、次の増分式を使用して温度が内部的に計算されます。(4)
$d T = ω ({\dot{ε}}_{p}) \frac{η}{C_{p}} d W_{p}$

ここで、

$d W_{p}$

塑性ひずみエネルギーの増分。

$η$

考慮を必要とするTaylor-Quinney係数 $0 \leq η \leq 1$ 。

$ω ({\dot{ε}}_{p})$

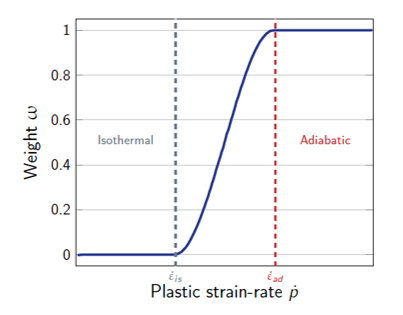
等温条件と断熱条件間の遷移を定義する係数（図 3）。

(5)
$ω (\dot{ε_{p}}) = \frac{{({\dot{ε}}_{p} - {\dot{ε}}_{i s o})}^{2} (3 {\dot{ε}}_{a d} - 2 {\dot{ε}}_{p} - {\dot{ε}}_{i s o})}{{({\dot{ε}}_{a d} - {\dot{ε}}_{i s o})}^{3}}$

図 3. 塑性ひずみ速度に対する温度重みの変化

/MAT/LAW104 (JOHNS_VOCE_DRUCKER)

フォーマット

定義

コメント