/MAT/LAW53 (TSAI_TAB)

ブロックフォーマットキーワード一方向直交異方性弾塑性材料則の法則を記述します。これは、ソリッド要素でのみ使用されます。

フォーマット

(1)	(2)	(3)	(4)	(5)	(7)	(9)
/MAT/LAW53/`mat_ID`/`unit_ID`または/MAT/TSAI_TAB/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`₁₁		`E`₂₂
`G`₁₂		`G`₂₃
`fct_ID`₁₁	`fct_ID`₂₂	`fct_ID`₁₂	`fct_ID`₂₃	`fct_ID`₄₅
`Fscale`₁₁		`Fscale`₂₂		`Fscale`₁₂	`Fscale`₂₃	`Fscale`₄₅

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位識別子（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`₁₁	ヤング率（実数）	$[Pa]$
`E`₂₂	ヤング率（実数）	$[Pa]$
`G`₁₂	せん断係数（実数）	$[Pa]$
`G`₂₃	せん断係数（実数）	$[Pa]$
`fct_ID`₁₁	方向11における降伏応力関数の識別子（整数）
`fct_ID`₂₂	方向22における降伏応力関数の識別子（整数）
`fct_ID`₁₂	方向12における降伏応力関数の識別子（整数）
`fct_ID`₂₃	方向23における降伏応力関数の識別子（整数）
`fct_ID`₄₅	方向45における降伏応力関数の識別子（整数）
`Fscale`₁₁	降伏関数11のスケールファクターデフォルト = 1.0（実数）	$[Pa]$
`Fscale`₂₂	降伏関数22のスケールファクターデフォルト = 1.0（実数）	$[Pa]$
`Fscale`₁₂	降伏関数12のスケールファクターデフォルト = 1.0（実数）	$[Pa]$
`Fscale`₂₃	降伏関数23のスケールファクターデフォルト = 1.0（実数）	$[Pa]$
`Fscale`₄₅	降伏関数45のスケールファクターデフォルト = 1.0（実数）	$[Pa]$

例（プラスチック）

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                 Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW53/1/1
plastic
#              RHO_I
               2E-10
#                E11                 E22
                 200                 200
#                G12                 G23
                 100                 100
# fct_ID11  fct_ID22  fct_ID12  fct_ID23  fct_ID45
         1         1         3         4         5
#           Fscale11            Fscale22            Fscale12            Fscale23            Fscale45
                   0                   0                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
function_1
#                  X                   Y
                   0                 200                                                           
                  .1                 200                                                           
                 .11                 100                                                           
                  .5                 100                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
function_2
#                  X                   Y
                   0                   1                                                           
               10000                   1                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3
function_3
#                  X                   Y
                   0                 200                                                           
                  .1                 200                                                           
                 .11                 100                                                           
                  .5                 100                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/4
function_4
#                  X                   Y
                   0                 200                                                           
                  .5                 200                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/5
function_5
#                  X                   Y
                   0                 100                                                           
                  .5                 100                                                           
                 1.5               20000                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

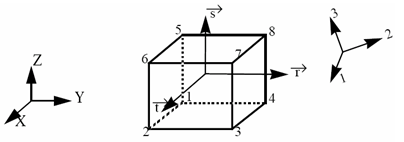
直交異方性参照フレーム（1、2、3）は、各有限要素の当該プロパティセットで定義されます。
ソリッドプロパティセット（/PROP/TYPE14）では、I_solid = 1、2、または2の場合に全体フレームが使用されます。

図 1.
全体フレームは、( $X$ , $Y$ , $Z$ )です。

局所フレームは、(

t

r

s

)です。

$σ_{11} = E_{11} ε_{11}$	$σ_{12} = G_{12} ε_{12}$
$σ_{22} = E_{22} ε_{22}$	$σ_{23} = G_{23} ε_{23}$
$σ_{33} = E_{33} ε_{33}$	$σ_{13} = G_{13} ε_{13}$

この材料則は直交異方性で、E₃₃ = E₂₂およびG₁₃ = G₁₂です。
降伏サーフェスはTSAI-WU降伏基準です：(1)
$\begin{array}{l} F = F_{1} σ_{11} + F_{2} σ_{22} + F_{2} σ_{33} + F_{11} σ_{11}^{2} + F_{22} σ_{22}^{2} + F_{22} σ_{33}^{2} \\ + F_{44} σ_{12}^{2} + F_{55} σ_{23}^{2} + F_{44} σ_{13}^{2} + 2 F_{12} σ_{11} σ_{22} + 2 F_{23} σ_{22} σ_{33} \\ + 2 F_{12} σ_{11} σ_{33} \end{array}$

ここで、 (2)
$\begin{matrix} F_{1} = - \frac{1}{σ_{1 y}^{c}} + \frac{1}{σ_{1 y}^{t}}; & F_{2} = - \frac{1}{σ_{2 y}^{c}} + \frac{1}{σ_{2 y}^{t}} \end{matrix}$
(3)
$\begin{matrix} F_{11} = \frac{1}{σ_{1 y}^{c} σ_{1 y}^{t}}; & F_{22} = \frac{1}{σ_{2 y}^{c} σ_{2 y}^{t}}; & F_{44} = \frac{1}{σ_{4 y}^{c} σ_{4 y}^{t}}; & F_{55} = \frac{1}{σ_{5 y}^{c} σ_{5 y}^{t}} \end{matrix}$
(4)
$\begin{matrix} F_{12} = - \frac{1}{2} \sqrt{F_{11} F_{22}}; & F_{23} = - \frac{1}{2} F_{22} \end{matrix}$

パラメータ： $σ_{1 y}^{c}, σ_{1 y}^{t}, σ_{2 y}^{c}, σ_{2 y}^{t}, σ_{4 y}^{c}, σ_{4 y}^{t}, σ_{5 y}^{c}, σ_{5 y}^{t}$ は変数で、降伏関数によって導出されます。
fct_ID₄₅ ≠ 0の場合、(5)
$F_{12} = \frac{2}{σ_{45 y}^{2}} - \frac{1}{2} (F_{11} + F_{22} + F_{44}) + \frac{F_{1} + F_{2}}{σ_{45 y}^{c}}$

/MAT/LAW53 (TSAI_TAB)

フォーマット

定義

例（プラスチック）

コメント