/MAT/LAW93 (ORTH_HILL)または(CONVERSE)

ブロックフォーマットキーワードこの材料則はHill塑性を擁する直交異方性弾性挙動材料を記述し、シェルおよびソリッド要素に適用可能です。（/BRICK、/TETRA4および/TETRA10）。

シェル要素の場合はプロパティセット/PROP/TYPE11、/PROP/TYPE17、/PROP/TYPE51、/PROP/PCOMPP、ソリッド要素の場合は/PROP/TYPE6と使用されます。

フォーマット

(1)	(2)	(3)	(5)	(7)	(9)
/MAT/LAW93/`mat_ID`/`unit_ID`または/MAT/ORTH_HILL/`mat_ID`/`unit_ID`または/MAT/CONVERSE/`mat_ID`/`unit_ID`/
`mat_title`
$ρ_{i}$
`E`₁₁		`E`₂₂	`E`₃₃	`G`₁₂	$ν_{12}$
`G`₁₃		`G`₂₃	$ν_{13}$	$ν_{23}$
`N`_rate	`VP`	`F`_cut

N_{r a t e} > 0

の場合の降伏の曲線入力、行毎にN_rate 塑性関数を定義：

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fct_ID`_i		`Fscale`_i		${\dot{ε}}_{i}$

降伏のパラメータ入力：

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$σ_{y}$		`QR`₁		`CR`₁		`QR`₂		`CR`₂

HILL基準の降伏応力比：

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`R`₁₁		`R`₂₂		`R`₁₂
`R`₃₃		`R`₁₃		`R`₂₃

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位識別子。（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`₁₁	方向11のヤング率（実数）	$[Pa]$
`E`₂₂	方向22のヤング率（実数）	$[Pa]$
`E`₃₃	方向33のヤング率（実数）	$[Pa]$
`G`₁₂	方向12におけるせん断係数（実数）	$[Pa]$
`G`₁₃	方向13におけるせん断係数（実数）	$[Pa]$
`G`₂₃	方向23におけるせん断係数（実数）	$[Pa]$
$ν_{12}$	ポアソン比12 （実数）
$ν_{13}$	ポアソン比13 （実数）
$ν_{23}$	ポアソン比23 （実数）
`N`_rate	降伏関数の数
`VP`	ひずみ速度選択フラグ = 1 降伏応力に対するひずみ速度効果は塑性ひずみ速度に依存します。 = 2（デフォルト）降伏に対するひずみ速度効果は全ひずみ速度に依存します。 = 3 降伏に対するひずみ速度効果はひずみ速度の偏差に依存します。（整数）
`F`_cut	ひずみ速度フィルタリングのカットオフ周波数。デフォルト = 1.0 x 10⁴（実数）	$[Hz]$
`fct_ID`_i	塑性曲線のi番目の関数の識別子（i=1、`N`_rate）（整数）
`Fscale`_i	i番目の関数のスケールファクター（i=1、`N`_rate）デフォルト = 1.0（実数）	$[Pa]$
${\dot{ε}}_{i}$	i番目の関数のひずみ速度（i=1、`N`_rate）（実数）	$[\frac{1}{s}]$
$σ_{y}$	初期降伏応力デフォルト = 1E30 （実数）	$[Pa]$
`QR`₁	硬化のパラメータデフォルト = 0.0（実数）	$[Pa]$
`CR`₁	硬化のパラメータデフォルト = 0.0（実数）
`QR`₂	硬化のパラメータデフォルト = 0.0（実数）	$[Pa]$
`CR`₂	硬化のパラメータデフォルト = 0.0（実数）
`R`₁₁	方向11の降伏応力比デフォルト = 1.0（実数）
`R`₂₂	方向22の降伏応力比デフォルト = 1.0（実数）
`R`₃₃	方向33の降伏応力比デフォルト = 1.0（実数）
`R`₁₂	方向12の降伏応力比デフォルト = 1.0（実数）
`R`₁₃	方向13の降伏応力比デフォルト = 1.0（実数）
`R`₂₃	方向23の降伏応力比デフォルト = 1.0（実数）

例（曲線入力）

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW93/1/1
plastic
#              RHO_I
           2.730E-09
#                E11                 E22                 E33                 G12                Nu12
              225654              195400              178526            75187.97                0.30
#                G13                 G23                Nu13                Nu23
            75187.97            75187.97                0.28                0.32
#     Nrate       VP                Fcut
         2         1                 0.0
#   Ifunct                        Yscale              Epsdot
         5                           1.0                0.01	     
         5                           1.5               100.0	       
#               SigY                 QR1                 CR1                 QR2                 CR2
                   0                   0                   0                 0.0                 0.0
#                R11                 R22                 R12
                 1.0             1.05626             0.96425
#                R33                 R13                 R23
              0.9337                 1.0                 1.0
/FUNCT/5
plastic
#                  X                   Y           
                   0         165.6362749
               0.002         173.8123558
               0.005         180.2967164
                0.01         186.5926709
                0.02         193.8182168
                0.05         204.4407991
                0.07         208.5903797
                 0.1         213.1182051
                0.12         215.4817557
                0.15         218.4183864
                0.17         220.0863912
                 0.2         222.2743041
                0.22         223.5689486
                0.25         225.3186882
                0.27         226.3794409
                 0.3         227.840544
                0.32         228.7406278
                0.35         229.996802
                0.37         230.7795124
                 0.4         231.8824363
                 0.5         235.0704031
                 0.6         237.7095003
                 0.7         239.9650034
                 0.8         241.9367878
                 0.9         243.689935
                   1         245.2692715
                 1.5         251.4456403
                   2         255.9237789
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

降伏応力は、直交異方性フレームの相当応力と比較されます。ソリッド要素の場合、この相当応力は次のように定義されます：(1)
$σ_{e q} = \sqrt{F (σ_{22}^{2} - σ_{33}^{2}) + G (σ_{33}^{2} - σ_{11}^{2}) + H (σ_{11}^{2} - σ_{22}^{2}) + 2 L σ_{23}^{2} + 2 M σ_{31}^{2} + 2 N σ_{12}^{2}}$

ここで、

$F = \frac{1}{2} (\frac{1}{R_{22}^{2}} + \frac{1}{R_{33}^{2}} - \frac{1}{R_{11}^{2}})$

$G = \frac{1}{2} (\frac{1}{R_{33}^{2}} + \frac{1}{R_{11}^{2}} - \frac{1}{R_{22}^{2}})$

$H = \frac{1}{2} (\frac{1}{R_{22}^{2}} + \frac{1}{R_{11}^{2}} - \frac{1}{R_{33}^{2}})$

$L = \frac{3}{2 R_{23}^{2}}$

$M = \frac{3}{2 R_{31}^{2}}$

$N = \frac{3}{2 R_{12}^{2}}$

$R_{i i}^{} = \frac{σ_{F}^{i i}}{σ_{F}}$

法線方向

$R_{i j}^{} = \frac{\sqrt{3} σ_{F}^{i j}}{σ_{F}}$

せん断方向

$σ_{F}^{i j}$

方向の降伏応力 $i j$

$σ_{F}^{}$

Voce硬化の合計で定義したり、表形式にすることができるグローバル流動応力（以下を参照）。

平面応力条件下では、シェル要素の場合、相当降伏応力は次のようになります：(2)
$σ_{e q} = \sqrt{(G + H) σ_{11}^{2} + (F + H) σ_{22}^{2} - 2 H σ_{11} σ_{22} + 2 N σ_{12}^{2}}$
降伏関数 $Φ$ は、Hillの相当応力 $σ_{e q}$ を流動応力 $σ_{F}^{}$ と次のように比較します：(3)
$Φ = σ_{e q} - σ_{F}$
流動応力 $σ_{F}^{}$ を定義する方法には異なる2つの方法があります：パラメータ入力または曲線入力です。
- パラメータ入力の場合、流応力は、初期降伏応力と二重Voce硬化を用いて次のように定義されます。(4)
  $σ_{F} = σ_{Y}^{0} + R (ε_{p})$
  
  ここで、 $R (ε_{p}) = \sum_{i}^{2} Q R_{i} \cdot (1 - e^{- C R_{i} \cdot ε_{p}})$ 。
- 曲線入力の場合、パラメータ入力の値は無視されます。
  降伏は、ひずみ速度効果を考慮し、応力対塑性ひずみ曲線を用いて定義できます。応力対ひずみ曲線が定義されている場合、これが硬化を定義するデフォルトの方法となります。
  1. $\dot{ε} \leq {\dot{ε}}_{n}$ の場合、降伏は $f_{n}$ と $f_{n - 1}$ の間で補間されます。
  2. $\dot{ε} \leq {\dot{ε}}_{1}$ の場合、関数 $f_{1}$ が使用されます。
  3. ${\dot{ε}}_{\max}$ を超えた場合、降伏は外挿されます。
    
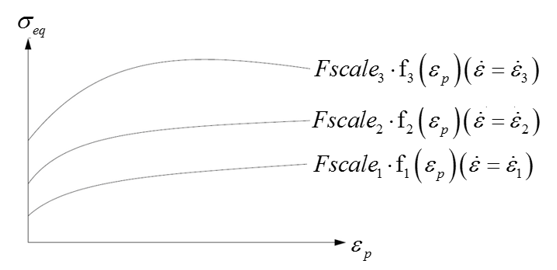
    図 1.
表形式の流動応力の場合、ひずみ速度 ε ˙ の計算はフラグVPの値に依存します。
- VP= 1の場合、塑性ひずみ速度が使用されます
- VP= 2の場合、全ひずみ速度が使用されます
- VP= 3の場合、全ひずみ速度が使用されます
すべての場合において、ひずみ速度の計算にはフィルタリングが含まれます。VP = 1の場合、カットオフ周波数が自動的に設定されます。ただし、VP = 1または3の場合、カットオフ周波数F_cutを入力できます。それ以外の場合は、デフォルト値が設定されます。

/MAT/LAW93 (ORTH_HILL)または(CONVERSE)

フォーマット

定義

例（曲線入力）

コメント