/MAT/LAW76 (SAMP)
ブロックフォーマットキーワード この材料則は、引張、圧縮、およびせん断(ひずみの関数としての応力)について、加工硬化部分にユーザー定義関数を使用して半解析的弾塑性材料を記述します。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW76/mat_ID/unit_IDまたは/MAT/SAMP/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| ρiρi | |||||||||
| E | νν | ||||||||
| tab_IDt | tab_IDc | tab_IDs | |||||||
| Fscalet | Fscalec | Fscales | XFAC | ||||||
| νpνp | fct_IDpr | Fscalepr | Fsmooth | Fcut | |||||
| εfpεfp | εrpεrp | ||||||||
| fct_ID1 | Fscale1 | ||||||||
| Iform | IQUAD | ICONV | |||||||
定義
| フィールド | 内容 | SI単位の例 |
|---|---|---|
| mat_ID | 材料識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子。 (整数、最大10桁) |
|
| mat_title | 材料のタイトル (文字、最大100文字) |
|
| ρiρi | 初期密度 (実数) |
[kgm3][kgm3] |
| E | 初期ヤング率 (実数) |
[Pa][Pa] |
| νν | ポアソン比 (実数) |
|
| tab_IDt | 引張降伏応力のテーブル識別子(ひずみ速度に依存する可能性がある場合の応力対塑性引張ひずみ) (整数) |
|
| tab_IDc | 圧縮降伏応力のテーブル識別子(ひずみ速度に依存する可能性がある場合の応力対塑性圧縮ひずみ) (整数) |
|
| tab_IDs | せん断降伏応力のテーブル識別子(ひずみ速度に依存する可能性がある場合の応力対塑性せん断ひずみ) (整数) |
|
| Fscalet | tab_IDtの縦軸(応力)のスケールファクター デフォルト = 1.0(実数) |
[Pa][Pa] |
| Fscalec | tab_IDcの縦軸(応力)のスケールファクター デフォルト = 1.0(実数) |
[Pa][Pa] |
| Fscales | tab_IDsの縦軸(応力)のスケールファクター デフォルト = 1.0(実数) |
[Pa][Pa] |
| XFAC | 3つのテーブル(tab_IDt、tab_IDc、tab_IDs)の2つ目のエントリ(ひずみ速度)のスケールファクター 6 デフォルト = 1.0(実数) |
|
| νpνp | 塑性ポアソン比 (実数) |
|
| fct_IDpr | 塑性ポアソン比関数識別子(塑性ひずみに対する
νpνp
) (実数) |
|
| Fscalepr | fct_IDprの縦軸(
νpνp
)のスケールファクター デフォルト = 1.0(実数) |
|
| Fsmooth | ひずみ速度スムージングオプションフラグ。
(整数) |
|
| Fcut | ひずみ速度フィルタリングのカットオフ周波数。 デフォルト = 1030(実数) |
[Hz][Hz] |
| εfpεfp | 破壊塑性ひずみ(要素損傷の開始) デフォルト = 2e30 (実数) |
|
| εrpεrp | 最大塑性ひずみ(要素は削除されます) デフォルト = 2e30 (実数) |
|
| fct_ID1 | 損傷関数識別子(塑性ひずみに対する損傷) 2 (整数) |
|
| Fscale1 | fct_ID1の縦軸のスケールファクター 2 デフォルト = 1.0(実数) |
|
| Iform | 定式化フラグ 4
(整数) |
|
| IQUAD | 降伏曲面フラグ 3
(整数) |
|
| ICONV | 凸性条件フラグ
(整数) |
▸例(材料)
コメント
- 材料は、シェル要素、厚肉シェル要素、およびソリッド要素と適合性があります。
- 材料の損傷は以下の2つの方法でモデル化できます:
- εfpεfp (損傷の開始)と εrpεrp (要素の削除)
- 損傷関数fct_ID1
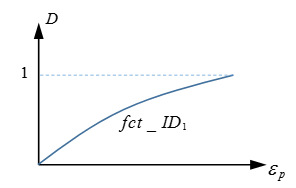
損傷関数fct_ID1が使用される場合、 εfpεfp と εrpεrp は無視されます。
- 降伏曲面は次のように選択されます:
(1) f={σVM−A0−A1P−A2P2 IQUAD=0σ2VM−A0−A 1P−A2P2 IQUAD=1 f={σVM−A0−A1P−A2P2IQUAD=0σ2VM−A0−A1P−A2P2IQUAD=1ここで、(2) P=−σxx+σyy+σzz3P=−σxx+σyy+σzz3(3) σVM=√32[(σxx+P)2+(σyy+P)2+(σzz+P)2+2σ2xy+2σ2yz+2σ2xz]σVM=√32[(σxx+P)2+(σyy+P)2+(σzz+P)2+2σ2xy+2σ2yz+2σ2xz]A0A0 、 A1A1 、 A2A2 は、引張、圧縮、およびせん断に対して定義される硬化曲線から計算されます。
von MisesおよDrucker-Prager降伏曲面については、IQUAD=0が使用できます。ただし、IQUAD=0を使用すると、Radiossが A0A0 、 A1A1 および A2A2 係数をフィットさせるのは困難な場合もあり、IQUAD=1を使用したほうがより簡単なフィットが得られます。
- 塑性定式化の選択
- 非関連流れ則の塑性については、Iform=0:
塑性流れ則関数 gg は、塑性ひずみの増分 dεp=dλ∂g∂σ を表すために使用されます。この場合、 ∂g∂σ は降伏局面に直交せず、 f と g は降伏曲面 f
図 1.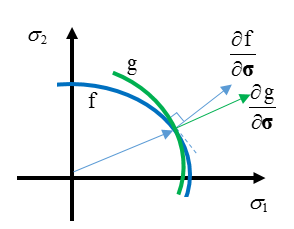 塑性流れ則、 g は次の式で与えられます:
塑性流れ則、 g は次の式で与えられます:(4) g=√σ2VM+αP2土や岩などのミネラルは通常、非関連塑性定式化 Iform=0を使用します。
- 関連流れ則の塑性に対しては: Iform= 1、
g=f
この場合、塑性ひずみ速度は降伏曲面 f の法線ベクトルの関数です。金属などの材料は通常、関連塑性定式化を使用します。
(5) dεp=dλ∂f∂σ=dλ∂g∂σ図 2.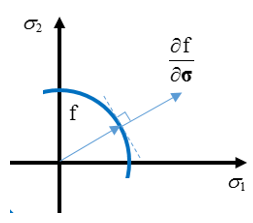
- 非関連流れ則の塑性については、Iform=0:
- 凸性条件フラグICONV=1は、降伏曲面が凸であることを確実にすることによって、材料則内の安定性を確保するために使用されます。降伏曲面は、引張と圧縮でせん断降伏応力値が低いと双曲線になり得ます。この場合、一意解は存在せず、Radiossはせん断降伏応力を更新(増加)して降伏曲面の凸性を確保します。したがって、せん断降伏応力は入力曲線と異なる場合もあります。
- テーブルは最大で2次元でなくてはなりません。最初のエントリは塑性ひずみで、2番目のエントリはひずみ速度です。
- ユーザー変数USR2、USR3、USR4を使用して、引張、圧縮、およびせん断の塑性ひずみ成分を出力します。この出力は、シェルとソリッドの両方について時刻歴とアニメーションファイルで得ることができます。